相関グラフとは？データの関係性を見抜く散布図の見方・作り方をやさしく解説

相関関係とは？基本を理解しよう

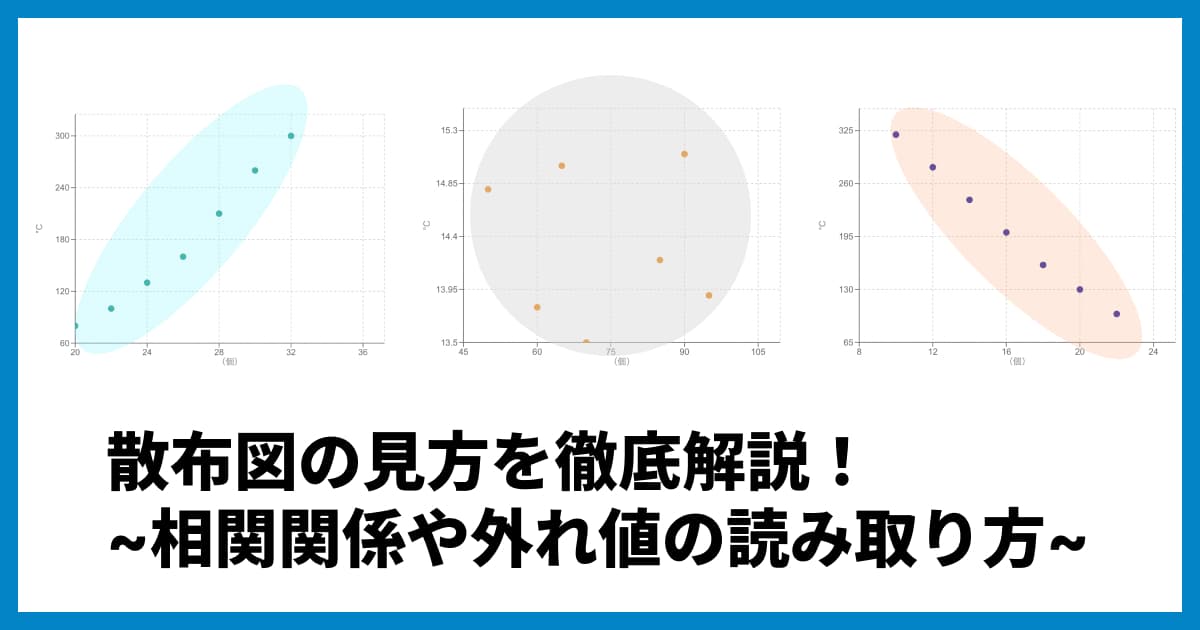
まず、「相関」とは何でしょうか？簡単に言うと、「片方が変化すると、もう片方も変化する」という、2つのデータの関係性のことです。この関係性には、大きく分けて3つのパターンがあります。

• 正の相関
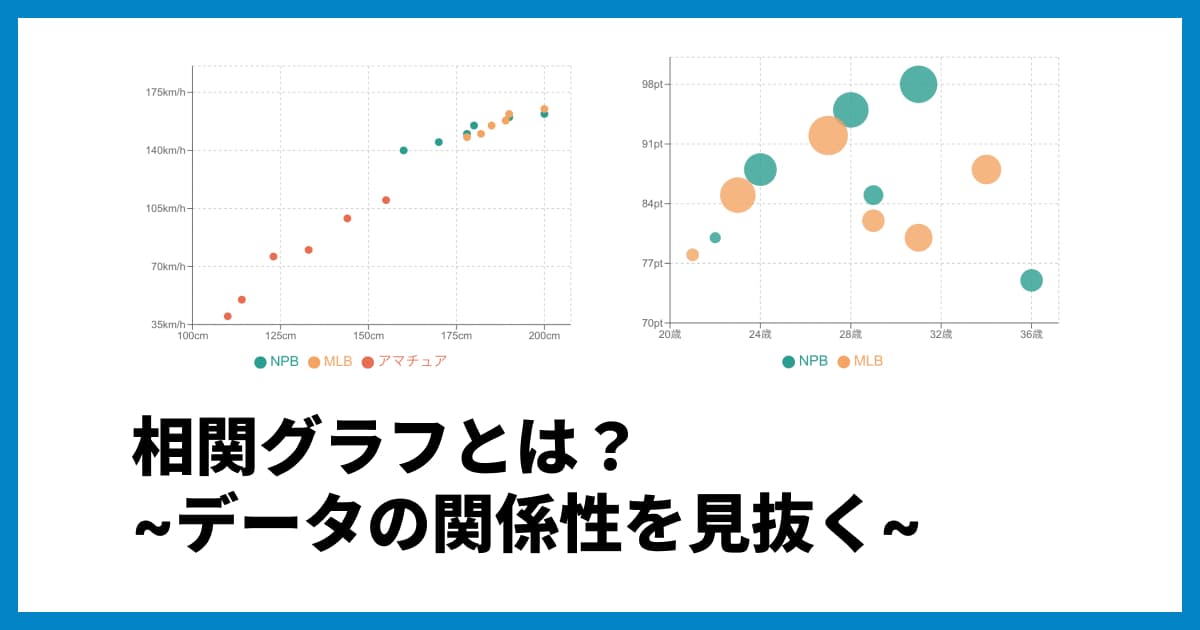
  片方が増える（減る）と、もう片方も増える（減る）関係です。点が右上がりの傾向で分布します。
  （例：勉強時間とテストの点数、身長と体重）

• 負の相関
  片方が増える（減る）と、もう片方は減る（増える）という逆の関係です。点が右下がりの傾向で分布します。
  （例：山の標高と気温、商品の価格と販売数）

• 無相関
  2つのデータに明確な関係性が見られない状態です。点は全体にまんべんなく散らばります。
  （例：視力と貯金額、今日の気分と株価）

このように、データの関係性を視覚的に捉えることで、数字の羅列だけでは分からないインサイトを得ることができます。

相関関係を可視化する代表格「散布図」

相関関係を調べる際に最もよく使われるグラフが散布図です。

散布図は、2つのデータをX軸（横軸）とY軸（縦軸）に対応させ、点がどこにプロットされるかを見ることで、一目で全体の傾向を把握できる非常に優れたグラフです。

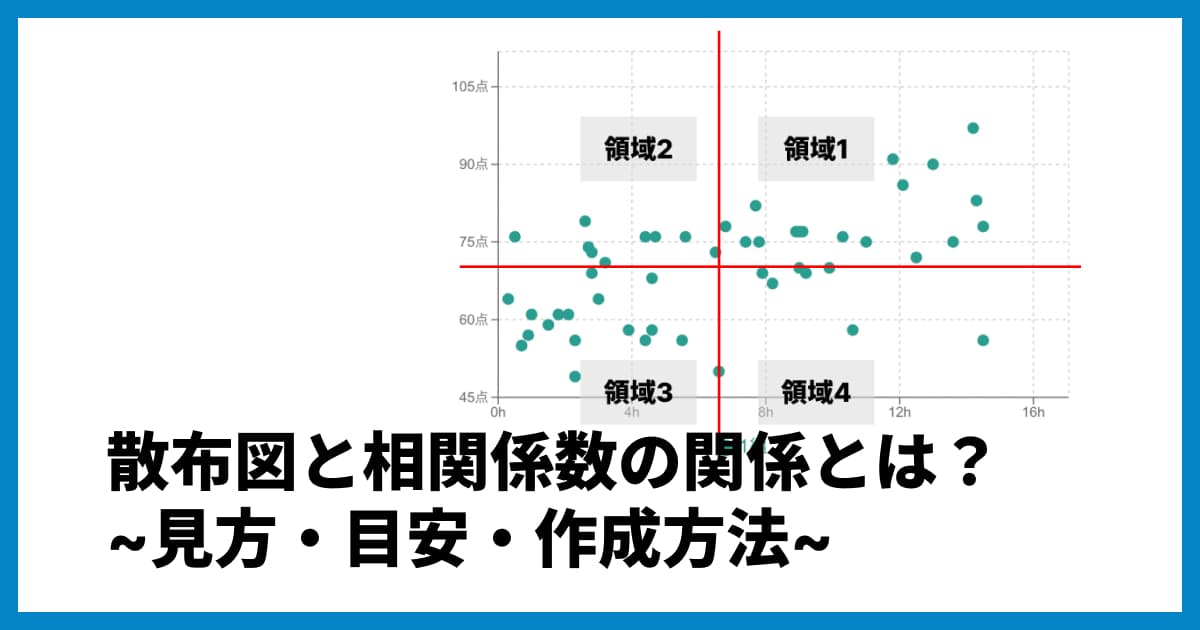
散布図の見方のポイントは、点の集まりが「どのような形に分布しているか」です。

• 右肩上がりに分布していれば「正の相関」
  

  

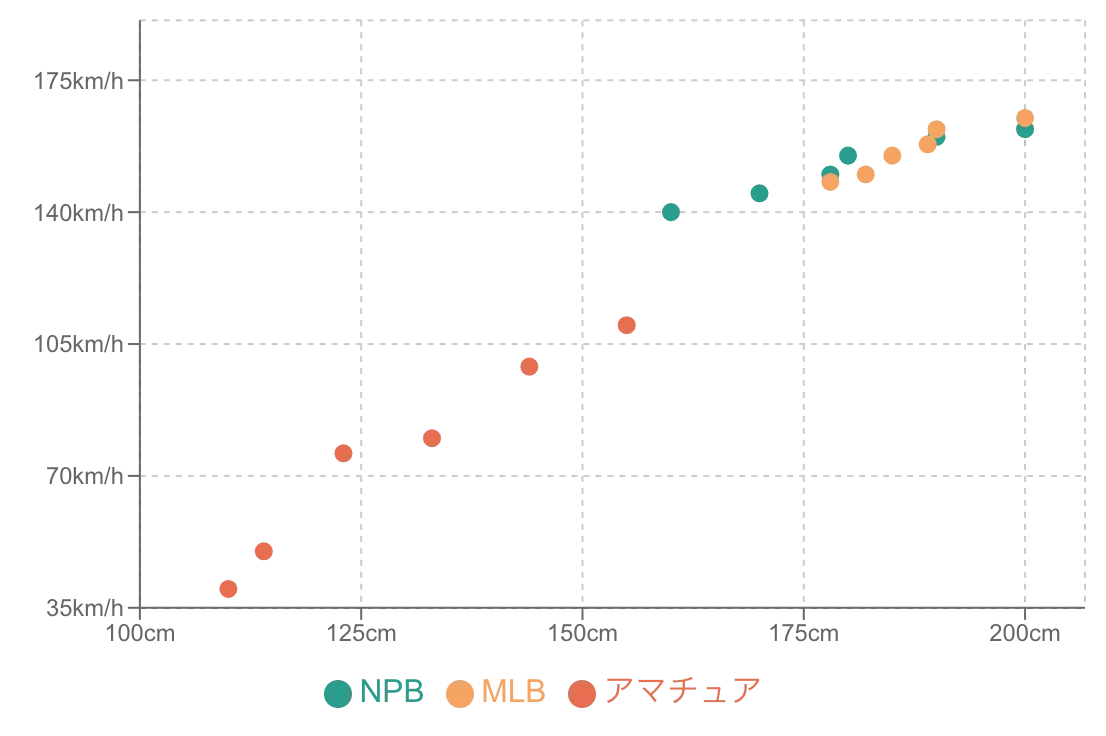
• 右肩下がりに分布していれば「負の相関」
  

  

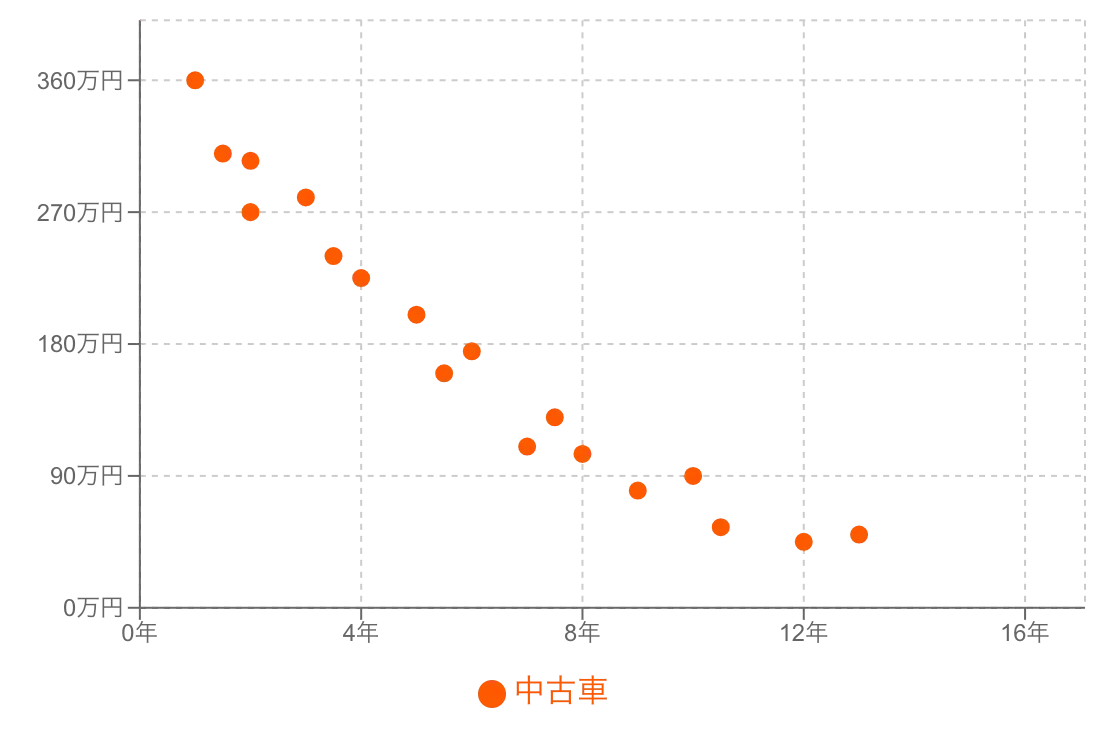
• 全体に散らばっていれば「無相関」
  

  

また、点の集まりが直線に近いほど「相関が強い」と判断でき、バラバラに広がっているほど「相関が弱い」と読み取ることができます。

【実践】オンラインツールで相関グラフ（散布図）を3ステップで作成！

「相関グラフが便利なのは分かったけど、作るのは難しそう…」と感じるかもしれません。Excelなどでも作成は可能ですが、もっと手軽に、そして見栄えの良いグラフを作りたい方には、当サイトが運営するオンライングラフ作成ツール xGrapher がおすすめです。

xGrapher は、会員登録不要・インストール不要で、ブラウザ上ですぐにグラフ作成を始められます。ここでは、xGrapherを使って散布図を作成する簡単な3つのステップをご紹介します。

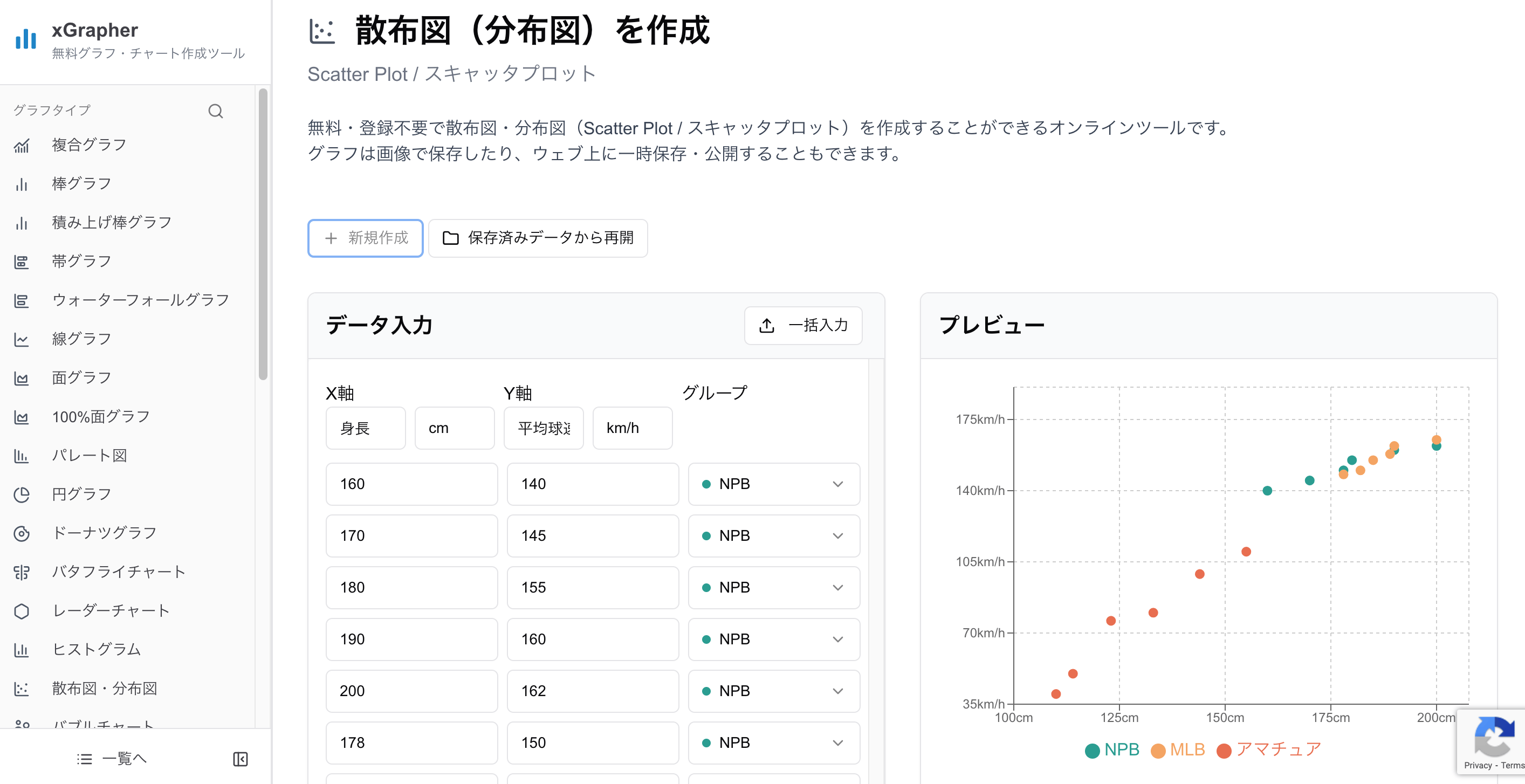
Step 1: データの準備
まず、グラフにしたい2つのデータを用意します。お手持ちのCSVファイルをアップロードするか、スプレッドシートなどからデータを直接コピー＆ペーストするだけで準備は完了です。

Step 2: グラフの種類で「散布図」を選択
グラフの種類一覧から「散布図」を選びます。xGrapherでは、散布図以外にも様々な種類のグラフを直感的に選ぶことができます。

Step 3: 軸の設定とデザイン調整
X軸とY軸にどのデータを割り当てるかを選択します。あとは、グラフのタイトルや色、点の大きさなどを自由にカスタマイズすれば、あっという間に美しい相関グラフの完成です。

このように、専門的な知識がなくても、誰でも簡単にデータに基づいた説得力のあるグラフを作成できます。ぜひ一度、xGrapher を試してみてください。

散布図と合わせて理解したい「相関係数」とは？

散布図でデータの関係性を視覚的に捉えたら、次はその関係性の「強さ」と「向き」を客観的な数値で表してみましょう。そのために使われるのが相関係数（r）です。

相関係数の値はどう読み取れば良いのか？

相関係数は、-1から+1までの範囲の値を取り、2つのデータの関係性を以下のように示します。

• +1に近いほど：強い正の相関があることを意味します。散布図では、点が右上がりの直線に非常に近い形で分布します。

• -1に近いほど：強い負の相関があることを意味します。散布図では、点が右下がりの直線に非常に近い形で分布します。

• 0に近いほど：相関がほとんどない（無相関）ことを意味します。散布図では、点に明確な傾向が見られず、ランダムに散らばります。

一般的に、相関係数の絶対値（プラスマイナスを無視した数値）を使って、以下のように相関の強さを判断します。

このように、散布図の「見た目の印象」と相関係数という「客観的な数値」を組み合わせることで、より深く、そして正確にデータ間の関係性を読み解くことができるのです。

相関係数はどうやって計算するの？（考え方の紹介）

「相関係数が便利なのは分かったけど、一体どうやって計算しているの？」と疑問に思う方もいるかもしれません。

現在ではExcelや専門のツールが自動で計算してくれますが、その基本的な考え方を知っておくと、より深く相関を理解できます。計算は、大きく分けて以下の3ステップで行われます。

Step 1: 各データの「中心（平均）」からの「ズレ（偏差）」を求める

まず、それぞれのデータセット（例：勉強時間、テストの点数）の平均値を出します。次に、個々のデータがその平均からどれだけ離れているか（＝偏差）を計算します。平均より大きければプラス、小さければマイナスになります。

Step 2: 2つのデータの「ズレ」を掛け合わせ、その平均を出す（共分散）

次に、ペアとなるデータ（Aさんの勉強時間の偏差と、Aさんのテストの点数の偏差）を掛け合わせます。この計算をすべてのデータで行い、その平均値を出します。これを共分散と呼びます。

• 勉強時間もテストの点数も平均より上（プラス × プラス）なら、積はプラスになります。

• 勉強時間もテストの点数も平均より下（マイナス × マイナス）でも、積はプラスになります。

• 片方が平均より上で、もう片方が下（プラス × マイナス）だと、積はマイナスになります。

この積の平均（共分散）が大きなプラスなら「正の相関」の傾向、大きなマイナスなら「負の相関」の傾向があると言えます。

Step 3: それぞれのデータの「ばらつき具合」で割って調整する（正規化）

最後に、Step2で計算した共分散を、それぞれのデータが持つ「ばらつきの大きさ（標準偏差）」で割り算をします。

これは、データの単位（例：「時間」と「点」）が異なると共分散の値が大きく変わってしまうのを補正し、-1から+1の間に数値を収めるための「正規化」というプロセスです。この最終的な結果が「相関係数」となります。

このように、相関係数は「2つのデータが、それぞれの平均から同じような方向に、どのくらいの強さでズレているか」を示す指標なのです。

相関グラフを読み解く上での最重要ポイント：「相関」と「因果」の違い

相関グラフを扱う上で、絶対に注意しなければならないのが「相関関係」と「因果関係」を混同しないことです。

• 相関関係: 2つの事柄が「連動して変化」している状態。

• 因果関係: 片方が「原因」で、もう片方が「結果」である状態。

例えば、「アイスクリームの売上」と「水難事故の発生件数」のデータを見ると、おそらく強い正の相関が見られるでしょう。しかし、これは「アイスが売れると水難事故が起きる」という因果関係を意味するわけではありませんよね。

この場合、「気温の上昇」という第3の因子が、アイスの売上（原因）と水難事故（原因）の両方に影響を与えています。このように、見かけ上の相関（擬似相関）に騙されず、「なぜこのような関係が生まれるのか？」と一歩踏み込んで考えることが、正しいデータ分析の鍵となります。

相関だけじゃない！データ可視化の様々な手法

今回は相関関係を見るための散布図を中心に解説しましたが、データの特性や伝えたいメッセージによって、最適なグラフの形は異なります。

例えば、カテゴリーごとの量を比較したいなら棒グラフ、時間の経過による変化を示したいなら折れ線グラフ、全体に対する割合を示したいなら円グラフが適しています。

xGrapherでは、これらの基本的なグラフも全て簡単に作成可能です。どのようなグラフを使えば良いか迷った際は、ぜひ当サイトの他のコラムも参考にしてみてください。データ可視化のヒントがたくさん見つかるはずです。

→ データ分析に役立つ記事一覧はこちら

相関グラフに関するQ&A

Q1. 相関係数とは何ですか？

A1. 相関関係の強さや向きを-1から+1までの数値で表した指標です。+1に近いほど強い正の相関、-1に近いほど強い負の相関、0に近いほど相関がない（または弱い）ことを意味します。散布図と合わせて見ることで、より客観的に関係性を評価できます。

Q2. 相関が「強い」「弱い」の基準はありますか？

A2. 分野によって解釈は異なりますが、一般的に相関係数の絶対値が0.7以上なら「強い相関」、0.4〜0.7なら「中程度の相関」、0.2〜0.4なら「弱い相関」、0.2未満なら「ほとんど相関なし」と判断されることが多いです。

Q3. 散布図以外のグラフで相関を見ることはできますか？

A3. はい、できます。例えば、複数の変数間の相関の強さを色の濃淡で一覧表示する「ヒートマップ」や、複数の散布図を一覧表示する「散布図行列」などがあります。これらは、3つ以上の変数間の関係性を探る際に特に有効です。

Q4. グラフに「外れ値」（他の値から大きく外れた値）がある場合はどうすればいいですか？

A4. 外れ値は、相関関係の解釈に大きな影響を与える可能性があります。まずは入力ミスなどではないかを確認し、もしそれが特異なデータである場合は、分析から除外するか、外れ値を含めた場合と除外した場合の両方で分析し、結果を比較検討することが重要です。

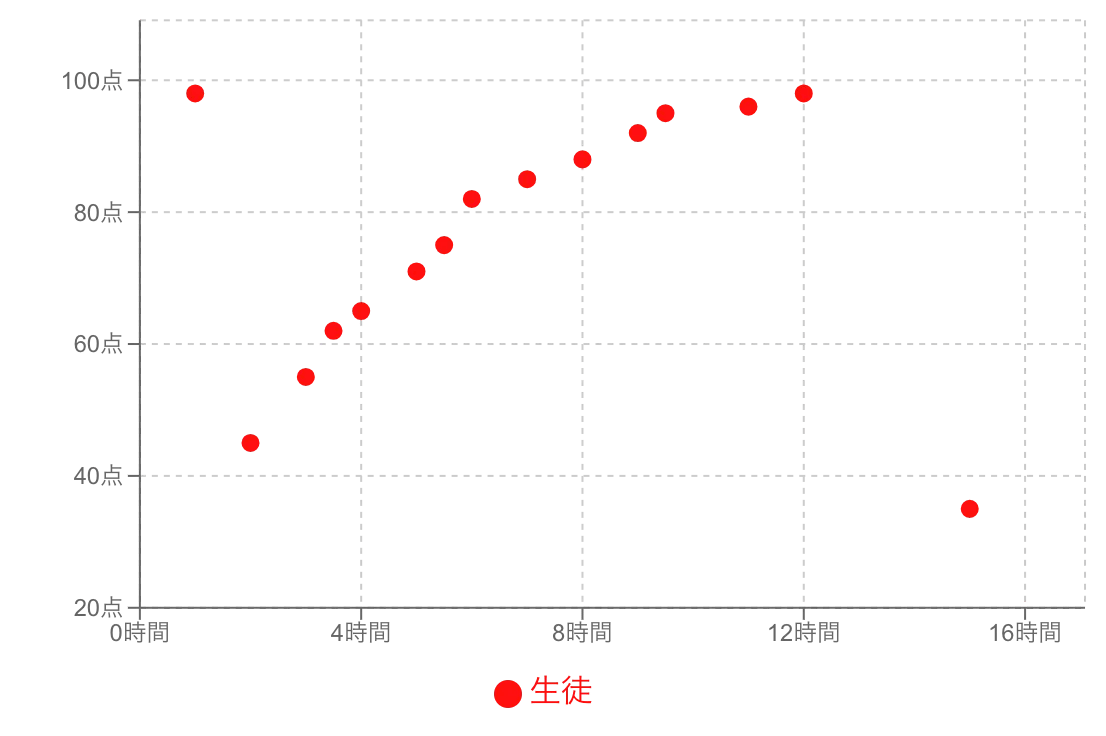
Q5. 3つ以上のデータの関係性を見たい場合はどうすればいいですか？

A5. 2次元の散布図に、点の色や大きさで3つ目の変数を表現する「バブルチャート」という手法があります。また、Q3で触れた「散布図行列」や「ヒートマップ」も、多変数の関係性を概観するのに役立ちます。
>> 3つ目の変数を表現するバブルチャートとは？

まとめ

今回は、データ間の隠れた関係性を見つけ出す「相関グラフ」について、基本となる考え方から代表的な散布図の見方、そしてオンラインツールを使った簡単な作成方法までをご紹介しました。

• 相関には「正の相関」「負の相関」「無相関」の3パターンがある。

• 相関を視覚化するには散布図が最適。

• 相関関係は因果関係と同じではない点に注意が必要。

• xGrapher を使えば、誰でも簡単に美しいグラフが作成できる。

データ分析は、もはや専門家だけのものではありません。xGrapherのようなツールを活用して、ぜひあなたのビジネスや研究、学習にデータ可視化を取り入れてみてください。きっと新しい発見があるはずです。