箱ひげ図を作成
Box Plot
無料・登録不要で箱ひげ図を作成することができるオンラインツールです。
グラフは画像で保存したり、ウェブ上に一時保存・URLで公開することもできます。
箱ひげ図は、データの分布を視覚的に表現するためのグラフで、中央値、四分位数、外れ値を示すのが特徴です。
これにより、データのばらつきや中心傾向を理解しやすくなります。
データ入力
各行に「ラベル」とカンマ/スペース区切りの数値を入力してください（例: 100, 200 250 450, 650）
設定・スタイル
プレビュー
箱ひげ図はどんなグラフですか？
データの分布を「中央値」「四分位数（Q1・Q3）」「外れ値」で要約して示すグラフです。 ばらつきや中心の位置、歪み、外れ値の有無を一目で把握できます。
箱・ひげ・外れ値は何を表していますか？
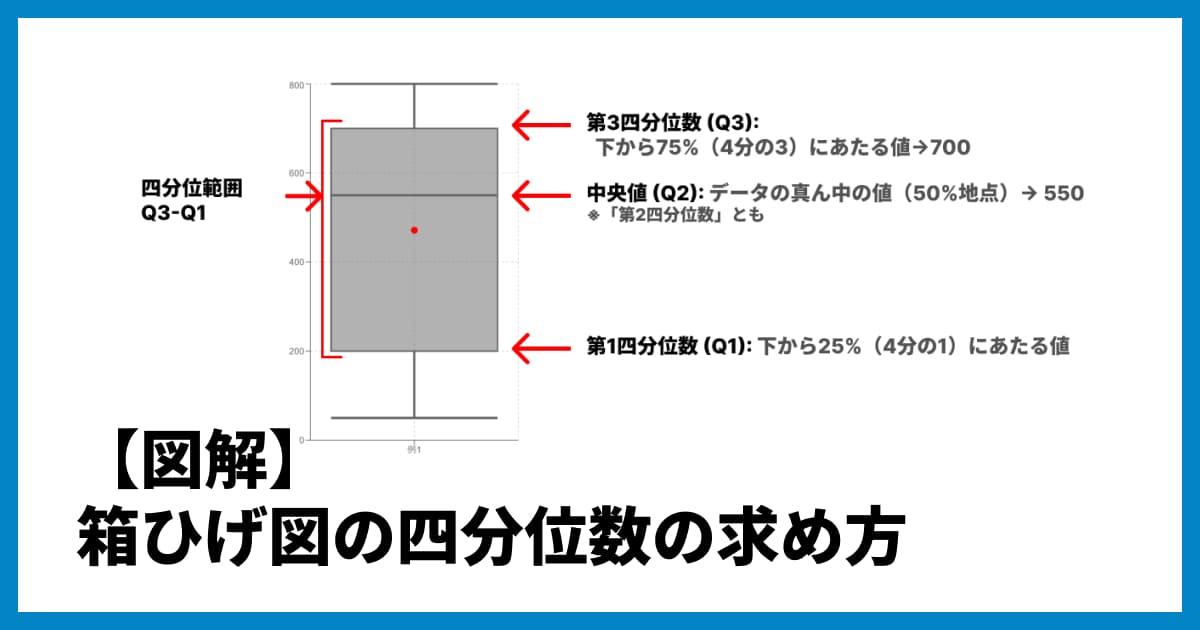
- 箱（Box）：第1四分位数 Q1 から第3四分位数 Q3（中央50%の範囲）
- 箱の中央線：中央値（50パーセンタイル）
- ひげ（Whisker）：通常は Q1−1.5×IQR と Q3＋1.5×IQR の範囲内で最も内側の観測値まで
- IQR：四分位範囲（Q3 − Q1）
- 外れ値：ひげの外側に位置する観測値（点で表示）
どんなデータ・場面に向いていますか？
- 群（カテゴリ）間の分布比較（例：クラス別テスト点、製品ロット別測定値）
- 外れ値の検出や分散の違いの把握
- 平均だけでは分からない分布の広がり・偏りの確認
データはどのように準備・入力すればよいですか？
- カテゴリ（グループ）ごとに複数の数値データを用意します。
- 数値のみを使用してください（空欄や非数値は無視・除外されます）。
- 小数も扱えます。単位がある場合は同一単位にそろえてください。
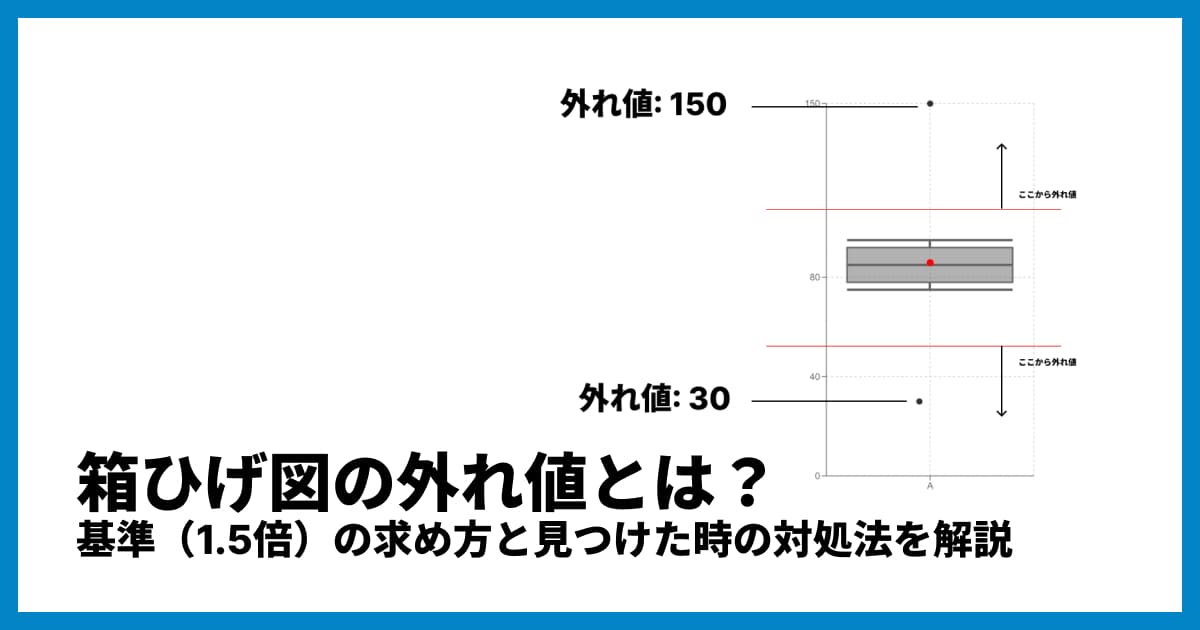
外れ値はどのように扱われますか？
通常、Q1−1.5×IQR より小さい値、または Q3＋1.5×IQR より大きい値が外れ値として点で表示されます。 外れ値は計算から除外されるわけではなく、分布の可視化上で強調されます。
五数要約とは何ですか？
- 最小値（しばしば下ひげの端に対応）
- 第1四分位数 Q1
- 中央値（第2四分位数）
- 第3四分位数 Q3
- 最大値（しばしば上ひげの端に対応）
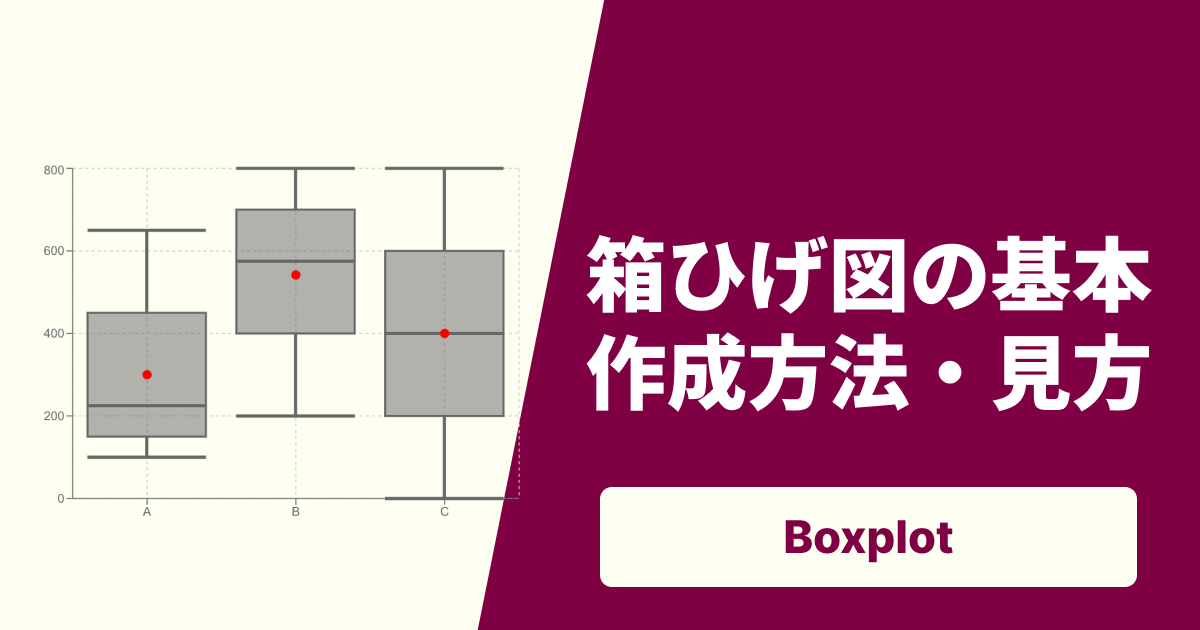
複数グループの比較はできますか？
複数のカテゴリ（グループ）を並べて表示することで、分布の中心・ばらつき・外れ値を比較できます。
サンプル数が少ない場合の注意点は？
- 中央値や四分位数の推定が不安定になりやすい
- 外れ値の判定が過敏になる可能性がある
- 十分なサンプル数を確保するか、他の可視化（散布図・ストリッププロット等）も併用すると安心です
箱ひげ図の利点と限界は？
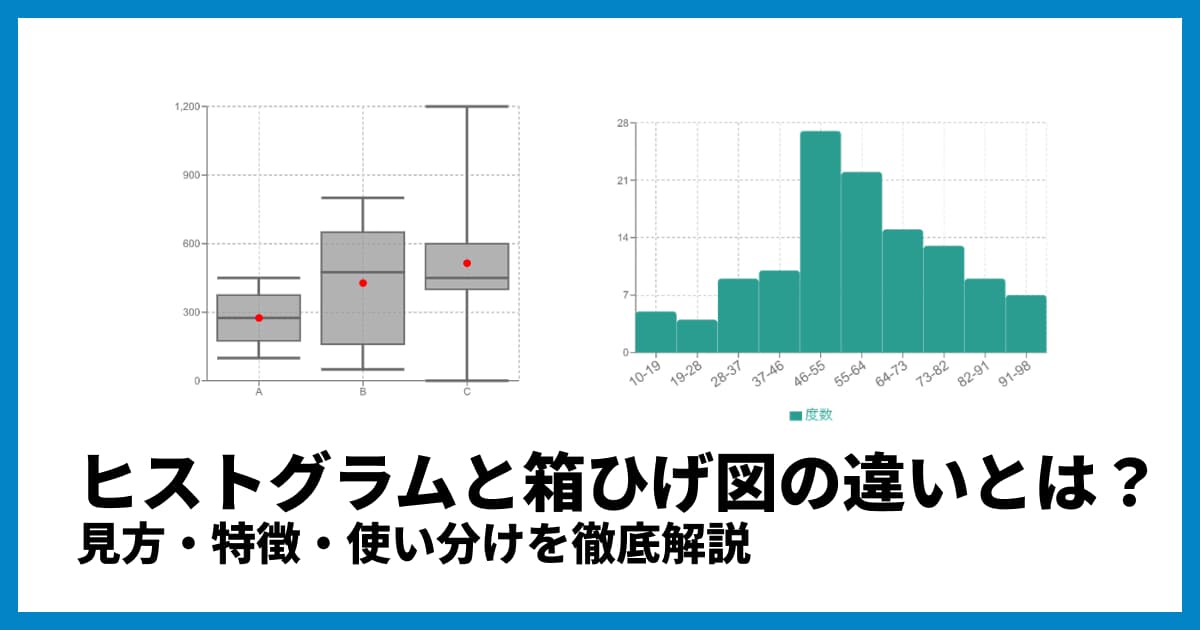
箱ひげ図から読み取れること／読み取れないことは？
- 読み取れる：中央値、ばらつき（IQR）、歪み、外れ値の有無
- 読み取りにくい：分布の細かな形（多峰性、正確な密度の形状）
画像として保存するにはどうすればよいですか？
プレビューエリアの下にある「画像をダウンロード」ボタンをクリックすると、作成したグラフをPNG/JPEG/SVG形式・画質を指定してダウンロードできます。
アスペクト比を変更したい場合は、プレビューの枠線の右下にあるハンドルをドラッグして調整できます。
アスペクト比を変更したい場合は、プレビューの枠線の右下にあるハンドルをドラッグして調整できます。
データを一時保存するには？
プレビューエリアの下にある「グラフを保存・公開」ボタンをクリックすると、作成したグラフを一時的に保存できます。
保存した際に発行されるURLとPWで後で再編集することが可能です。グラフをURLで一般公開することもできます。
保存した際に発行されるURLとPWで後で再編集することが可能です。グラフをURLで一般公開することもできます。
保存したデータを読み込むには？
「保存済みデータから再開」ボタンからグラフを読み込むことができます。 読み込む際には、保存した際に発行されたURLとPWを入力してください。
CSVやコピー＆ペーストで一括入力できますか？
「一括入力」ボタンからダイアログを開き、スプレッドシート/ExcelやHTML表をコピーして貼り付けるか、CSVファイルを選択してください。
各行・各列への入力内容は画面をご確認ください。
貼り付け後プレビューで編集し「確定して反映」でグラフ・チャートへ反映されます。
各行・各列への入力内容は画面をご確認ください。
貼り付け後プレビューで編集し「確定して反映」でグラフ・チャートへ反映されます。
&w=3840&q=75)
&w=3840&q=75)
&w=3840&q=75)