擬似相関（見せかけの相関・偽相関）とは？データに騙されないための具体例と見抜き方

2025年10月24日2025年10月27日

「データを見ると、Aが増えるとBも増えている。だからAはBの原因だ！」
ビジネスや日常生活で、このように結論づけたくなる場面はありませんか？しかし、その関係性、もしかしたら「擬似相関（偽相関・見せかけの相関）」かもしれません。

偽相関（英: Spurious correlation）は「見せかけの相関」や「疑似相関」とも呼ばれます。これは、2つの事柄（変数）の間に、あたかも関係があるかのように見える（相関関係がある）のに、実際には直接的な因果関係がない状態を指します。

データ分析が身近になった今、この偽相関に気づかないと、間違った判断をしてしまう可能性があります。この記事では、偽相関とは何か、なぜ起こるのか、そしてデータに騙されないための見抜き方を、具体例とともにわかりやすく解説します。

なぜ起こる？擬似相関（偽相関・見せかけの相関）のよくある具体例

擬似相関は、多くの場合、2つの事柄に共通して影響を与える「第3の変数（交絡因子）」が隠れているために発生します。言葉だけでは分かりにくいので、有名な具体例を見てみましょう。

例1：アイスクリームの売上と水難事故の件数

最もよく知られた例です。データを見ると、「アイスクリームの売上が増える時期」と「水難事故の件数が増える時期」は、確かに連動している（正の相関がある）ように見えます。

しかし、「アイスクリームを食べると水難事故に遭いやすくなる」あるいは「水難事故が増えるとアイスクリームが売れる」という直接的な因果関係はあるでしょうか？

答えは「いいえ」です。もうお気づきかもしれませんが、ここには「気温」という第3の変数が隠れています。

気温が上がる → アイスクリームが売れる
気温が上がる → 海や川で泳ぐ人が増え、水難事故が増える

つまり、「アイスクリームの売上」と「水難事故の件数」は、どちらも「気温の上昇」という共通の原因によって引き起こされた結果であり、この2つに直接の因果関係はないのです。

例2：小学生の「握力」と「計算力」

ある小学校でデータを取ったところ、「握力が強い生徒」ほど「計算力が高い」という相関が見られました。では、握力を鍛えれば計算力が上がるのでしょうか？

[一見相関がありそうな握力と計算力の散布図]

これも偽相関の可能性が高いです。隠れた第3の変数は「年齢（学年）」です。

年齢が上がる（高学年になる） → 体が成長し、握力が強くなる
年齢が上がる（高学年になる） → 学習が進み、計算力が上がる

1年生と6年生を比べれば、当然どちらの数値も高くなる傾向があります。これも「年齢」という交絡因子による見せかけの相関です。

[学年で色分けした握力と計算力の散布図]

例3：コンビニの店舗数と犯罪の発生件数

地域ごとのデータを見ると、「コンビニの店舗数が多い地域」ほど「犯罪の発生件数が多い」という相関が見られることがあります。これは「コンビニが犯罪を誘発している」ということでしょうか？

[一見相関がありそうなコンビニの店舗数と犯罪の発生件数の散布図]

これも短絡的です。おそらく、「人口（または都市化の度合い）」が影響しています。

人口が多い（都市部である） → コンビニの需要が高く、店舗数が多くなる
人口が多い（都市部である） → 様々な人が集まるため、犯罪の発生件数も多くなる

[人口規模で色分けしたコンビニの店舗数と犯罪の発生件数の散布図]

このように、一見関係がありそうなデータも、一歩引いて「他に共通の原因はないか？」と考えるクセをつけることが重要です。

相関関係と因果関係は違う！データ分析で注意すべき理由

偽相関で起こる最大の問題は、「相関関係」と「因果関係」を混同してしまうことです。

相関関係: 2つの事柄が連動して変化する関係。（一方が増えるともう一方も増える/減る）
因果関係: 一方の事柄が原因となり、もう一方の事柄が結果として起こる関係。

偽相関は、「相関関係はあるが、因果関係はない」状態です。

もし、アイスクリームの例で「アイスが売れると事故が増える」と因果関係を誤解したら、「水難事故を減らすために、アイスの販売を禁止しよう」という、まったく見当違いな対策をとってしまうかもしれません。

ビジネスにおいても、「広告費を増やしたら売上が上がった」というデータ（相関関係）を見て、「広告費が売上の原因だ（因果関係）」と即断するのは危険です。もしかしたら、同時期に季節的な需要が高まった（第3の変数）だけかもしれません。

>> 相関関係と因果関係の違いとは？データ分析で間違う前に知りたい基本

データに基づいて正しい判断を下すためには、「これは本当に原因と結果の関係か？」「見せかけの相関ではないか？」と常に疑う視点が不可欠です。

※相関関係についてより詳しく知りたい方は、相関係数の計算方法を解説した「相関係数(r)とは？計算方法やエクセルでの求め方を解説」や「相関とは？相関関係と因果関係の違い、相関係数の求め方まで解説」も参考にしてみてください。

擬似相関（偽相関・見せかけの相関）を見抜く3つのステップ

では、データを見たときに、擬似相関に騙されないようにするにはどうすればよいでしょうか。以下の3つのステップで考えてみましょう。

ステップ1：本当に因果関係があるか「常識」で疑う

まず、データが示す関係性が、常識的に考えて「原因と結果」として成り立つか自問します。「握力を鍛えたら計算が速くなるか？」「アイスを食べたら溺れやすくなるか？」と考えると、直感的に「おかしい」と感じられるはずです。

この「直感」や「その分野の知識（ドメイン知識）」が、偽相関を見抜く第一歩となります。

ステップ2：隠れた「第3の変数」を探す

次に、「2つの事柄に共通して影響を与えそうな、別の要因はないか？」と考えます。これが「交絡因子」を探す作業です。

アイスと水難事故 → 「季節」や「気温」は関係ないか？
握力と計算力 → 「年齢」や「学年」は関係ないか？
コンビニと犯罪 → 「人口」や「駅からの距離」は関係ないか？

このように、背景にある要因を洗い出すことで、見せかけの関係性が見えてきます。

ステップ3：データを「可視化」して確認する

もし手元にデータがあるなら、グラフにして「可視化」することが非常に有効です。特に「散布図」は、2つの変数の関係性を見るのに最適です。

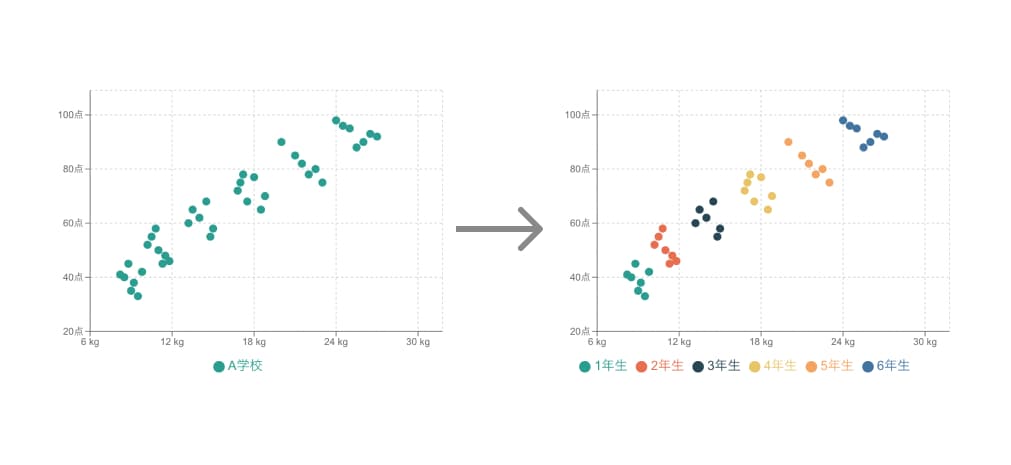
例えば、「握力」を横軸、「計算力」を縦軸にして散布図を描いたとします。もしこれが偽相関なら、データを「学年」で色分けしてみると、学年ごとのグループはバラバラなのに、全体として右上がりに見えているだけ、といった状況が視覚的にわかることがあります。

※散布図の基本的な見方については「散布図の見方とは？相関関係がひと目でわかるグラフを解説」で詳しく解説しています。

データは「散布図」で可視化して考えよう

擬似相関を疑うとき、相関係数（r）という数値だけを見ていると、数字の強さ（例： $r=0.8$ ）に引っ張られてしまいがちです。

※相関係数と散布図の関係については「散布図と相関係数の関係とは？読み取り方を解説」もご覧ください。

そんな時こそ、オンライングラフ作成ツールの xGrapher が役立ちます。xGrapherの散布図作成ツールを使えば、ExcelやGoogleスプレッドシートがなくても、Webブラウザ上でデータをコピペするだけで、誰でも簡単に散布図を作成できます。

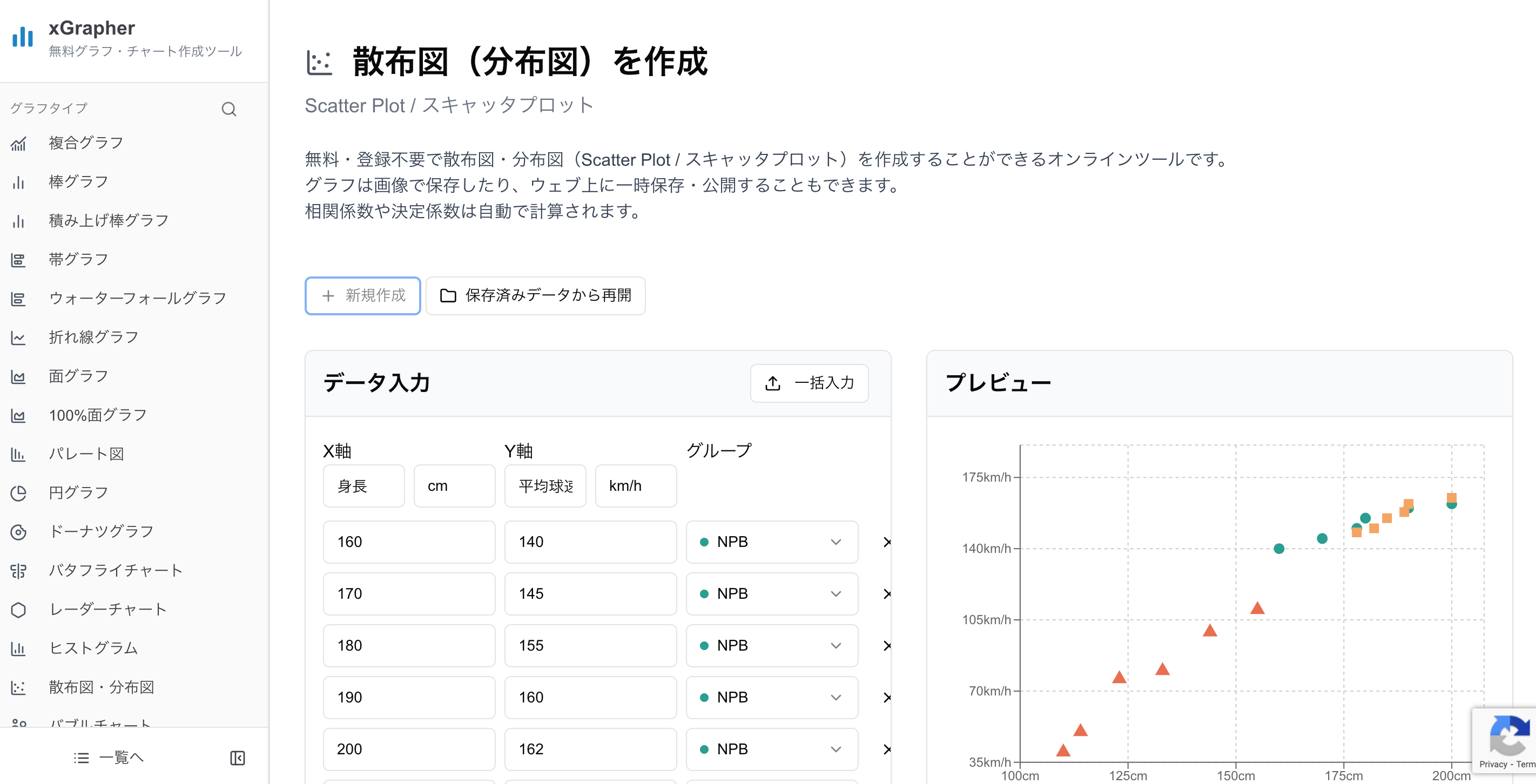
「このデータ、怪しいな」と思ったら、まずは散布図で可視化してみましょう。さらに、第3の変数（例：年齢、気温、地域など）でデータをグループ分け（色分け）してプロットしてみることで、偽相関の構造がより明確に見えてくることがあります。

※Excelやスプレッドシートでの散布図の作り方は「Excel(エクセル)で散布図を作成する方法」や「Googleスプレッドシートで散布図を作成する方法」でも解説しています。

まとめ

今回は、データ分析で陥りがちな「擬似相関（偽相関・見せかけの相関）」について解説しました。

擬似相関とは、2つの事柄に相関関係が見えるが、直接の因果関係はない状態。
多くの場合、第3の変数（交絡因子）が両方に影響している（例：アイスと水難事故の原因は「気温」）。
「相関関係は、必ずしも因果関係を意味しない」ことを常に意識する。
偽相関を見抜くには、「常識で疑う」「第3の変数を探す」「散布図などで可視化する」ことが重要。

データは強力な武器ですが、その表面的な関係性だけを見て判断を誤る危険性もはらんでいます。ぜひ「偽相関」の視点を持ち、データをより深く読み解くスキルを身につけてください。

偽相関に関するQ&A

Q1. 偽相関と疑似相関は同じ意味ですか？

A1. はい、同じ意味で使われることがほとんどです。「偽相関（ぎそうかん）」「疑似相関（ぎじそうかん）」「見せかけの相関」「見かけ上の相関」は、すべて本記事で解説した「相関はあるが因果関係はない」状態を指す言葉です。

Q2. 相関係数が高ければ、因果関係があると言えますか？

A2. いいえ、言えません。相関係数はあくまで「2つの変数がどれだけ直線的に連動しているか」を示す数値です。相関係数が+1や-1に近くても、それが偽相関である可能性は常にあります。因果関係の有無は、相関係数の値だけでは判断できません。
（※相関係数の基礎については「相関係数(r)とは？計算方法やエクセルでの求め方を解説」をご覧ください。）

Q3. 偽相関と「見せかけの回帰」は違いますか？

A3. 似ていますが、厳密には異なる文脈で使われます。「偽相関（疑似相関）」は主に統計学全般で使われる言葉です。一方、「見せかけの回帰（Spurious Regression）」は、特に「時系列データ」の分析において、お互いに無関係なトレンドを持つデータ同士を回帰分析すると、統計的に有意な関係があるように見えてしまう現象を指します。

Q4. 偽相関かどうかを統計的に調べる方法はありますか？

A4. あります。第3の変数（交絡因子）の影響を取り除いた上での相関関係を調べる「偏相関係数」を計算する方法などがあります。ただし、どの変数を第3の変数として疑うかは、その分野の専門知識（ドメイン知識）が必要になります。

Q5. 偽相関を避けるために、データ分析で最も重要なことは何ですか？

A5. 「相関関係 ≠ 因果関係」という原則を絶対に忘れないことです。そして、データや数値だけを鵜呑みにせず、そのデータが生まれた背景や文脈（どのような第3の変数が隠れている可能性はないか）を考える「批判的思考」を持つことが最も重要です。データを可視化することも、その助けになります。

Q6. 偽相関の例は他にもありますか？

「消防士の数と火災の被害額」

相関: 火災現場に出動した「消防士の数」が多いほど、「火災による被害額」も大きい。（正の相関）
隠れた変数（交絡因子）: 火災の規模
解説: これは、「消防士が多いから被害が拡大した」のではありません。「火災の規模」が大きいために、「被害額が大きく」なり、同時に「多くの消防士が必要になった」というだけです。原因と結果が逆に見えやすい例でもあります。

「子供の靴のサイズと読解力」

相関: 「靴のサイズ」が大きい子供ほど、「読解力（または語彙力）」が高い。（正の相関）
隠れた変数（交絡因子）: 年齢
解説: これは記事の「握力と計算力」の例と全く同じ構造です。「年齢」が上がるにつれて、当然ながら「体（足）が成長」し、同時に「学習が進んで読解力が上がる」ため、2つの変数に相関があるように見えます。

「コウノトリの生息数と出生率」

相関: （ヨーロッパの特定の地域で）「コウノトリの生息数」が多い地域ほど、「人間の出生率」も高い。（正の相関）
隠れた変数（交絡因子）: 都市化の度合い（または地域の面積）
解説: これは「コウノトリが赤ちゃんを運んでくる」という伝承を裏付けるかのようなデータですが、実際は違います。「田舎（非都市部）」は、「都市部」に比べてコウノトリが巣を作りやすい（煙突のある家が多いなど）環境であり、同時に、歴史的に出生率も高い傾向がありました。

「コーヒーの消費量と肺がんの発生率」

相関: 過去の調査で、「コーヒーの消費量」が多い人ほど、「肺がんの発生率」が高いというデータが見られました。（正の相関）
隠れた変数（交絡因子）: 喫煙
解説: これは、「コーヒーが肺がんの原因だ」ということを意味しません。調査対象の集団において、「コーヒーをよく飲む人」には「タバコをよく吸う人」が（偶然または生活習慣として）多かったのです。肺がんの真の（主要な）原因は「喫煙」であり、喫煙がコーヒーの消費と肺がんの両方に関係していたため、見せかけの相関が生まれました。

「メイン州の離婚率とマーガリンの消費量」

相関: （米国の特定の期間で）「メイン州の離婚率」と「一人当たりのマーガリン消費量」が、非常に高い相関（ $r=0.99$ ）を示した。（正の相関）
隠れた変数（交絡因子）: （おそらく）存在しない。単なる偶然の一致。
解説: これは、データサイエンティストのTyler Vigen氏が発見した有名な「無関係な相関」の例です。2つの事柄に論理的なつながりも、隠れた第3の変数も（おそらく）ありません。世の中には膨大な数のデータが存在するため、全く無関係なもの同士が「偶然」高い相関を示すことがあります。これも偽相関の一種であり、「相関関係は因果関係を意味しない」という強力な実例です。