相関係数の計算方法を解説!公式とExcelでの簡単な求め方を紹介

「データ分析のために、2つのデータの関係性を数値で知りたい」
「相関係数という言葉は聞くけど、どうやって計算するんだろう?」
「Excelで簡単に計算できる方法はないかな?」
そんな風に思っていませんか? 相関係数は、2つの変数の間にどれくらい「関係」があるかを示す、-1から1までの値をとる統計指標です。
一般的に「相関係数」と言うと「ピアソンの積率相関係数」を指すことが多く、これは身長と体重のような「量的データ」間の直線的な関係を測るのに使われます。
しかし、データが「満足度の5段階評価」や「成績の順位」のような「順序データ」である場合、ピアソンの相関係数ではうまく関係性を測れないことがあります。その場合は「スピアマンの順位相関係数」や「ケンドールの順位相関係数」といった別の指標が使われます。
この記事では、まず最も基本的なピアソンの相関係数の意味と計算方法を詳しく解説し、その後でスピアマンとケンドールの計算方法についても触れていきます。
この記事の内容(目次)
そもそも相関係数とは?(ピアソンの積率相関係数)
最も一般的に使われるピアソンの積率相関係数(記号 で表されることが多い)は、2種類のデータ(変数)間の直線的な関係の強さと向きを示す指標です。
値は-1から+1の間をとります。
+1に近いほど「強い正の相関」(一方が増えるともう一方も増える傾向が強い)
-1に近いほど「強い負の相関」(一方が増えるともう一方が減る傾向が強い)
0に近いほど「相関が弱い」(2つのデータ間の直線的な関係はほとんどない)
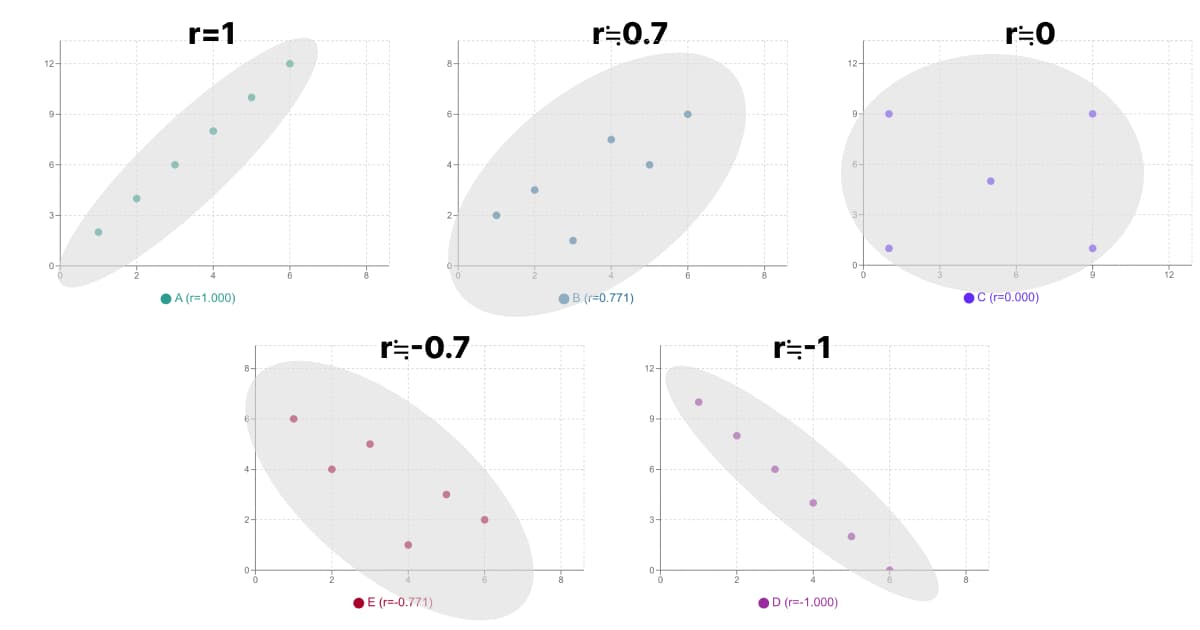
例えば、「身長と体重」には正の相関が、「勉強時間とゲームの時間」には負の相関が見られるかもしれません。
相関係数の詳しい意味や散布図との関係については、こちらの記事も参考にしてみてください。
相関係数を計算する2つの主な方法
ピアソンの相関係数を計算するには、大きく分けて2つの方法があります。
公式を使って手計算(または電卓)で求める方法
計算のプロセスを理解したい場合
共分散や標準偏差といった他の統計量も同時に求めたい場合
ExcelやGoogleスプレッドシートの関数を使う方法
手軽に、素早く相関係数だけを知りたい場合
まずは計算の仕組みを理解するために公式を使った方法から見ていき、その後で簡単なツールの使い方を紹介します。
【ステップ別】公式を使ったピアソンの相関係数 計算方法
ピアソンの相関係数 は、「2つのデータの共分散」を「それぞれのデータの標準偏差の積」で割ることで求められます。
または
...と言われても、いきなり難しいですよね。
大丈夫です。この計算は、以下のステップに分けて順番に行えば必ずできます。
ここでは、5人の生徒の「数学の点数()」と「理科の点数()」という架空のデータを使って、具体的に計算してみましょう。
生徒 | 数学() | 理科() |
|---|---|---|
Aさん | 70 | 80 |
Bさん | 50 | 60 |
Cさん | 90 | 90 |
Dさん | 60 | 50 |
Eさん | 80 | 70 |
STEP1: データの平均値を求める
まず、それぞれのデータの平均値( と )を計算します。
数学の平均 70点
理科の平均 70点
STEP2: 各データの偏差を求める
次に、各データが平均値からどれだけ離れているか(=偏差)を計算します。偏差は「データ - 平均値」で求めます。
数学の偏差 ()
理科の偏差 ()
生徒 | 数学() | 理科() | 数学の偏差() | 理科の偏差() |
|---|---|---|---|---|
Aさん | 70 | 80 | 70 - 70 = 0 | 80 - 70 = 10 |
Bさん | 50 | 60 | 50 - 70 = -20 | 60 - 70 = -10 |
Cさん | 90 | 90 | 90 - 70 = 20 | 90 - 70 = 20 |
Dさん | 60 | 50 | 60 - 70 = -10 | 50 - 70 = -20 |
Eさん | 80 | 70 | 80 - 70 = 10 | 70 - 70 = 0 |
合計 | 350 | 350 | 0 | 0 |
平均 | 70 | 70 | - | - |
(※偏差の合計は必ず0になります)
STEP3: 偏差の2乗和と標準偏差を求める
次に、相関係数の分母に必要な「標準偏差」を求めます。標準偏差は「分散」の平方根です。
偏差の2乗を計算する
偏差の2乗の平均を求めて「分散」を出す
分散の平方根(ルート)をとって「標準偏差」を出す
生徒 | 数学の偏差() | 理科の偏差() | 数学の偏差の2乗 | 理科の偏差の2乗 |
|---|---|---|---|---|
Aさん | 0 | 10 | ||
Bさん | -20 | -10 | ||
Cさん | 20 | 20 | ||
Dさん | -10 | -20 | ||
Eさん | 10 | 0 | ||
合計 | 0 | 0 | 1000 | 1000 |
数学の分散
数学の標準偏差 14.14
理科の分散
理科の標準偏差 14.14
STEP4: 偏差の積和と共分散を求める
次に、相関係数の分子に必要な「共分散」を求めます。
数学の偏差と理科の偏差を掛け合わせる(偏差の積)
偏差の積の平均を求めて「共分散」を出す
生徒 | 数学の偏差 | 理科の偏差 | 偏差の積(偏差 偏差) |
|---|---|---|---|
Aさん | 0 | 10 | |
Bさん | -20 | -10 | |
Cさん | 20 | 20 | |
Dさん | -10 | -20 | |
Eさん | 10 | 0 | |
合計 | 0 | 0 | 800 |
共分散 160
STEP5: 共分散と標準偏差から相関係数を計算する
ついに最後のステップです。STEP3とSTEP4で求めた値を使って、ピアソンの相関係数 を計算します。
相関係数
0.8
計算の結果、この5人の数学と理科の点数の相関係数は「0.8」となりました。これは「強い正の相関がある」ことを示しています。
[今回のデータを散布図]
実際の散布図を見ても右肩あがりの傾向が見て取れます。
.png)
(※補足:ここでは標本標準偏差・標本共分散を使いましたが、不偏分散などを使う場合もあります。ただし、相関係数を計算する上では、どちらで計算しても最終的な の値は同じになります。)
【簡単】Excelやスプレッドシートでのピアソンの相関係数 計算方法
手計算は大変でしたが、ExcelやGoogleスプレッドシートを使えば、ピアソンの相関係数は関数一つで一瞬で計算できます。
使う関数は CORREL関数 です。
=CORREL(配列1, 配列2)
配列1: 1つ目のデータ範囲(例:数学の点数リスト)配列2: 2つ目のデータ範囲(例:理科の点数リスト)
Excelでの手順
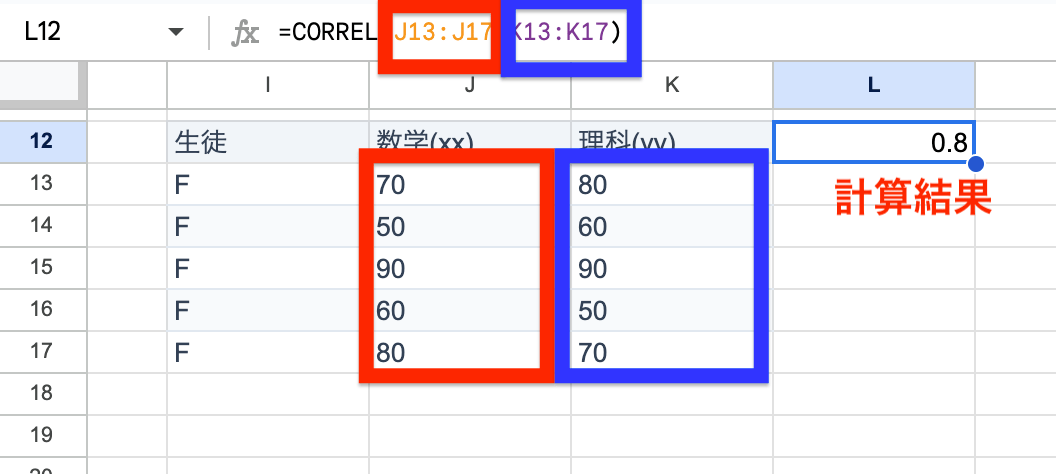
相関係数を表示したいセルを選択します。
=CORREL(と入力します。1つ目のデータ範囲(例では
B2:B6)をドラッグして選択し、カンマ,を入力します。2つ目のデータ範囲(例では
C2:C6)をドラッグして選択し、)で閉じます。Enterキーを押すと、相関係数(この例では
0.8)が表示されます。
Excelで散布図グラフも一緒に作成したい場合は、こちらの記事もご覧ください。
参考記事:Excel(エクセル)で散布図を作成する方法をわかりやすく解説
Googleスプレッドシートでの手順
手順はExcelと全く同じです。=CORREL(範囲1, 範囲2) を使うことで、簡単にピアソンの相関係数が計算できます。
スプレッドシートでの散布図作成については、こちらで詳しく解説しています。
参考記事:Googleスプレッドシートで散布図を作成する方法
【応用】順位データに使う相関係数の計算方法
ここまでは、点数や身長・体重のような「量的データ」を扱ってきました。
しかし、データが「満足度アンケート(5段階評価)」や「成績の順位」のような「順序尺度」の場合、ピアソンの相関係数(CORREL関数)は適切ではありません。
また、量的データであっても、極端な「外れ値」が少数ある場合、ピアソンの相関係数はその外れ値に大きく影響されてしまいます。
このような場合に使うのが、「順位相関係数」です。ここでは代表的な2つを紹介します。
1. スピアマンの順位相関係数 ()
スピアマンの順位相関係数は、データを数値そのものではなく、「順位(ランク)」に変換してから、ピアソンの相関係数と同じ計算を行うものです。
計算ステップ(概要):
データ を順位に変換します。(例:数学の点数が [70, 50, 90, 60, 80] → [3位, 5位, 1位, 4位, 2位])
データ を順位に変換します。(例:理科の点数が [80, 60, 90, 50, 70] → [2位, 4位, 1位, 5位, 3位])
変換した2つの順位データを使って、前述の「ピアソンの相関係数の計算方法(STEP1〜5)」をそのまま適用します。
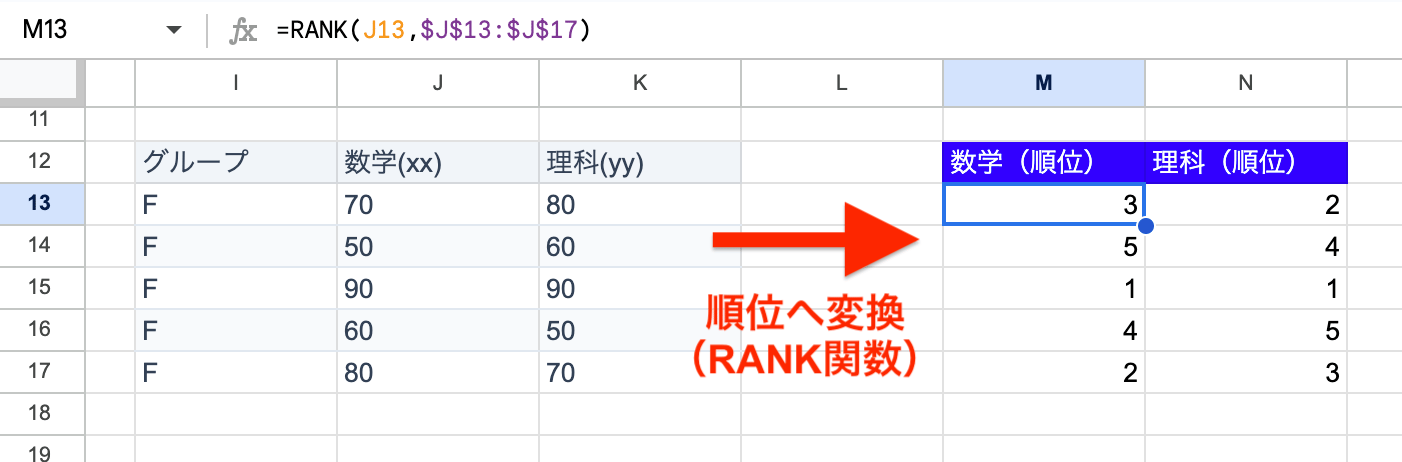
Excelには、スピアマンの相関係数を直接計算する関数は標準搭載されていません。RANK関数などでデータを順位に変換した後、その順位データに対してCORREL関数を使うことで計算できます。(計算結果は0.8)
スピアマンの相関係数は、外れ値の影響を受けにくく、データが直線関係でなくても「単調な関係(一方が増えれば、もう一方も増え続ける、または減り続ける)」であれば高い値を示す特徴があります。
>> スピアマンの順位相関係数とは?ピアソンとの違いなどわかりやすく解説
2. ケンドールの順位相関係数 ()
ケンドールの順位相関係数(ケンドールのタウ)は、スピアマンとは全く異なるアプローチで順位の相関を測ります。
計算ステップ(概要):
全データから2つのペアをランダムに選び出します。(例:(Aさん, Bさん), (Aさん, Cさん), (Bさん, Eさん)... など、全ての組み合わせ)
そのペアが「順序が一致している(AさんよりBさんの方が数学も理科も点数が高い)」か、「順序が逆転している(AさんよりBさんの方が数学は高いが、理科は低い)」かを数えます。
「一致したペアの数」と「逆転したペアの数」を使って、全体の傾向を-1から1の数値で表します。
計算が非常に複雑なため、手計算で行うことは稀で、統計解析ソフト(RやPythonなど)が使われることが一般的です。Excelで計算するには、非常に複雑なシートを組むか、アドインが必要になります。
計算結果を「散布図」で視覚的に確認しよう
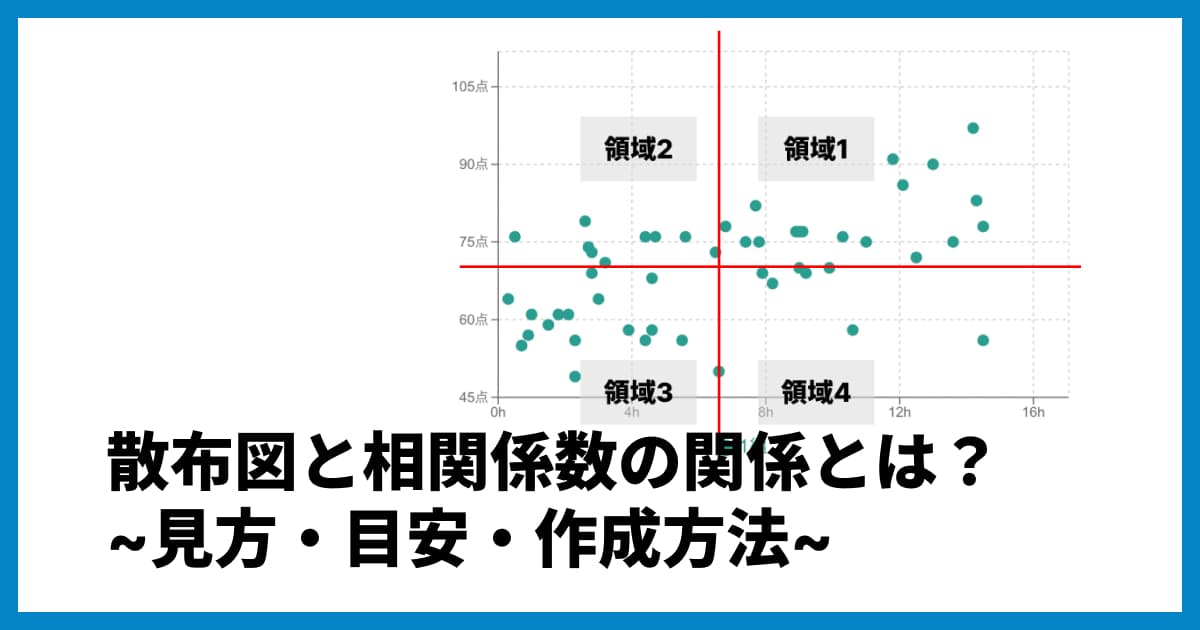
相関係数を計算したら、どの種類の相関係数を使ったかに関わらず、ぜひ散布図も一緒に作成して、データがどのように分布しているかを視覚的に確認しましょう。
なぜなら、相関係数はあくまで「関係性」を一つの数値に要約したものであり、数値だけではデータの全体像を見誤る可能性があるからです。
例えば、ピアソンの相関係数が0.8と出ても、データがきれいな直線上に並んでいるのか、それとも一部の「外れ値」によって数値が引き上げられているのかは、散布図を見ないとわかりません。
また、ピアソンの相関係数が0に近くても、散布図を見たらきれいなU字型の関係(順位相関係数は高くなるかもしれない)が見つかることもあります。
xGrapherで簡単に散布図を作成
「Excelやスプレッドシートを立ち上げるのは少し面倒...」
「もっと手軽にデータを可視化したい」
そんな時は、当サイト「xGrapher」の無料散布図作成ツールが便利です。
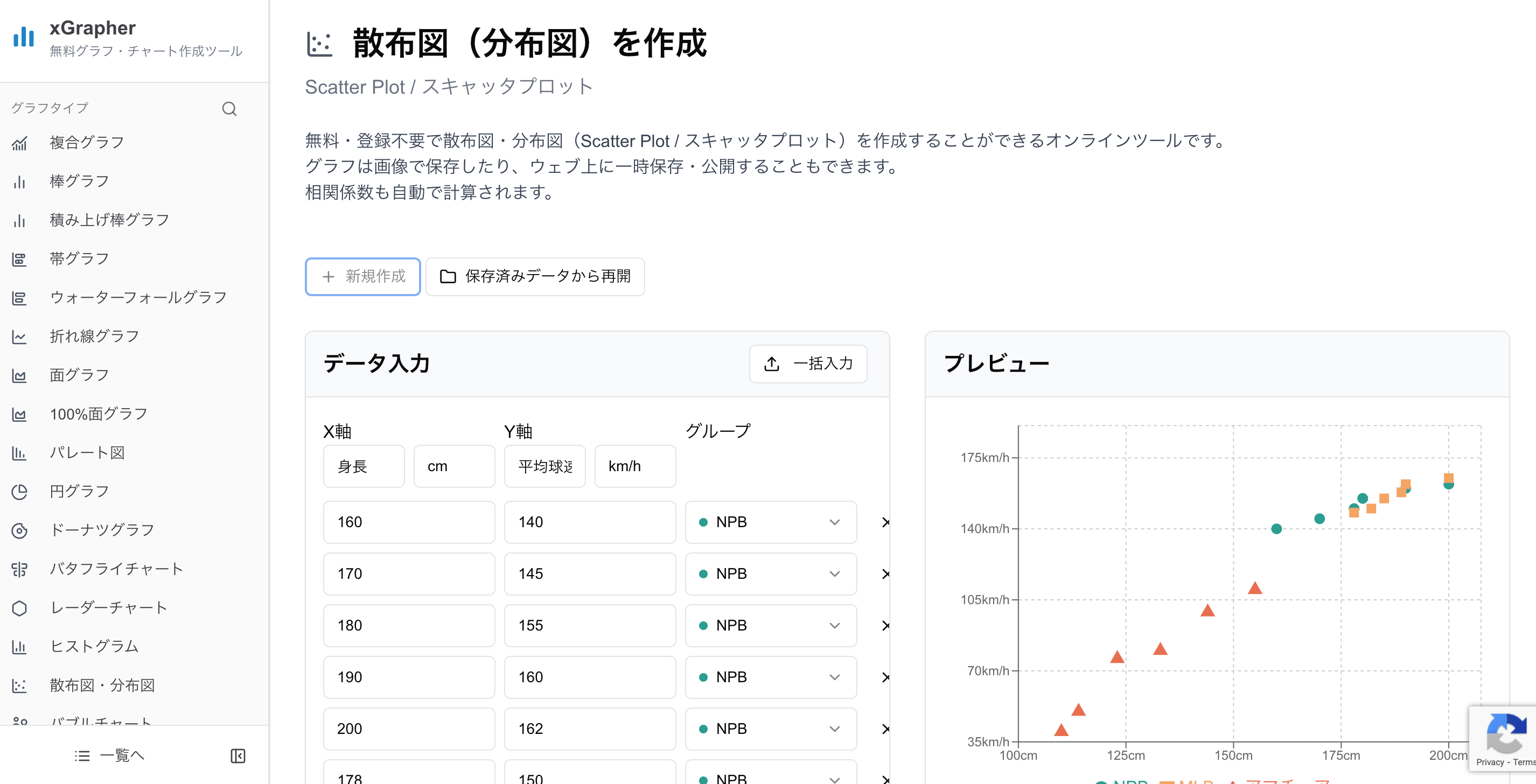
使い方は簡単で、Excelやスプレッドシートのデータをコピーして貼り付けるだけ。
面倒な設定なしに、すぐに美しい散布図が作成され、データがどのような関係にあるかを直感的に把握できます。ピアソンの相関係数 も自動で計算・表示されます。

相関係数を計算するときの注意点
相関係数は便利な指標ですが、使う上で非常に重要な注意点が2つあります。
1. 相関関係は「因果関係」ではない
最も重要な注意点です。相関係数が高い(例:0.8)からといって、「片方が原因で、もう片方が結果である」とは限りません。
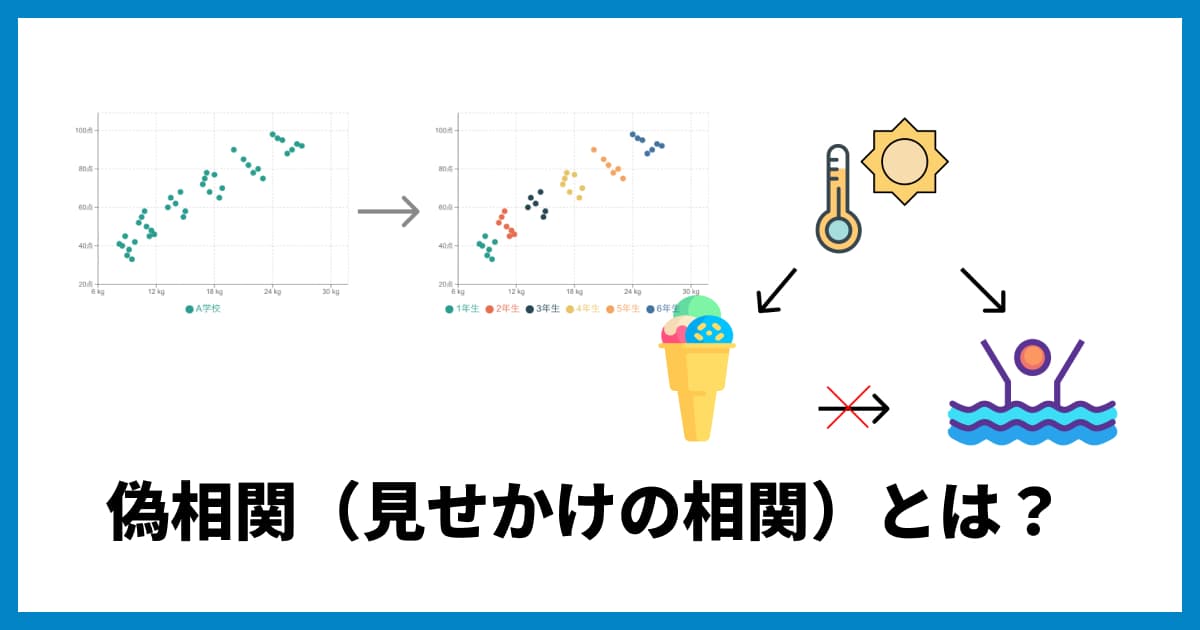
有名な例として、「アイスクリームの売上」と「水難事故の件数」には強い正の相関が見られます。しかし、「アイスが売れるから水難事故が起きる」わけではありませんよね。
これは、「気温が高い」という第3の要因(交絡因子)が、アイスの売上と水難事故の両方を引き起こしているためです(見せかけの相関)。
相関係数はあくまで「関係性があるかもしれない」という仮説のヒントであり、原因と結果を特定するものではないことを覚えておきましょう。
2. 外れ値の影響を大きく受ける(ピアソンの場合)
ピアソンの相関係数は、平均値や標準偏差を使って計算するため、「外れ値」(他のデータから極端に離れた値)があると、その値に引っ張られて相関係数が大きく変わってしまうことがあります。
例えば、ほとんどのデータが無相関(0に近い)でも、たった一つの外れ値があるだけで、相関係数が高く出てしまう場合があります。
だからこそ、計算結果の数値だけを鵜呑みにせず、必ず散布図でデータの分布を確認することが大切です(外れ値の影響が心配な場合は、スピアマンの順位相関係数を試すのも良い方法です)。
また相関係数が偶然の結果かどうかを確認するにはp値を確認する必要があります。
>> 相関係数とp値の意味とは?
まとめ
今回は、相関係数の計算方法について、最も一般的なピアソンの相関係数を中心に、スピアマンやケンドールの順位相関係数にも触れながら解説しました。
ピアソンの相関係数:量的データ間の直線的な関係を測る。Excelの CORREL関数 で簡単。
ピアソンの手計算:「平均→偏差→分散・標準偏差→共分散→相関係数」の順で求める。
スピアマンの順位相関係数:データを順位に変換してからピアソンの計算を行う。外れ値に強い。
ケンドールの順位相関係数:データのペアの順序一致を数える。計算は複雑。
どの相関係数でも、必ず散布図でデータの分布を視覚的に確認することが重要。
相関関係は因果関係ではないことに注意する。
データ分析の第一歩として、相関係数の計算方法と散布図による可視化をマスターし、データに隠された関係性を探ってみましょう。
関連記事:
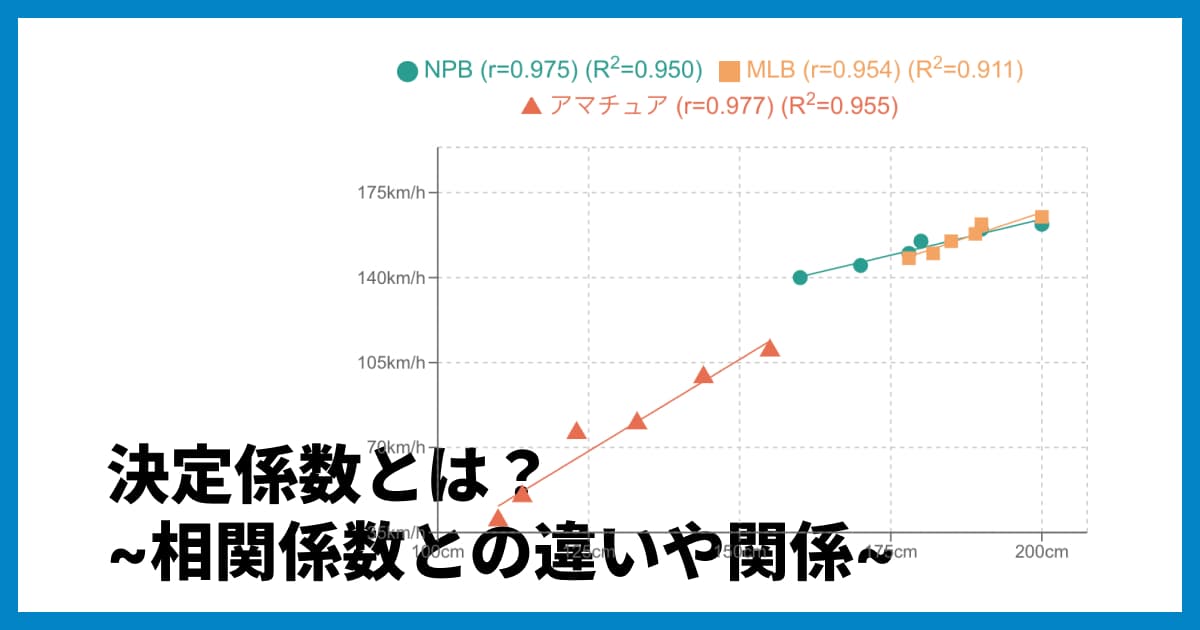
決定係数 (R2) とは?相関係数 (r) との違いや散布図との関係性
Q&A よくある質問
Q1: 相関係数の計算式が複雑で覚えられません。
A1: 無理に暗記する必要はありません。重要なのは「ピアソンの相関係数は、2つのデータがどれだけ一緒に動くか(共分散)を、それぞれのデータのばらつき(標準偏差)で割ったもの」というイメージです。実務ではExcelのCORREL関数や統計ソフトを使うのが一般的ですので、関数の使い方を覚えておけば十分です。
Q2: ピアソン、スピアマン、ケンドールは、どう使い分ければ良いですか?
A2:
ピアソン:身長と体重、売上と広告費など、間隔に意味のある「量的データ」で、直線的な関係を見たい場合に最適です。外れ値には注意が必要です。
スピアマン:「満足度(5段階評価)」や「順位」などの「順序データ」の場合、または量的データでも外れ値の影響を除きたい場合、直線的でなくても単調な関係(増え続ける/減り続ける)を見たい場合に適しています。
ケンドール:スピアマンと同様に「順序データ」に使われますが、特にデータのサンプル数が少ない場合や、順位が同じデータ(タイ)が多い場合に好まれることがあります。計算概念はスピアマンより複雑です。
Q3: 相関係数が0でした。これは「無関係」ということですか?
A3: いいえ、「ピアソンの相関係数」が0の場合、「直線的な関係がない」ことを意味します(無相関)。例えば、データがきれいなU字型(二次関数)に並んでいる場合、2つのデータには強い関係性がありますが、ピアソンの相関係数を計算すると0近くになることがあります。必ず散布図でデータの形を確認してください。
.png)
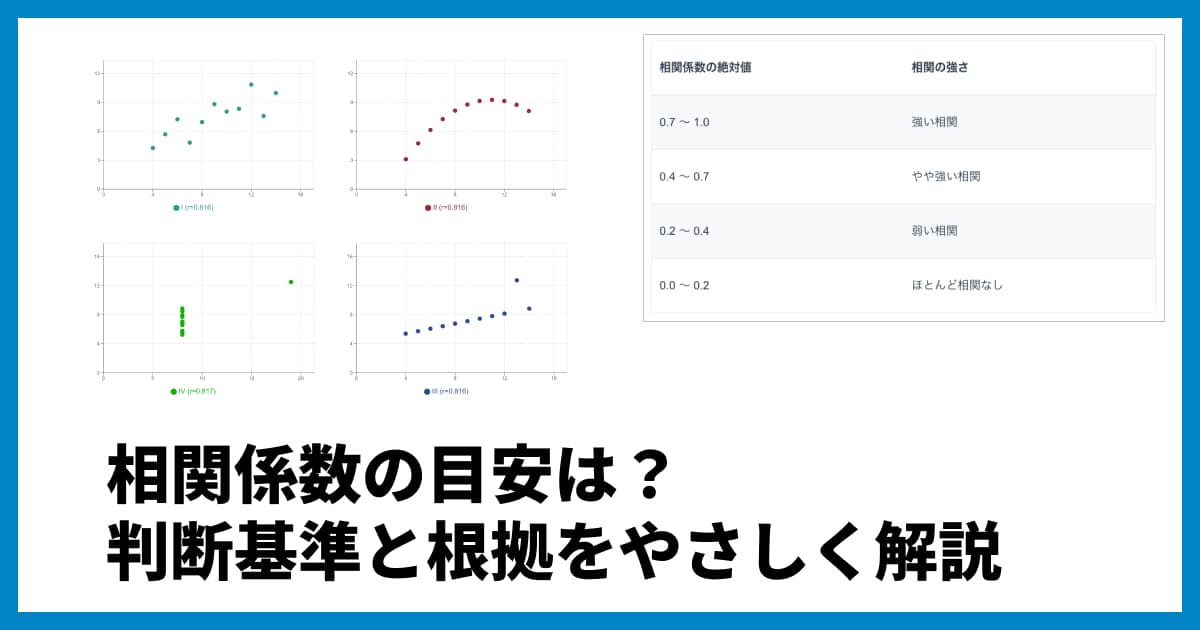
Q4: 相関係数の目安はどれくらいですか?
A4: 分野やデータの性質によって異なりますが、一般的な目安として以下のように解釈されることがあります。
: 強い相関がある
: 中程度の相関がある
: 弱い相関がある
: ほとんど相関がない
(※ は相関係数の絶対値。これはピアソンでも順位相関係数でも概ね共通の目安です)
Q5: Excelでピアソンの相関係数を計算したら #DIV/0! エラーが出ました。なぜですか?
A5: CORREL関数でこのエラーが出る場合、指定したデータ範囲のどちらか(または両方)のデータの値がすべて同じである可能性が高いです。例えば、数学の点数が全員70点だった場合、データのばらつき(標準偏差)が0になります。相関係数の計算式では標準偏差で割り算を行うため、分母が0となり計算エラー(ゼロ除算)が発生します。入力データ範囲や内容を確認してみてください。
)
)
)
)
)
)
)
)
)
)