散布図の相関の見方を徹底解説！相関関係や外れ値の読み取り方

散布図の基本的な見方：3つの相関関係パターン

散布図の見方で最も重要なのが「相関関係（そうかんかんけい）」です。これは、2つのデータの間にどのような関連性があるかを示すもので、主に3つのパターンに分けられます。

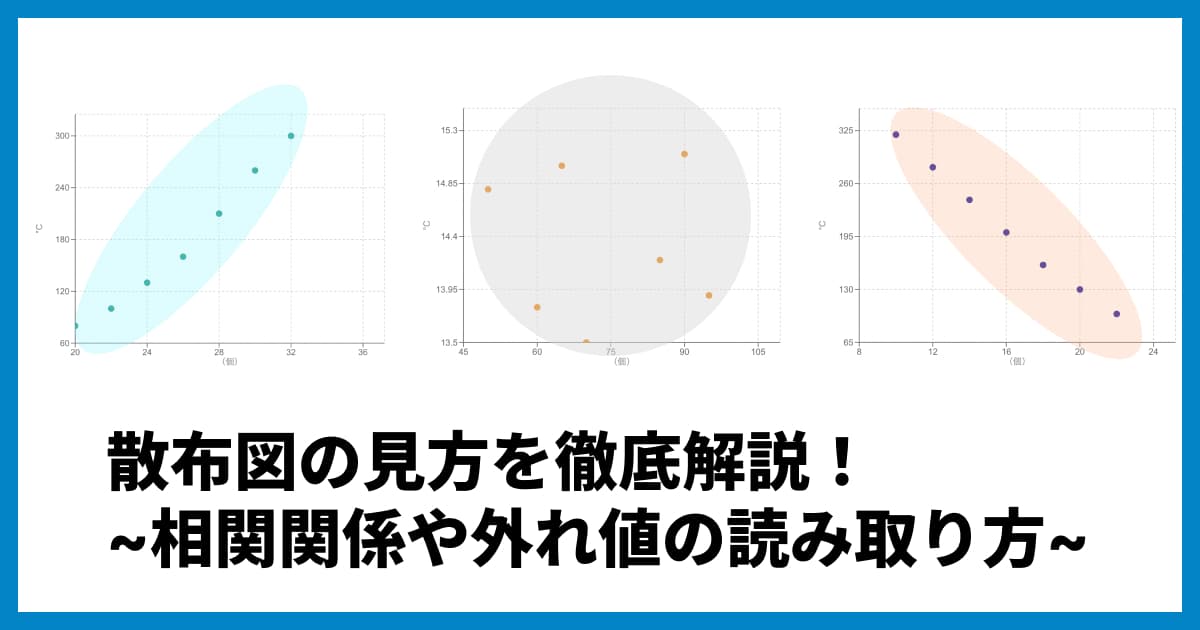
パターン1：正の相関 (右肩上がり)

点が全体的に右肩上がりに分布している場合、それは「正の相関」があることを示します。

これは、片方のデータ（横軸）が増加すると、もう片方のデータ（縦軸）も増加する傾向がある、ということです。

• 例：

  • 気温が上がるほど、アイスクリームの売上も上がる。

  • 勉強時間が長いほど、テストの点数も高くなる傾向がある。

  • 身長が高い人ほど、体重も重くなる傾向がある。

パターン2：負の相関 (右肩下がり)

点が全体的に右肩下がりに分布している場合、それは「負の相関」があることを示します。

これは、片方のデータ（横軸）が増加すると、もう片方のデータ（縦軸）は減少する傾向がある、という逆の関係です。

• 例：

  • 気温が上がるほど、温かい飲み物の売上は下がる。

  • 商品の価格が高いほど、販売数は少なくなる傾向がある。

  • 山の標高が上がるほど、気温は下がる。

パターン3：相関なし (無相関)

点の分布に特定の傾向が見られず、全体にバラバラに散らばっている場合、それは「相関がない（無相関）」ことを示します。

これは、2つのデータの間にはっきりとした関連性が見られない、ということです。

• 例：

  • 数学の点数と、100m走のタイム（必ずしも関係があるとは言えない）。

  • 一日の歩数と、読書量。

もう一歩踏み込む！相関の「強弱」と「外れ値」の見方

相関の「あり・なし」がわかったら、次はその「強さ」と「例外」に注目してみましょう。

点の集まり方で「相関の強弱」を読み取る

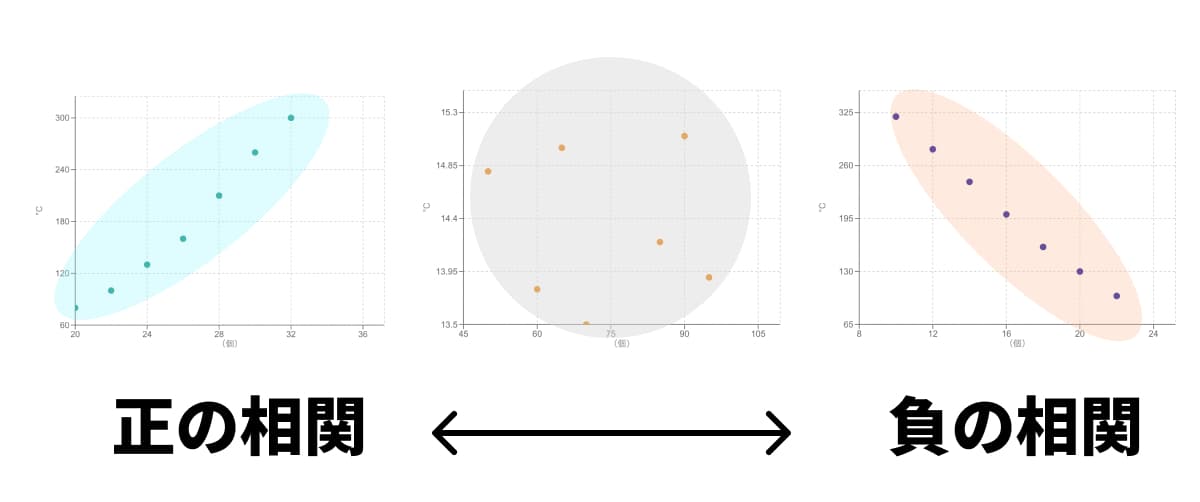
相関関係には「強弱」があります。点の散らばり具合で判断できます。

• 相関が強い：
  点がほぼ一直線上に、細長く集まっている状態です。これは、2つのデータの関連性が非常に高いことを示します。

• 相関が弱い：
  右肩上がりや右肩下がりといった傾向は見えるものの、点が広範囲に（太く）散らばっている状態です。これは、関連性はあるものの、それほど強くない（他の要因も影響している可能性がある）ことを示します。

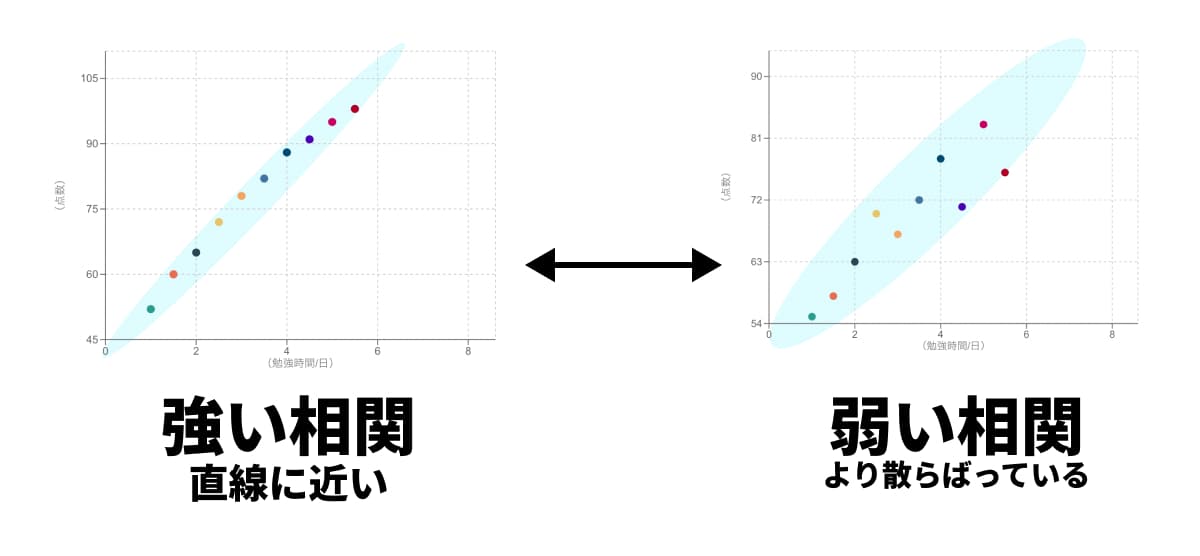
集団から離れた「外れ値」が示す意味

散布図を見ていると、他の多くの点の集まりからポツンと一つだけ離れた点が見つかることがあります。これを「外れ値（はずれち）」と呼びます。

外れ値は、全体の傾向から外れた例外的なデータです。これを見つけたら、「なぜこのデータだけが他と違うのか？」を考えることが重要です。

• 外れ値の例：

  • 勉強時間は短いのに、テストの点数が極端に高い（例：天才肌、またはヤマが当たった）。

  • 広告費を大量に投下したのに、売上が全く伸びていない（例：広告の出し方が悪い、競合が強いキャンペーンを打った）。

  • 単なる測定ミスや入力ミスの可能性。

外れ値は、分析のノイズになることもありますが、時にはビジネスの大きなヒントや改善点（「例外的に売れている理由」など）を示している場合もあります。

散布図を見るときの重要な注意点：「相関関係」≠「因果関係」

散布図を見る上で、最も重要な注意点が一つあります。それは、「相関関係があるからといって、必ずしも因果関係（原因と結果の関係）があるとは限らない」ということです。

例えば、「アイスの売上」と「プールの利用者数」の散布図を作ると、おそらく強い「正の相関」が見られるでしょう（両方とも右肩上がり）。

しかし、「アイスが売れたから（原因）、プールの利用者が増えた（結果）」わけではありませんよね。
この場合、「気温が高い」という共通の原因（第3の要因）が、アイスの売上とプールの利用者数の両方に影響を与えていると考えられます。

このように、2つのデータに関係があるように見えても、それが直接的な原因と結果の関係（因果関係）なのか、それとも裏に別の要因が隠れているのかは、散布図だけでは判断できません。データを深く分析する際には、この点を常に意識しておく必要があります。

相関の強さを数値で見る「相関係数」とは？

散布図の「見た目」だけで判断するのが難しい場合、相関の強さや向きを定量的に（数値で）計算する方法があります。これを「相関係数」と呼びます。 相関係数は -1 から +1 までの値を取り、以下のように解釈されます。

• +1に近いほど: 「強い正の相関」がある（点が右肩上がりの直線に近くなる）

• -1に近いほど:「強い負の相関」がある（点が右肩下がりの直線に近くなる）

• 0に近いほど: 「相関がない」状態（点がバラバラに散らばる）

見た目での判断が曖昧な場合でも、相関係数を計算することで「相関係数が 0.8 なので強い正の相関がある」と客観的に判断できます。ExcelやGoogleスプレッドシートなどの表計算ソフトではCORREL (コレル) 関数を使うと簡単に計算できます。

【応用編】散布図をさらに活用するテクニック

基本的な見方がわかったら、さらに一歩進んだテクニックも見てみましょう。

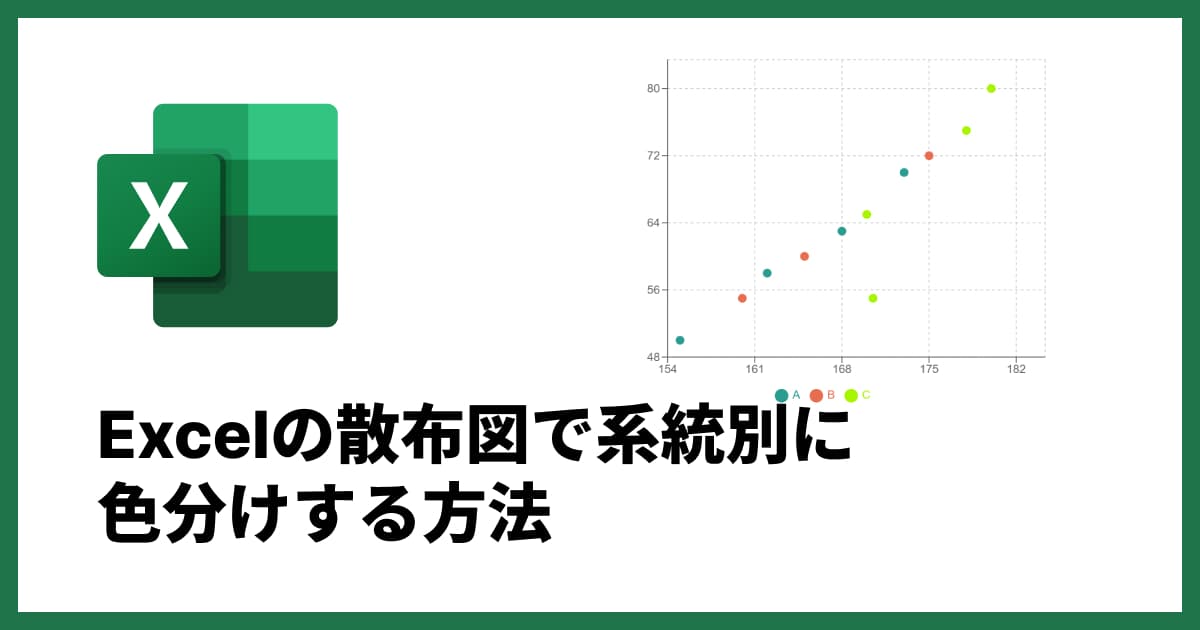
テクニック1：層別（色分け）で隠れた傾向を発見

散布図上の点を、第3のデータ（カテゴリ）で色分けすることを「層別（そうべつ）」といいます。

例えば、「勉強時間（横軸）」と「テストの点数（縦軸）」の散布図を、「クラス別（A組：赤、B組：青）」や「男女別」で色分けしてみます。

すると、全体としては「勉強時間が長いほど点数が高い」という傾向（正の相関）しか見えなかったものが、「A組はB組よりも全体的に点数が高い傾向がある」とか「男子と女子で勉強時間の傾向が違う」といった、より詳細な分析が可能になります。

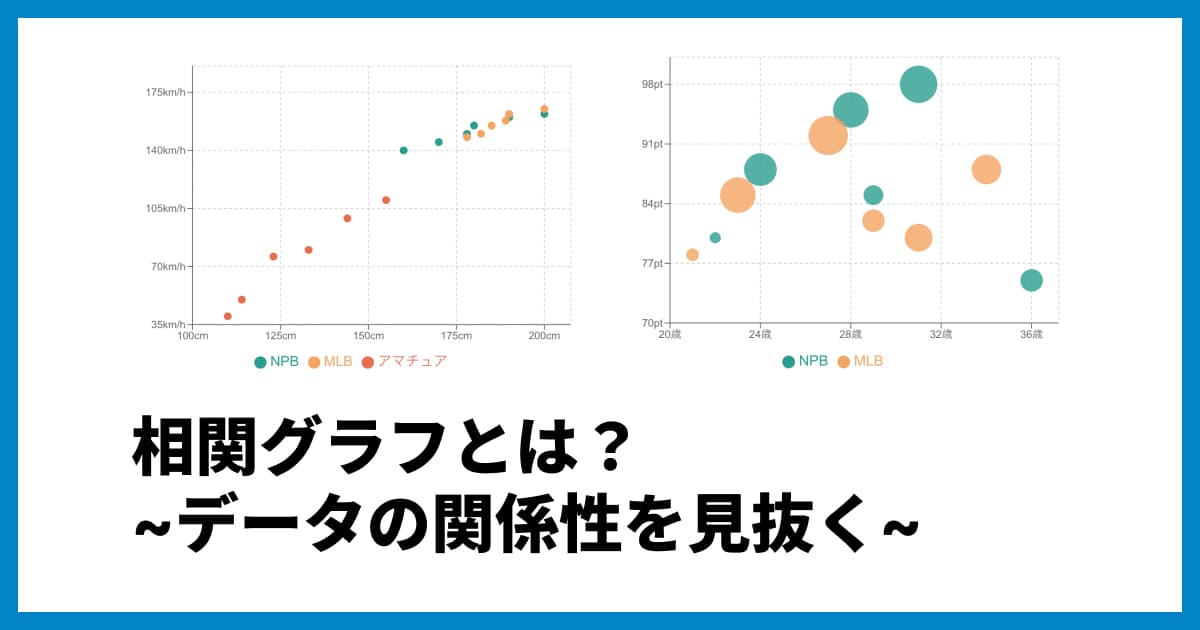
テクニック2：バブルチャートで3つ目の情報を加える

散布図は通常2つのデータ（縦軸・横軸）しか扱えませんが、点の「大きさ」にもう一つの量的なデータ（3つ目のデータ）を割り当てたグラフを「バブルチャート」と呼びます。

例えば、「商品の価格（横軸）」「顧客満足度（縦軸）」に加えて、「売上高（点の大きさ）」をバブルチャートで表現します。
これにより、「価格が安くて満足度が高い商品は、売上も大きい（バブルが大きい）」といった、3つのデータの関係性を同時に読み取ることができます。

• 参考記事： バブルチャート（分布図）とは？見方と作り方がわかる！相関関係の分析や活用事例も解説

オンラインで簡単！xGrapherで散布図を作ってみよう

散布図の見方がわかると、実際に自分で作ってみたくなりますよね。ExcelやGoogleスプレッドシートでも散布図は作成できますが、もっと手軽に、直感的にグラフを作成したい場合は、オンライングラフ作成ツールの利用がおすすめです。

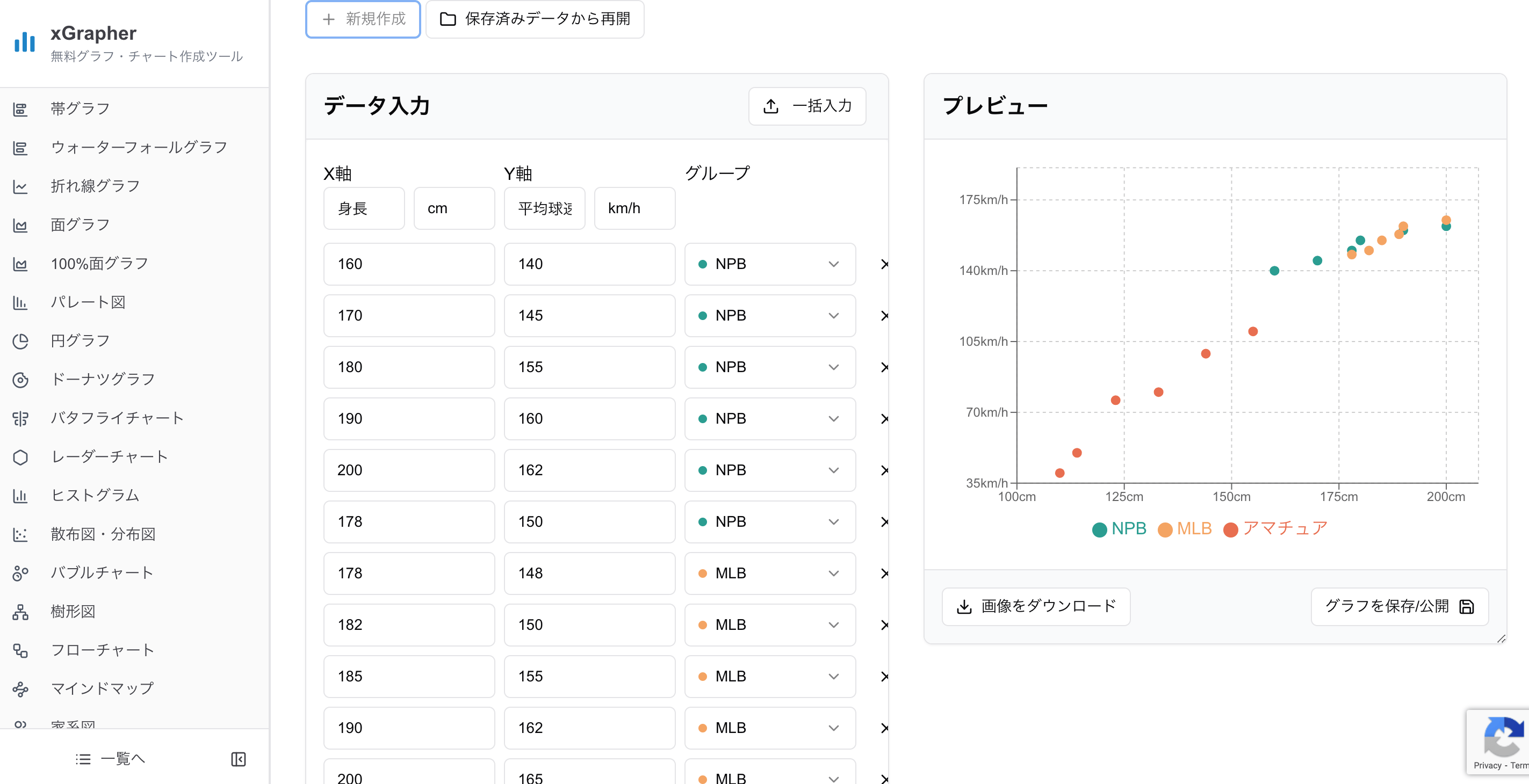
「xGrapher（エックスグラファー）」は、専門的な知識がなくても、データをコピー＆ペーストするだけで、きれいな散布図やバブルチャートをオンラインで簡単に作成できる無料ツールです。

• xGrapherで散布図を今すぐ作成する

• xGrapherでバブルチャートを作成する

データの関係性を可視化したいと思ったら、ぜひxGrapherを試してみてください。

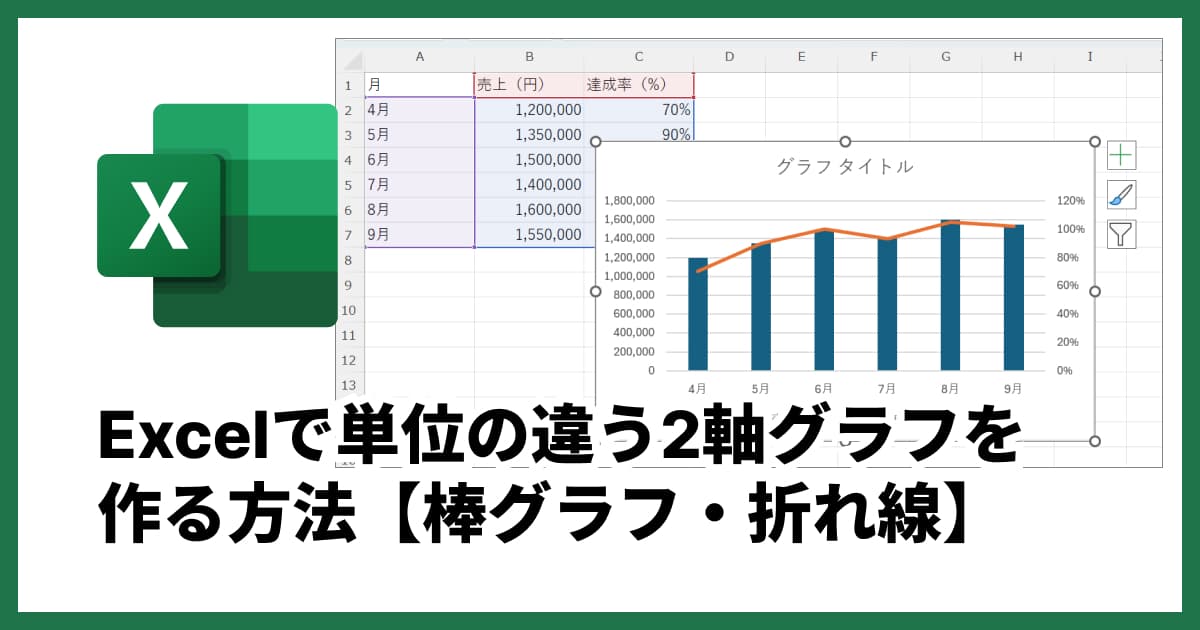
▼xGrapherや各種ツールでの作り方詳細はこちら

• 散布図（分布図）とは？見方と作り方がわかる！相関関係の分析や活用事例も解説

• Excel（エクセル）で散布図を作成する方法を解説！近似曲線の追加方法も

• Googleスプレッドシートで散布図を作成する方法！相関関係の分析にも

「散布図の見方」に関するQ&A

最後に、「散布図の見方」についてよくある質問をまとめました。

Q1. 散布図の点は何を表しているのですか？

A1. 散布図の点は、横軸のデータと縦軸のデータの「組み合わせ」を1つの点としてプロット（打点）したものです。例えば、「ある生徒（点）の、数学の点数（横軸）と英語の点数（縦軸）」のように、2つの情報を1点で示しています。

Q2. 点が一直線に並んでいるのはどういう意味ですか？

A2. 点がほぼ一直線上に並んでいる場合、「非常に強い相関関係」があることを示します。完全に一直線であれば、一方の値が決まればもう一方の値もほぼ予測できる（関数的な関係に近い）ことを意味します。

Q3. 点が縦や横に一直線に並んでいたら？

A3. 点が「縦一直線」に並んでいる場合、横軸の値は同じなのに、縦軸の値だけがバラバラであることを示します。逆に「横一直線」なら、縦軸の値は同じで横軸の値だけがバラバラということです。これらは通常「相関なし」と解釈されます。

Q4. 散布図は何のために使うのですか？

A4. 主に「2つのデータの関係性を確認するため」や「傾向から外れた例外的なデータ（外れ値）を見つけるため」に使われます。ビジネスでは、売上と広告費の関係分析、品質管理（不良品の発生要因調査）などでよく活用されます。

Q5. 散布図とバブルチャートの違いは何ですか？

A5. 散布図は2つのデータ（縦軸・横軸）の関係性を見ますが、バブルチャートはそれに加えて第3のデータ（量）を「点の大きさ（バブルの大きさ）」で表現します。つまり、バブルチャートは3つのデータの関係性を同時に見られる、散布図の応用的なグラフです。