相関係数の目安は?0.7なら強い?弱い?判断基準と根拠をやさしく解説
データ分析をしていると、「相関係数」を計算する場面はよくありますよね。「とりあえず計算してみたけど、このという数字は、結局『相関がある』と言っていいの?」「を超えたから『強い相関』って聞くけど、それって本当?」「そもそも、その目安って誰が決めたの?」
こんな疑問を持ったことはありませんか?
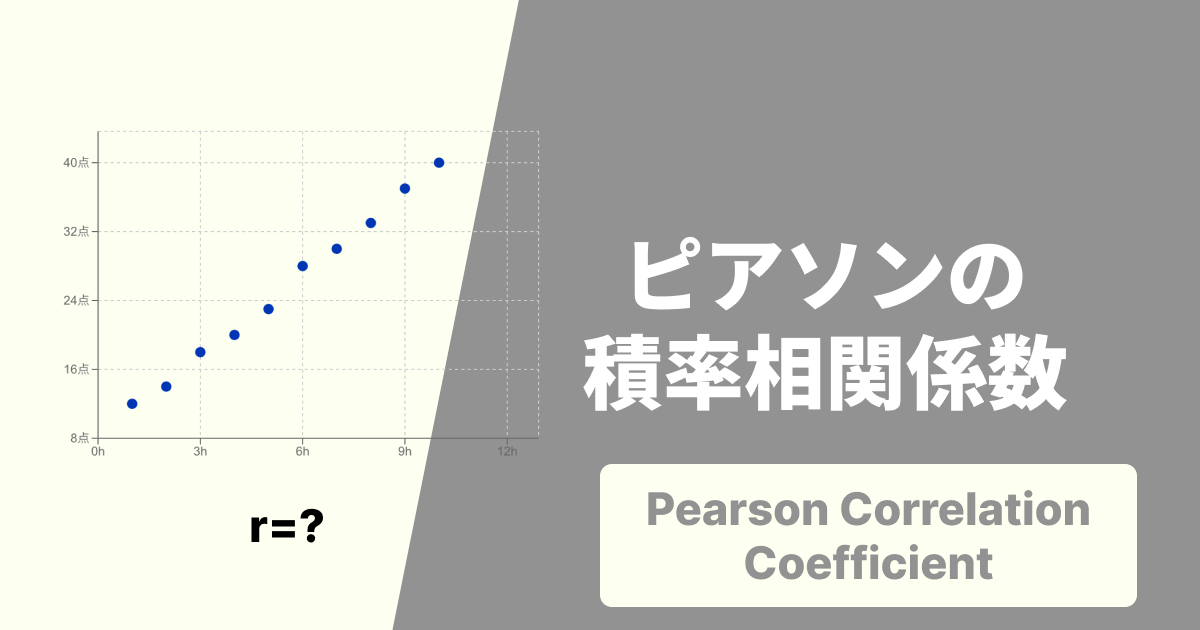
相関係数は、-1から+1までの値で、2つのデータ間の直線的な関係の強さを示します。便利ですが、その数字だけを見て「0.8だからOK!」「0.3だからダメだ…」と機械的に判断するのは、実はとても危険です。
この記事では、相関係数の値を解釈するための一般的な「目安」と、その目安がなぜ使われるのかという「根拠」、そして目安を使う上での大切な注意点について、分かりやすく解説していきます。
この記事の内容(目次)
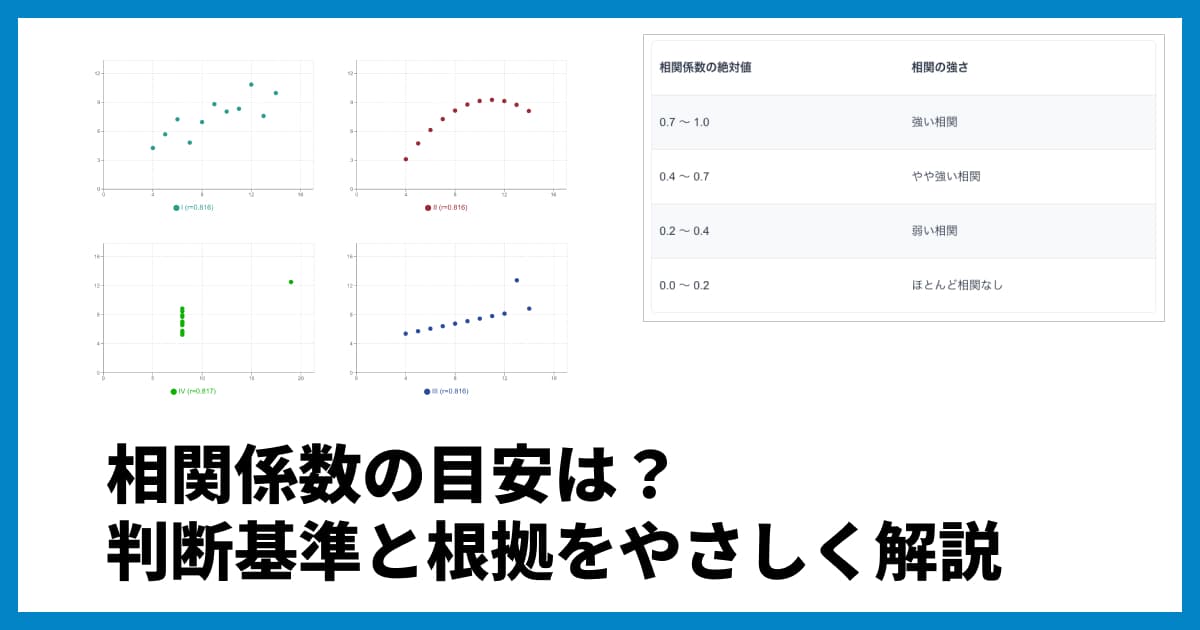
一般的に使われる相関係数の目安
相関係数(ピアソンの積率相関係数を指すことが多いです)の強さを判断する目安として、よく引用される基準があります。これはあくまで「慣習的な目安」であり、分野や目的によって解釈が異なる点に注意が必要ですが、ひとまずの基準として広く知られています。
相関係数の絶対値 | 相関の強さ |
0.7 〜 1.0 | 強い相関 |
0.4 〜 0.7 | やや強い相関 |
0.2 〜 0.4 | 弱い相関 |
0.0 〜 0.2 | ほとんど相関なし |
ポイント:
相関係数はプラス()とマイナス()の符号を持ちます。
プラス()は「片方が増えると、もう片方も増える」傾向がある正の相関を示します。(例: 身長と体重)
マイナス()は「片方が増えると、もう片方は減る」傾向がある負の相関を示します。(例: 勉強時間とゲーム時間)
上記の表は、符号を外した絶対値 での目安です。 も も、「相関の強さ」としては同じ「強い相関」と解釈されます。
なぜこの目安なの?その「根拠」とは
では、なぜ「以上が強い」「が中間」といった目安が使われるのでしょうか。これには、統計学的な背景や経験則が関わっています。
根拠1:説明力の強さ(決定係数 )
相関係数を2乗した値()を決定係数(または寄与率)と呼びます。これは「片方のデータ(説明変数)の変動のうち、もう片方のデータ(目的変数)の変動によってどれくらい説明できるか」を示す割合(%)を表します。
もし なら、()。一方の変動を100%説明できる、完全な関係です。
もし なら、()。一方の変動の約半分(49%)を、もう一方で説明できることを意味します。
もし なら、()。16%しか説明できません。
もし なら、()。ほとんど説明できていません。
このように考えると、「」は変動の約半分を説明できるラインであり、「強い」相関と呼ぶ一つの節目として捉えやすいことが分かります。「」では程度であり、「強い」とは言い難いですよね。
(※ここに、横軸を(0-1)、縦軸を(0〜1)としたのグラフを配置し、で、でとなる点に目印を付けると分かりやすいです)
根拠2:統計的検定と「値」
相関係数が「たまたまその値になった」だけなのか、それとも「統計的に意味のある(有意な)関係」なのかを判断するために、統計的検定(無相関検定)を行います。
この検定では「本当は相関がない(r=0)のに、偶然0から離れた値が出た確率」をp値として計算します。一般的に p値が5%(0.05)未満であれば、「偶然とは考えにくい、統計的に有意な相関がある」と判断します。
(より詳細な相関係数の計算や検定については「相関係数とは?見方や計算方法、Excelでの求め方を解説」も参考にしてください。)
根拠3:研究分野ごとの「経験則」
実は、相関係数の目安は、分野によって大きく異なります。
自然科学(物理学、化学など):
測定誤差が少ない実験データでは、以上でないと「強い相関」とは見なされないことも多いです。社会科学(心理学、経済学、マーケティングなど):
人間の行動や社会現象など、多くの要因が複雑に絡み合うデータを扱います。そのため、測定誤差も大きくなりがちで、程度でも「意味のある中程度の相関」と解釈されたり、でも「弱いながらも関係性が見られる」と考察されたりすることがあります。
つまり、よく言われる「が強い」という目安は、社会科学分野などにおける経験則的な基準である側面が強いのです。
超重要!相関係数の目安を使う際の3つの注意点
相関係数の目安は便利ですが、数字だけを見て判断すると大きな間違いを犯す可能性があります。以下の点に必ず注意してください。
注意点1:必ず「散布図」で可視化する
これは最も重要な注意点です。相関係数は、あくまで2つのデータの「直線的な」関係の強さしか測れません。
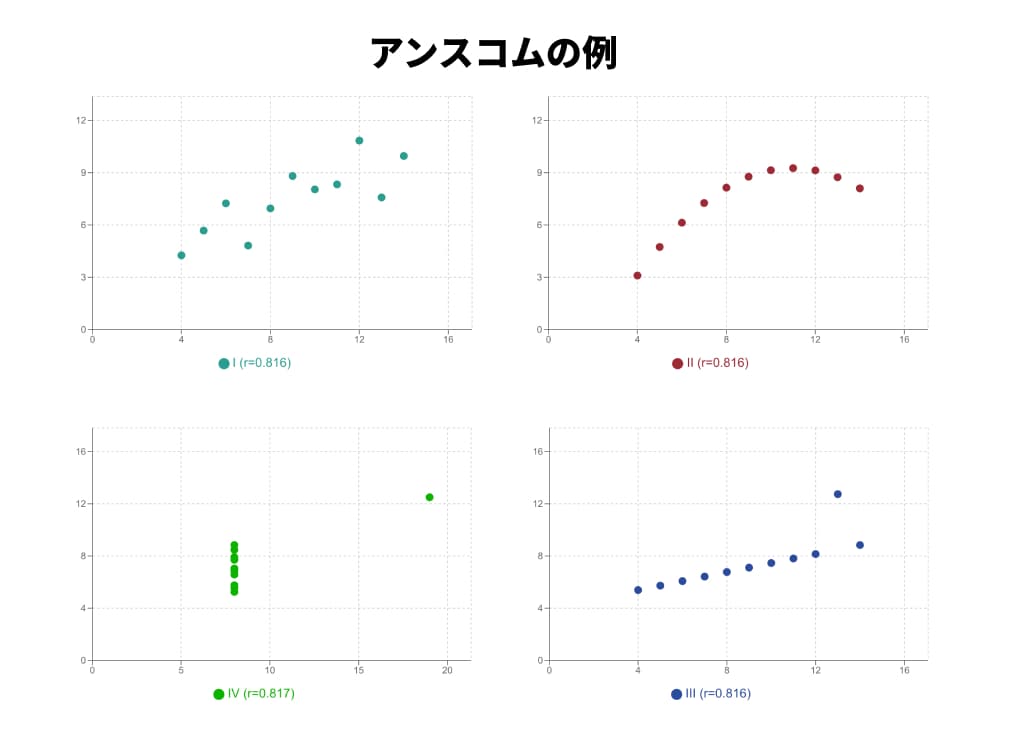
上の図(アンスコムの例と呼ばれます)は驚くべきことに、これら4つのデータセットは、平均、分散、そして相関係数r(約)がほぼ全て同じなのです。
相関係数の値だけ見れば「強い正の相関」ですが、実際のデータ(散布図)を見ると、
(左上) きれいな直線関係
(右上) きれいな曲線関係(直線ではない!)
(左下) ほぼ直線だが、1点だけ外れ値がある
(右下) ほとんどが無関係だが、1点だけの外れ値が相関係数を引き上げている
と、その中身は全く異なります。
もし(右上)のデータで「だから強い直線関係だ」と結論付けたら、それは完全な間違いです。
相関係数を計算したら、必ず散布図を描いて、目で見て確認する癖をつけましょう。
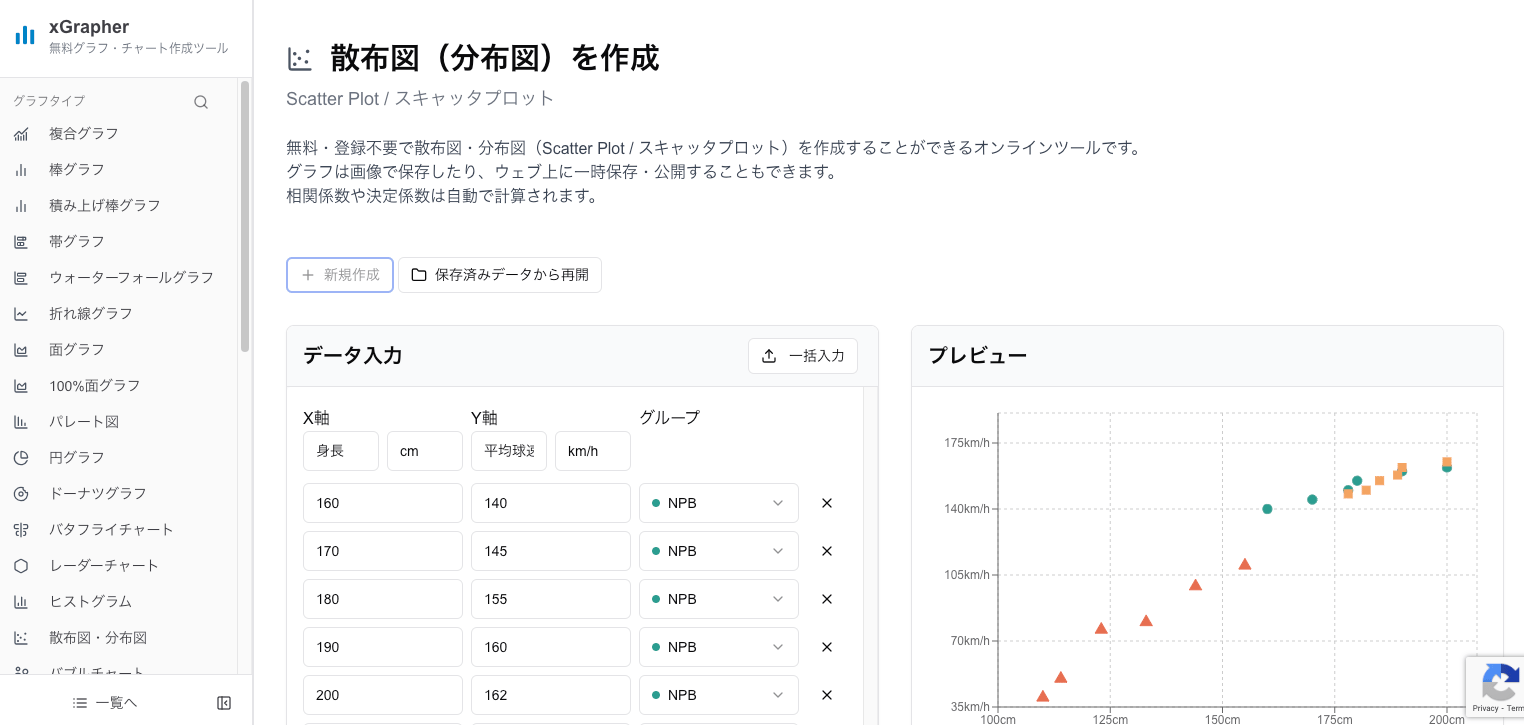
オンラインツールの「xGrapher 散布図作成ツール」を使えば、データをコピー&ペーストするだけですぐに散布図を作成し、相関係数も同時に確認できます。
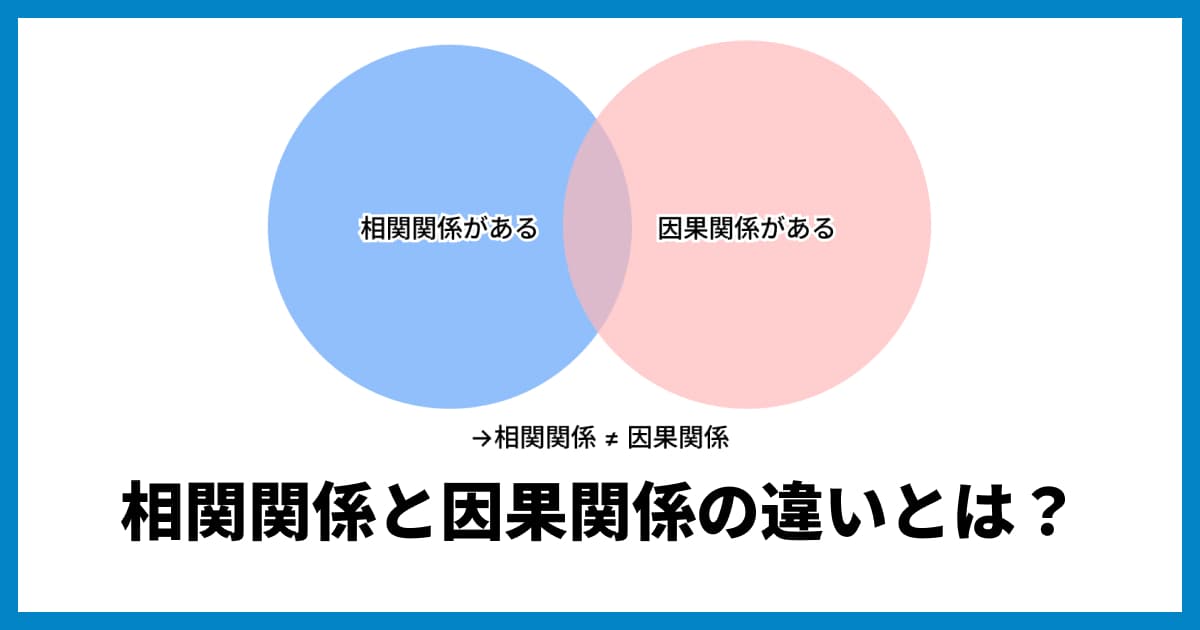
注意点2:「相関関係」は「因果関係」ではない
「の強い相関がある」からといって、「片方が原因で、もう片方が結果だ」と結論付けることは絶対にできません。
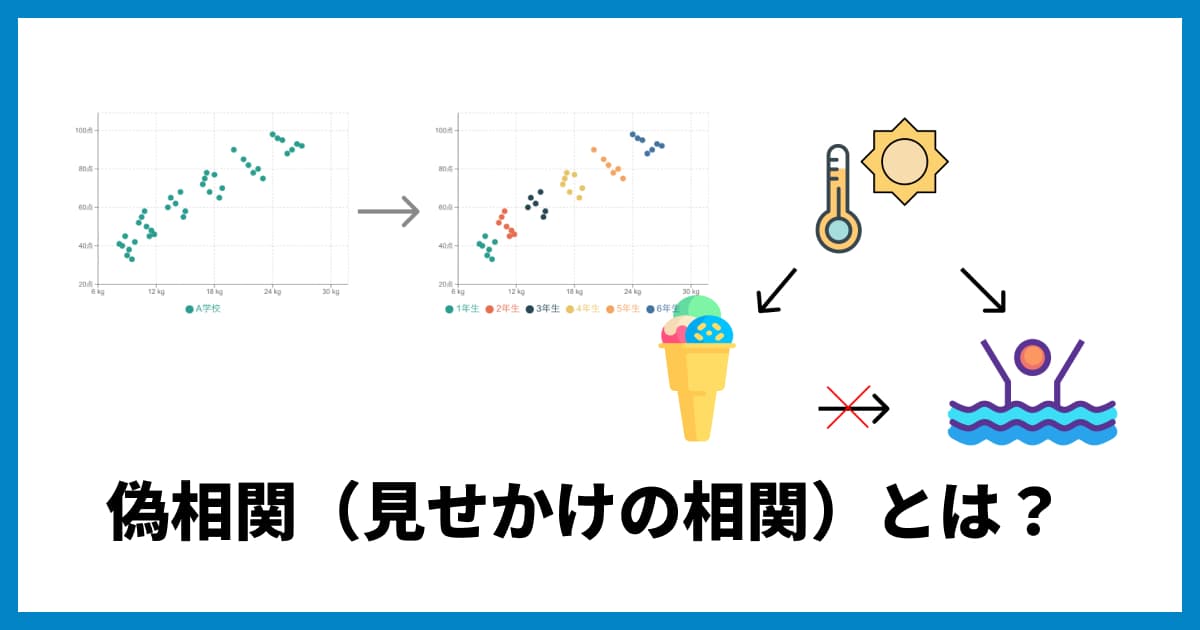
有名な例に、「アイスクリームの売上」と「水難事故の件数」があります。この2つには強い正の相関が見られます。
しかし、「アイスが売れると(原因)、水難事故が増える(結果)」のでしょうか?違いますよね。
.jpg)
これは「気温が高い」という第3の要因(交絡因子)が両方に影響しているためです。
気温が高い → アイスが売れる
気温が高い → 海やプールに行く人が増え、水難事故が増える
このように、2つのデータの間に見かけ上の相関(疑似相関)が生まれることはよくあります。相関係数は、因果関係を証明するものでは決してないことを肝に銘じてください。
>> 相関関係と因果関係の違いとは?データ分析で間違う前に知りたい基本
注意点3:データの「外れ値」に注意する
注意点1の(左下)や(右下)の例のように、たった1つの「外れ値」データが、相関係数の値を大きく変えてしまうことがあります。
データ入力のミスなのか、それとも異常値として意味のあるデータなのかを検討し、必要に応じて外れ値を除外して再計算するなどの対応も必要です。
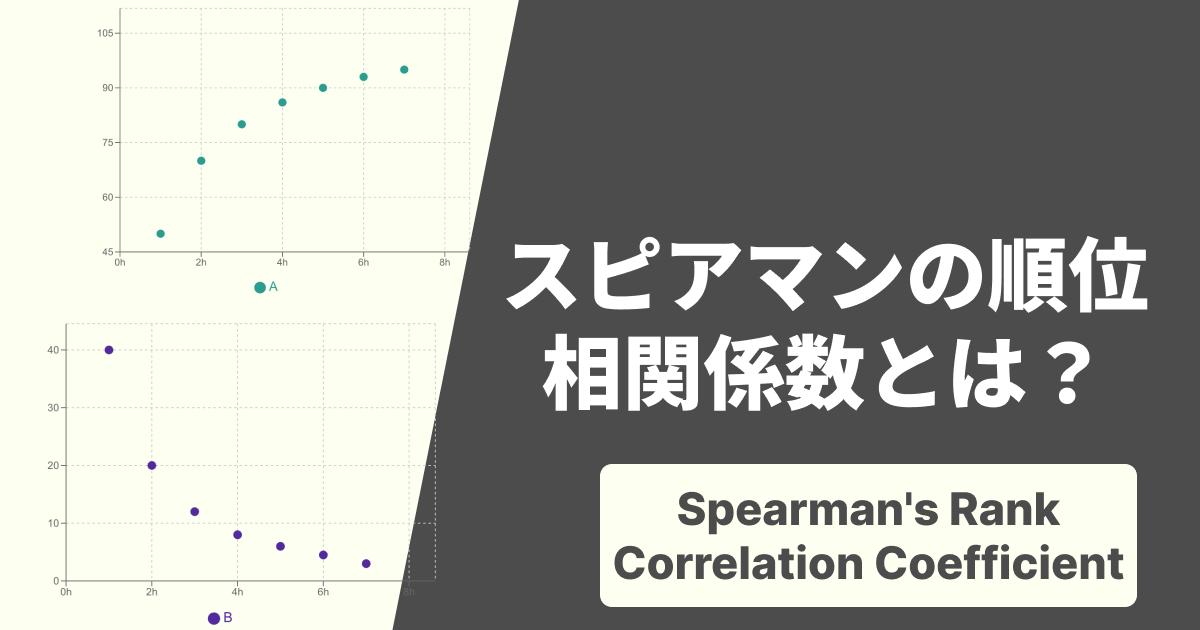
ピアソン以外も!相関係数の種類
ここまで説明してきたのは、主に「ピアソンの積率相関係数」です。これは2つのデータが両方とも「間隔尺度・比率尺度」(身長、体重、温度、金額など)の場合に使われます。
データが「順序尺度」(好き嫌いの順位、満足度ランキングなど)の場合は、ピアソンではなく「スピアマンの順位相関係数」や「ケンドールの順位相関係数(ケンドールのタウ)」を使う必要があります。
※詳しくは「スピアマンの順位相関係数とは」「ケンドールの順位相関係数(タウ)とは」を参照してください。
これらの相関係数も-1から+1の値をとりますが、ピアソンとは計算方法が異なるため、解釈の目安も厳密には異なります。ただし、強さの感覚としては、ピアソンの目安を参考にしても大きくは外れません。
まとめ:相関係数の目安は「参考」にしかならない
相関係数の目安について、その根拠や注意点を解説してきました。
一般的に「」で強い相関、「」で中程度の相関、「」で弱い相関と言われることが多い。
その根拠は、決定係数()で「変動の約半分を説明できる」のが であることや、分野ごとの経験則に基づいている。
最重要:目安は絶対ではない!
必ず散布図で可視化し、直線関係か、外れ値はないかを確認する。(xGrapher 散布図作成ツール)
相関関係は因果関係ではないことを忘れない。
分野によって「強い」の基準は異なることを理解する。
相関係数は便利な指標ですが、その数字に振り回されてはいけません。必ずデータの背景や散布図とセットで解釈するようにしましょう。
相関係数の目安に関するQ&A
Q1: 相関係数が0.5でした。これは「相関あり」と言っていいですか?
A1: は、一般的な目安では「中程度の相関(やや相関あり)」と解釈されます。ただし、これが統計的に意味のある(有意な)相関かどうかは、データ数にも依存するため、値を確認する必要があります。また、分野によってはを「強い」と見なす場合もあれば、「弱い」と見なす場合もあります。
Q2: 相関係数が0.1でした。これは「無関係」ということですか?
A2: は、目安では「ほとんど相関がない」に近い値です。直線的な関係はほぼ無いと言えます。ただし、散布図を描いてみると「U字型」のような曲線関係が隠れている可能性もゼロではありません。
Q3: 相関係数の目安に、法的な決まりや学会の統一基準はありますか?
A3: ありません。この記事で紹介した目安()は、あくまで慣習的・教育的に広く使われている一例です。統計学者のギルフォードによる基準など、提唱者によっても具体的な数値は異なります。
Q4: マイナスの相関(例: )は、プラスの相関(例: )より「弱い」ですか?
A4: いいえ、「強い」です。相関の「強さ」は絶対値 で見ます。 であり、 です。 なので、 の方が よりも「強い」相関関係(強い負の相関)を示しています。
Q5: 相関係数を正しく理解するために、目安以外で何を見れば良いですか?
A5: 最も重要なのは「散布図」です。データの分布、直線からのばらつき、外れ値の有無を視覚的に確認してください。次に、データ数が十分か、統計的に有意か(値)、そして因果関係と混同していないか、をチェックすることが重要です。
(散布図の見方については「散布図と相関係数の関係」「散布図の相関の見方」も役立ちます。)
)
)
)
)
)
)
)
)
)