散布図と相関係数の関係とは？見方と目安、作成方法まで徹底解説

散布図とは？ 2つのデータの関係性を目で見るグラフ

散布図（さんぷず）は、2つの項目（変数）のデータを点でプロットしたグラフです。横軸（X軸）と縦軸（Y軸）にそれぞれ異なるデータを割り当て、対応する値の場所に点を打っていきます。

例えば、クラス全員の「勉強時間（横軸）」と「テストの点数（縦軸）」を散布図にすると、点がどのように分布しているかで、2つの関係性の大まかな傾向が見えてきます。「勉強時間が多い人ほど、テストの点数も高い」傾向があれば、点は右肩上がりに集まるでしょう。

散布図の主な目的は、2つのデータ間に何らかの関連性（相関関係）があるかを視覚的に把握することです。

(※散布図の基本的な作り方や種類については、こちらの記事「散布図とは？基本的な見方から作成時のポイントまで」でも詳しく解説しています。)

相関係数とは？ 関係性の「強さ」と「向き」を数値化

散布図で「なんとなく関係ありそう」とわかったら、次に知りたくなるのが「どれくらい強く関係しているのか？」です。それを客観的な数値で示してくれるのが相関係数（correlation coefficient）です。

相関係数は、-1から1までの間の値をとります。

• 1に近い（例: 0.8, 0.9）: 非常に強い正の相関がある。一方が増えると、もう一方も増える傾向が強い。（例: 勉強時間と点数）

• -1に近い（例: -0.7, -0.9）: 非常に強い負の相関がある。一方が増えると、もう一方は減る傾向が強い。（例: 運動時間と体脂肪率）

• 0に近い（例: -0.1, 0, 0.2）: ほとんど相関がない（無相関）。2つのデータに関連性が見られない。

>> 相関係数の目安とその根拠についての解説

相関係数の主な種類

一口に「相関係数」と言っても、データの性質によって使い分ける必要があります。

1. ピアソンの積率相関係数 (Pearson's r)

最も一般的に使われる相関係数で、単に「相関係数」と言う場合、通常はこれを指します。「勉強時間」と「テストの点数」のような量的データ間の直線的な関係を測るのに使われます。この記事で主に解説しているのは、このピアソンの相関係数です。

2. スピアマンの順位相関係数 (Spearman's ρ)

データを数値そのものではなく、「順位」（ランキング）に変換してから計算する相関係数です。

「満足度（5段階評価）」や「成績の順位」といった順序データに使えます。また、外れ値（極端に離れた値）の影響を受けにくい、直線でなくても「一方が増えれば、もう一方も（おおむね）増える」（単調関係）という傾向も捉えられる、といった特徴があります。

>> スピアマンの順位相関係数とは？ピアソンとの違いなどわかりやすく解説

3. ケンドールの順位相関係数 (Kendall's τ)

スピアマンと同様に、順位に基づいて計算されます。データのペアの順序が一致しているか（増加傾向か）、逆転しているか（減少傾向か）に着目して計算される指標です。

>> ケンドールの順位相関係数 ($\tau$)とは？計算方法も紹介

相関係数の計算方法（基本的な考え方）

「相関係数の数値はどうやって決まるの？」と疑問に思うかもしれません。

>> 相関係数の計算方法の解説記事はこちら

実際の計算式は複雑ですが、その「考え方」は散布図を見ると理解しやすくなります。

ここでは、ピアソンの相関係数がどのように「プラス」や「マイナス」を判断しているのか、その基本的な仕組みを紹介します。

ステップ1: データの「中心（平均）」を見つける

まず、全データの「X軸の平均値」と「Y軸の平均値」を計算し、グラフに中心線（平均線）を引きます。

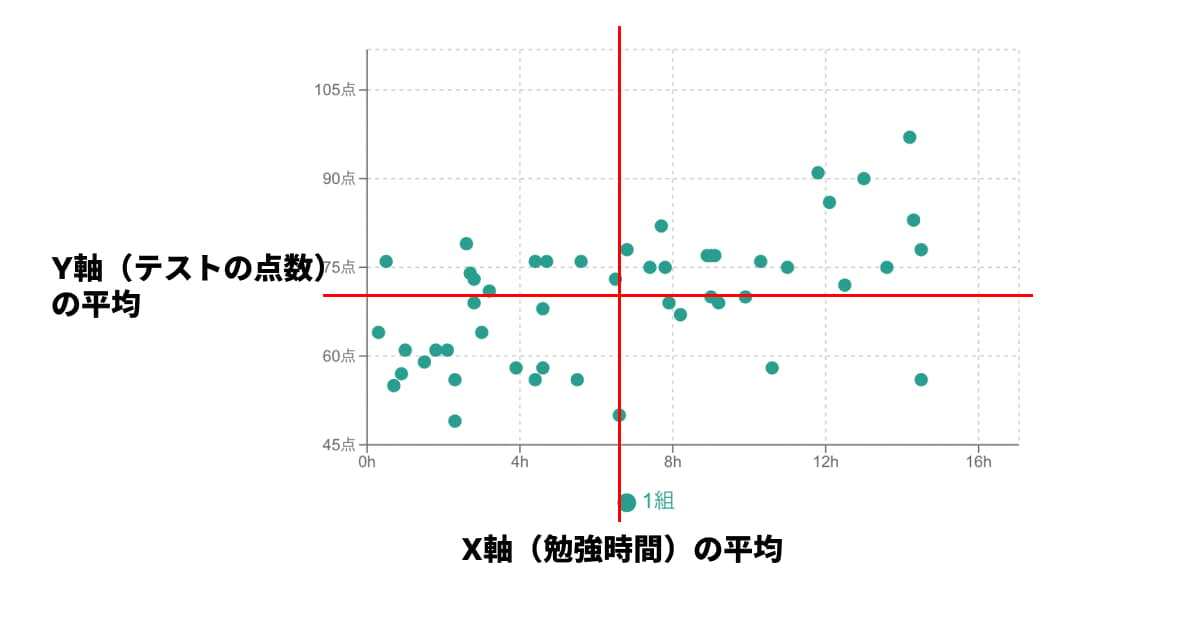
ステップ2: グラフを4つの領域に分ける

この2本の平均線によって、散布図は4つの領域（象限）に分割されます。

• 領域1 (右上): Xが平均より大きく、Yも平均より大きい（＋, ＋）

• 領域2 (左上): Xが平均より小さく、Yは平均より大きい（－, ＋）

• 領域3 (左下): Xが平均より小さく、Yも平均より小さい（－, －）

• 領域4 (右下): Xが平均より大きく、Yは平均より小さい（＋, －）

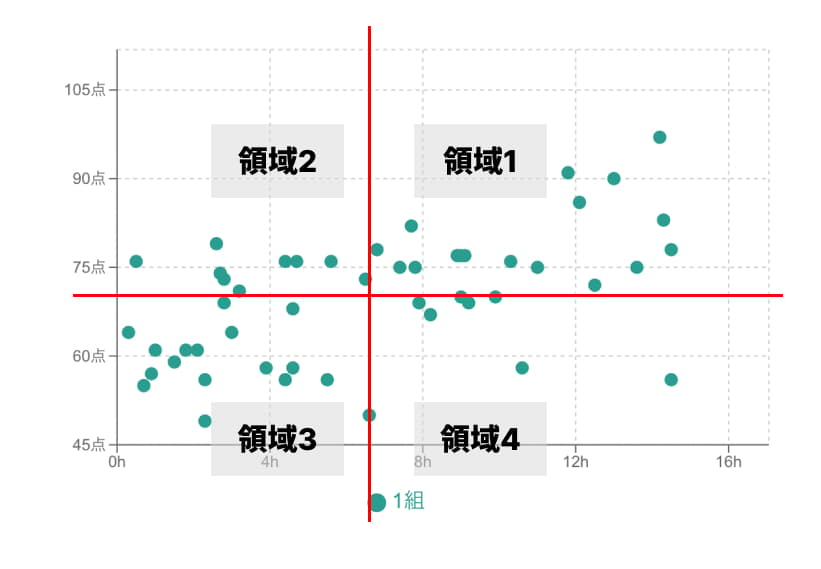
ステップ3: 点の分布を見る

相関係数は、これらの領域に点がどれだけ集まっているかで決まります。

• 正の相関が強くなる場合:

  多くの点が「領域1 (右上)」と「領域3 (左下)」に集まります。

  (＋, ＋) のペアと (－, －) のペアが多い（＝同じ符号のペアが多い）と、計算結果は大きなプラスになります。

• 負の相関が強くなる場合:

  多くの点が「領域2 (左上)」と「領域4 (右下)」に集まります。

  (－, ＋) のペアと (＋, －) のペアが多い（＝異なる符号のペアが多い）と、計算結果は大きなマイナスになります。

• 相関が0に近くなる場合:

  4つの領域に点が均等に散らばっている場合、プラスの力とマイナスの力が打ち消し合い、相関係数は0に近づきます。

このように、相関係数は「データが平均から見て、どの領域にどれだけ集まっているか」を数値化したものなのです。

【図解】散布図のパターンと相関係数の目安

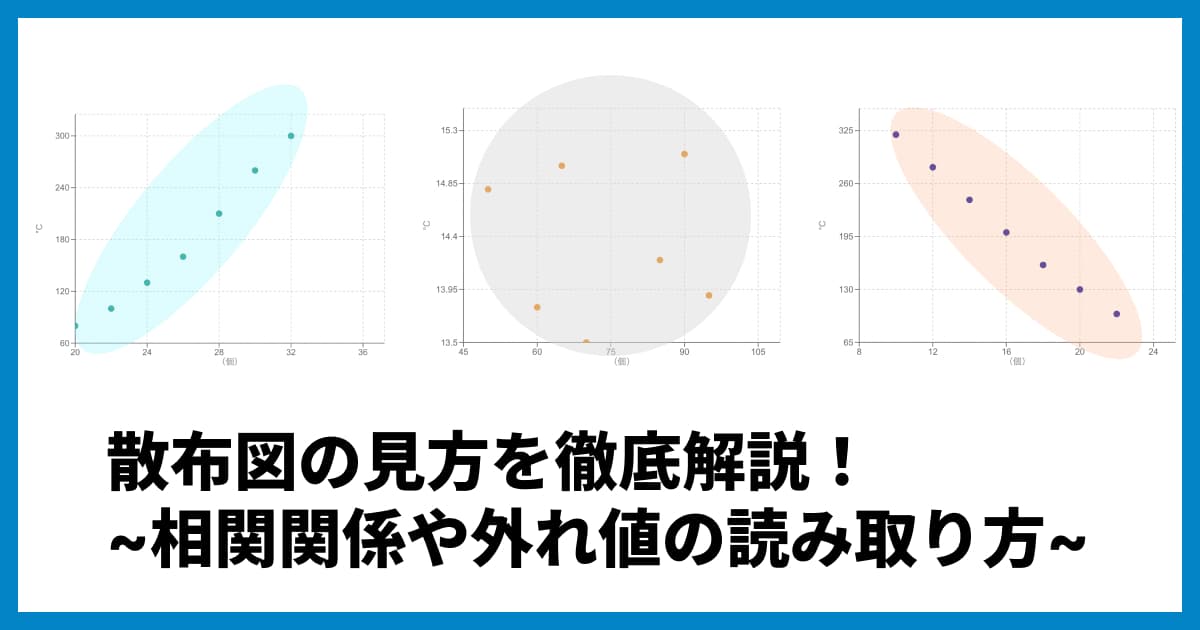
散布図の点の散らばり具合（パターン）と、相関係数の値には密接な関係があります。実際のデータ分析では、両方をセットで確認することが非常に重要です。

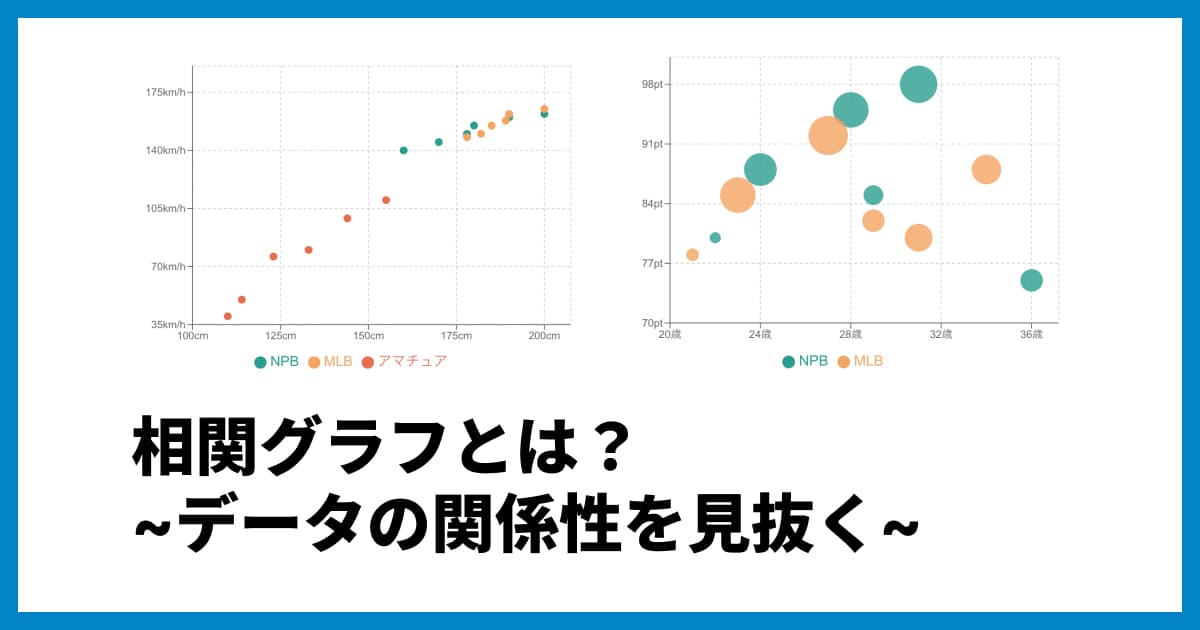
1. 強い正の相関（0.8~1.0）

点がほぼ一直線上に、くっきりと右肩上がりに並びます。片方が増えれば、もう片方もほぼ確実に増える関係です。（例: 野球選手の身長と球速）

2. 弱い正の相関（0.3~0.5）

全体として「なんとなく右肩上がりかな？」と見える程度で、点のばらつきが大きくなります。傾向はあるものの、例外も多い状態です。（例: 勉強時間とテストの点数）

3. 強い負の相関 (-0.8~-1.0)

点がほぼ一直線上に、くっきりと右肩下がりに並びます。片方が増えれば、もう片方はほぼ確実に減る関係です。（例: 中古車の買取価格と経過年数の関係など）

4. ほぼ無相関 (相関係数 0)

点が円形や特定のパターンなくランダムに散らばっており、明確な傾向（右肩上がり/下がり）が見られません。2つのデータに関連性はありません。（例: 靴のサイズと月の読書冊数）

相関係数の目安（一般的な解釈）

相関の強さの解釈は分野によって異なりますが、一般的な目安は以下の通りです。

>> 相関関数の目安やその根拠についての解説

(※散布図の詳しい見方やパターンについては、「散布図の見方をマスター！相関関係のパターンを読み解く」も参考にしてください。)

相関係数を読み解く際の重要ポイント

散布図と相関係数は便利ですが、使い方を誤ると間違った結論を導いてしまいます。特に以下の3点には注意してください。

1. 相関関係は「因果関係」ではない

これは最も重要な注意点です。「勉強時間が多いほど、テストの点数が高い」（正の相関）というデータがあったとしても、それだけでは「勉強した"から"点数が上がった」とは断言できません。

もしかすると、「もともと地頭が良い人が、勉強もたくさんする傾向がある」だけかもしれませんし、第三の要因（例：塾に通っている）が両方に影響している可能性もあります。

>> 相関関係と因果関係の違いとは？データ分析で間違う前に知りたい基本

相関係数はあくまで「2つのデータが連動して動く傾向」を示すだけで、原因と結果の関係（因果関係）を証明するものではないことを肝に銘じておきましょう。

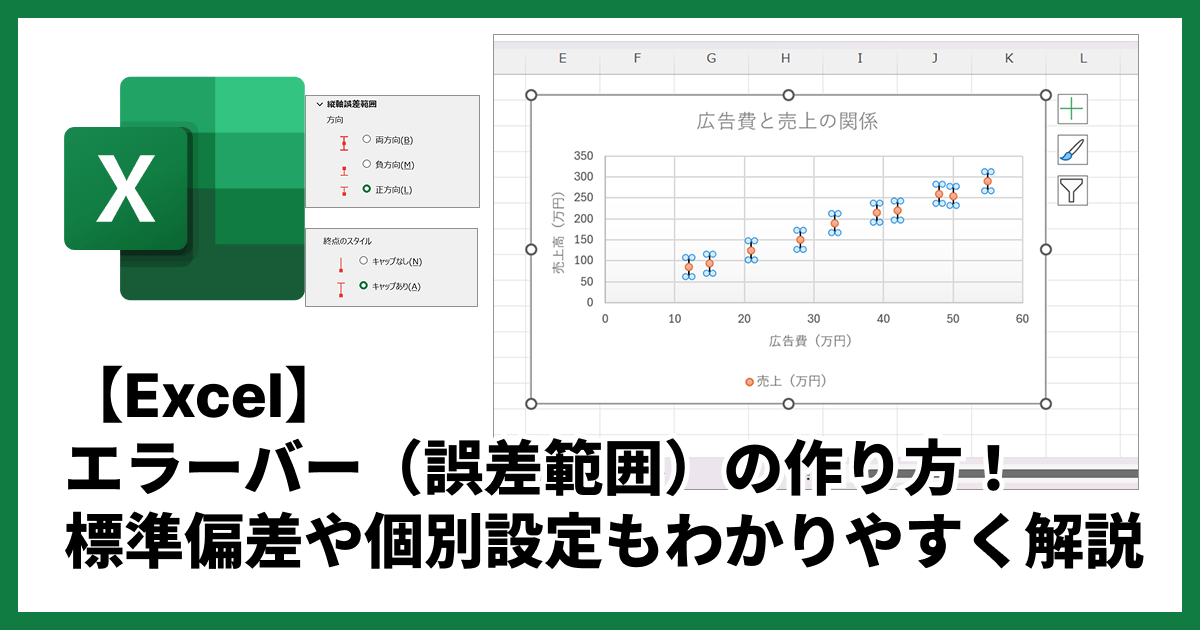
2. 「外れ値」に注意する

ほとんどのデータは無相関なのに、たった1点だけ極端に離れたデータ（外れ値）が存在すると、相関係数はそれに大きく引っ張られて、見かけ上高い値が出てしまうことがあります。
逆に、強い相関がありそうなのに、外れ値のせいで相関係数が低く出ることもあります。

だからこそ、相関係数の数値だけを見るのではなく、必ず散布図を描いて、データの分布や外れ値の有無を目で確認することが不可欠です。

3. 相関があるのは「直線的な関係」だけ

相関係数（特にピアソン）が捉えられるのは、「直線的な関係」だけです。

例えば、上図のようにU字型（二次関数的）な関係がある場合、2つのデータには明確な関係性がありますが、直線ではないため相関係数は0近くになってしまいます。散布図を見れば一目瞭然でも、数値だけでは見逃してしまうのです。

オンラインツールで簡単！散布図を作成してみよう

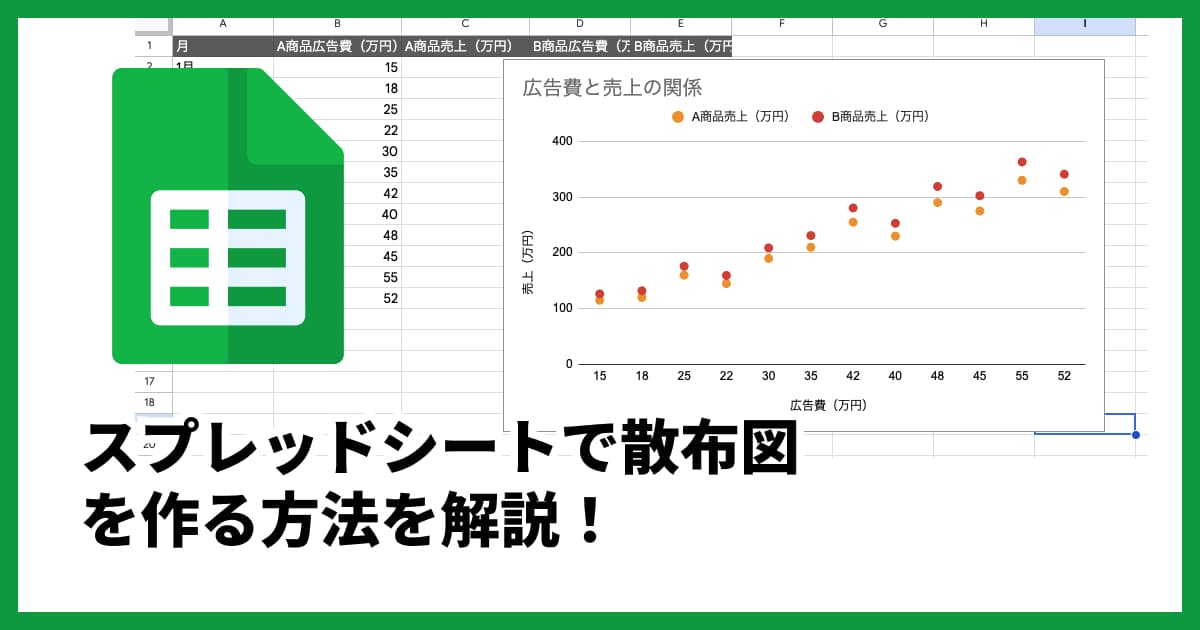
散布図と相関係数の関係性が理解できたら、次は実際に自分で作ってみましょう。ExcelやGoogleスプレッドシートでも散布図は作成できますが、もっと手軽に試したい方には、オンラインのグラフ作成ツールが便利です。

私たちが運営する「xGrapher」なら、会員登録不要・無料で、データをコピー＆ペーストするだけですぐに美しい散布図を作成でき相関係数も自動計算されます。

使い方は簡単です。

1. xGrapherの散布図作成ページにアクセスします。
   

   

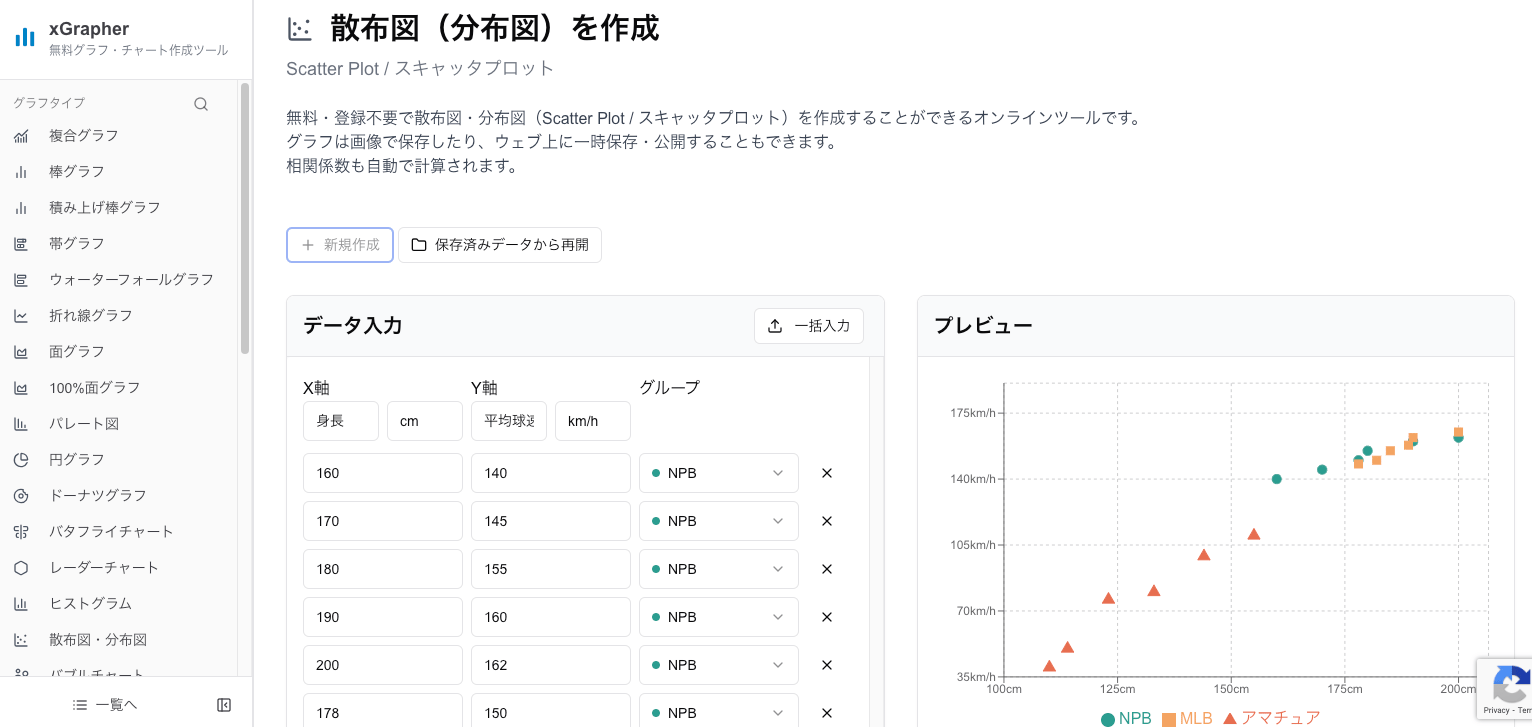
2. お手持ちのデータ（Excelやスプレッドシートの2列のデータなど）をコピーします。

3. xGrapherのデータ入力欄にペーストします。

4. 相関係数rは自動計算されオプションで表示・非表示を切り替えることができます
   

   

5. グラフのタイトルや軸ラベルを整えれば、すぐに散布図が完成します。

データ分析の第一歩として、まずは手軽にデータを可視化し、散布図のパターンを確認する習慣をつけましょう。

※Excelやスプレッドシートでの詳しい作成手順を知りたい方は、以下の記事も参考にしてください。

• Excel（エクセル）で散布図を作成する方法

• Googleスプレッドシートで散布図を作成する方法

まとめ：散布図と相関係数でデータ分析を深めよう

今回は、データ間の関係性を探るための基本ツールである「散布図」と「相関係数」について解説しました。

• 散布図: 2つのデータの関係性を視覚的に把握できるグラフ。

• 相関係数: 2つのデータの直線的な関係の「強さ」と「向き」を-1から1の数値で示す指標。

• ポイント: 相関係数の数値だけを鵜呑みにせず、必ず散布図とセットで確認する。

• 注意点: 「相関関係」は「因果関係」ではない。外れ値や非線形な関係にも注意する。

データ分析は、まずデータを「見てみる」ことから始まります。オンラインツールxGrapherなどを活用して、ぜひあなたのデータで散布図を作成し、隠れた関係性を探ってみてください。

関連記事:
決定係数 (R2) とは？相関係数 (r) との違いや散布図との関係性

散布図と相関係数に関するQ&A

Q1: 相関係数が0.5の場合、どう解釈すればよいですか？

A1: 一般的に「中程度の正の相関がある」と解釈されます。散布図にプロットすると、データはぼんやりと右肩上がりの傾向を示しているはずです。ただし、分野によってこの強さの解釈は異なる場合があります。

Q2: 相関係数が1.2になることはありますか？

A2: いいえ、ありません。相関係数（ピアソンの積率相関係数など）は、数学的に必ず-1から1の間の値をとります。もし計算結果が1を超えたり、-1を下回ったりした場合は、計算ミスや使用するデータの前提が間違っている可能性があります。

Q3: 相関係数がない散布図はありますか？

A3: 散布図は2つの量的データがあれば必ず作成できます。一方、相関係数は通常、2つの「量的変数」（数値データ）間の関係を測るために計算されます。「性別」と「点数」のような質的データと量的データの組み合わせでは、相関係数（ピアソン）は適切ではありません（他の分析手法を使います）。

Q4: 相関係数が高いほど、良いデータと言えますか？

A4: 一概には言えません。「相関が高い」とは、2つの変数の間に強い直線関係があることを示すだけです。それが分析の目的にとって「良い」かどうかは別問題です。また、Q5で触れる「偽りの相関」である可能性もあります。

Q5: 「偽りの相関（見せかけの相関）」とは何ですか？

A5: 2つのデータ間に直接的な因果関係がないにもかかわらず、あたかも相関があるかのように見える状態を指します。よくあるのは、「第三の因子」が両方のデータに影響しているケースです（例：「アイスの売上」と「水難事故件数」はどちらも「気温」という第三の因子によって増えるため、正の相関を示しますが、アイスが事故の原因ではありません）。相関関係と因果関係を混同しないためにも重要な概念です。
>> 偽相関（見せかけの相関）とは？データに騙されないための具体例と見抜き方