相関関係と因果関係の違いとは？データ分析で間違う前に知りたい基本【具体例で解説】

相関関係とは？ ～2つの変数の「連動」～

相関関係とは、簡単に言うと「2つの事柄（変数）が、一方が増えるともう一方も増える（または減る）といったように、連動して動く関係」のことです。

あくまで「連動している」という状態を示しているだけで、どちらかが原因で、どちらかが結果であるかは問いません。

相関関係には、主に3つのパターンがあります。

• 正の相関: 一方が増える（減る）と、もう一方も増える（減る）関係。

  • 例：身長と体重、勉強時間とテストの点数

• 負の相関: 一方が増える（減る）と、もう一方は減る（増える）関係。

  • 例：気温と暖房器具の売上、運動量と体脂肪率

• 無相関: 2つの事柄に関連性が見られない状態。

  • 例：今日の株価とあなたのランチのメニュー

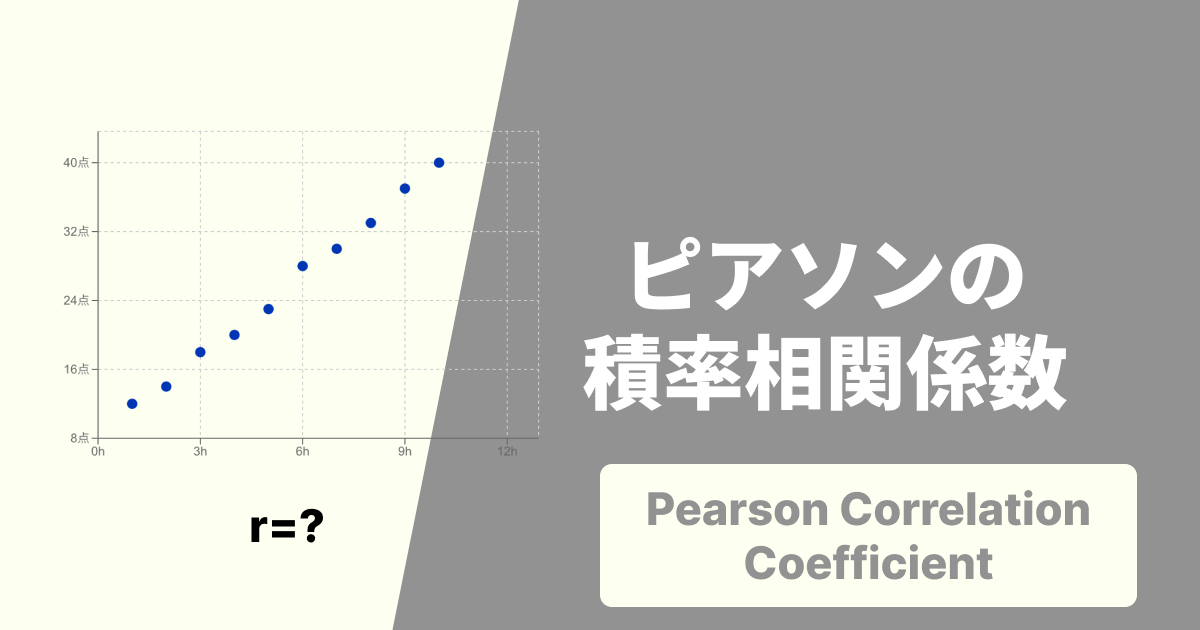
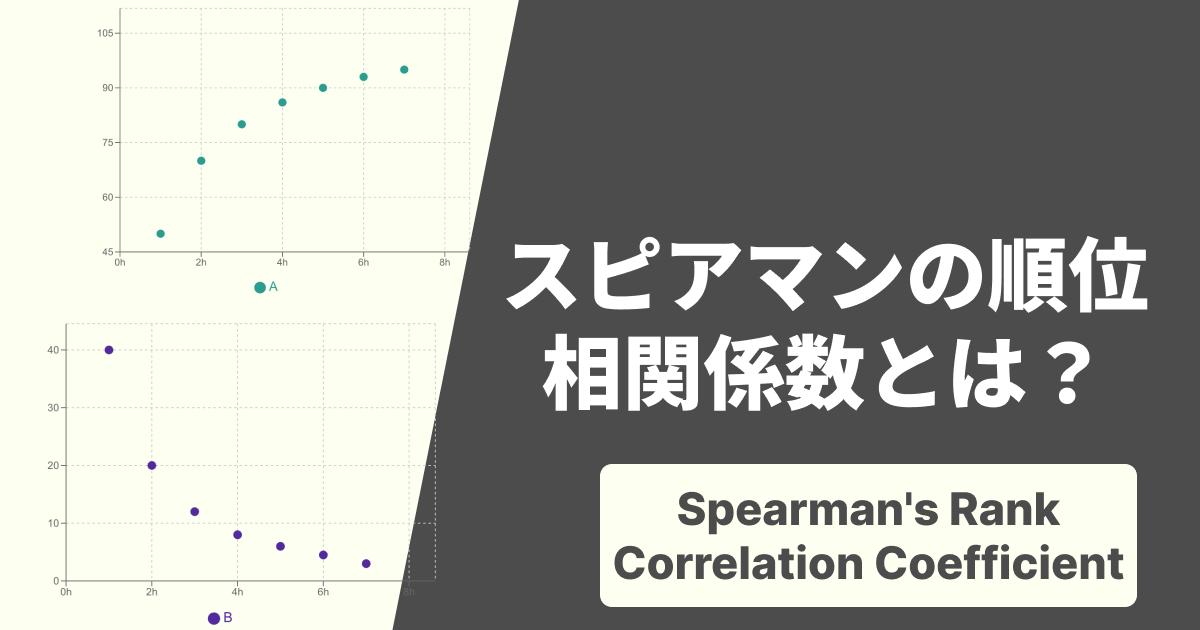
このような相関関係の強さや向きは、散布図を作成してみると視覚的に分かりやすく把握できます。また、「相関係数」という指標（-1から1までの値）で数値的に表すことも可能です。

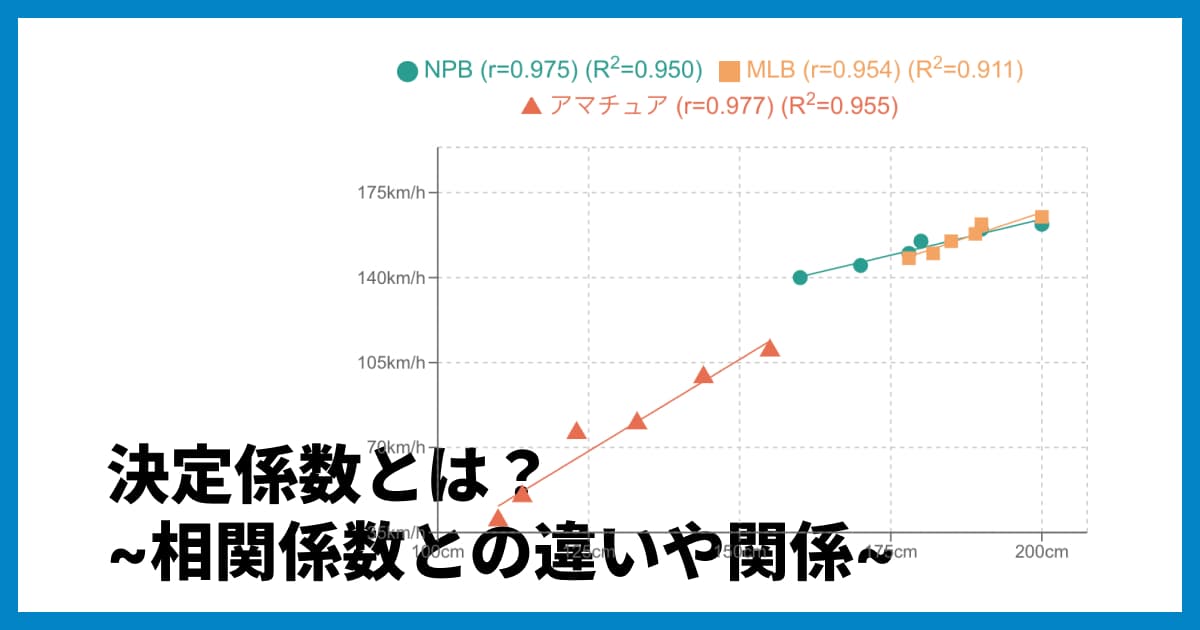
※相関係数について詳しく知りたい方は、こちらの記事「相関係数rの求め方とエクセルでの計算方法」も参考にしてみてください。

因果関係とは？ ～明確な「原因と結果」～

因果関係とは、「一方の事柄（原因）が、もう一方の事柄（結果）を引き起こしている関係」のことです。

ここには明確な「原因→結果」という一方通行の流れが存在します。

• 例1：「（原因）ボタンを押す」→「（結果）電源が入る」

• 例2：「（原因）ウイルスに感染する」→「（結果）熱が出る」

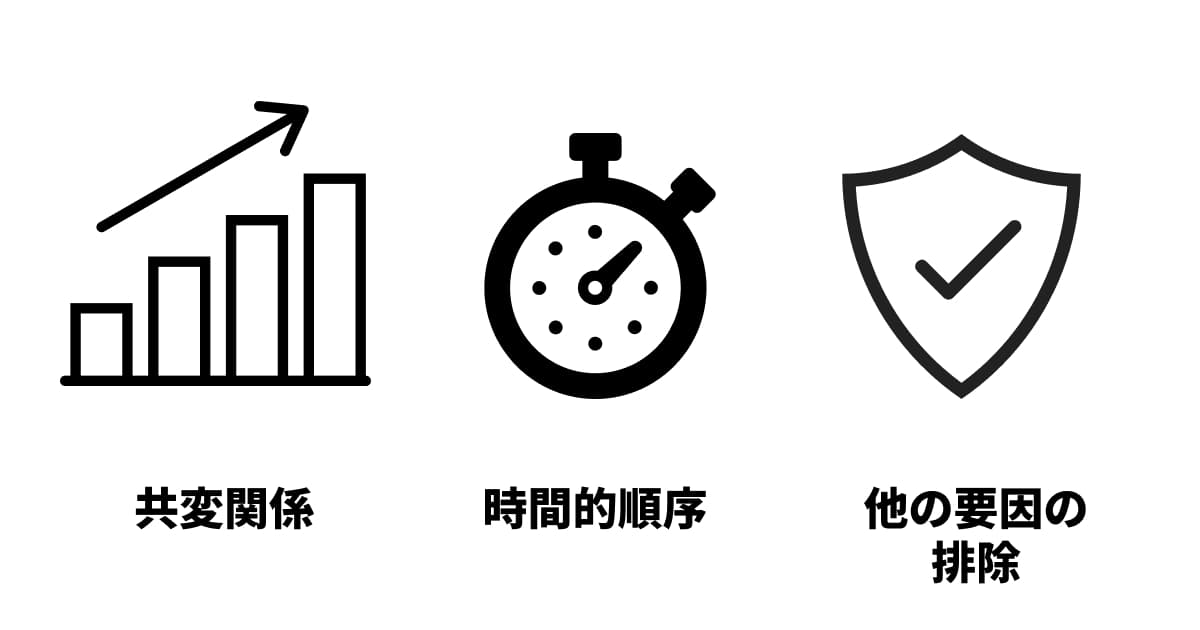
因果関係が成立するためには、一般的に以下の3つの条件が必要とされます。

1. 共変関係: 原因と結果が連動している（相関関係がある）。

2. 時間的順序: 原因が結果よりも先に発生している。

3. 他の要因の排除: 他の要因が結果を引き起こしている可能性がない（＝その原因だけが結果に影響していると特定できる）。

決定的な違いと「相関≠因果」の理由

ここまで見てきたように、相関関係と因果関係の決定的な違いは、「そこに原因と結果の関係が明確にあるかどうか」です。

• 相関関係: 2つの変数が「連動」している状態。（原因と結果は問わない）

• 因果関係: 一方が「原因」で、もう一方が「結果」である状態。

ここで最も重要なルールは、
「相関関係があるからといって、必ずしも因果関係があるとは限らない」（相関≠因果）
ということです。

一方で、「因果関係がある」場合、その2つの変数間には（何らかの）「相関関係が見られる」ことがほとんどです。（例：勉強時間を増やす「原因」→点数が上がる「結果」。これには正の相関があります）

しかし、逆は成り立ちません。「連動している」ように見える2つの事柄が、実はまったくの偶然だったり、次に説明する「見せかけの相関」だったりすることが非常に多いためです。

>> 擬似相関・見せかけの相関についての解説記事

なぜ間違えやすい？「擬似相関（見せかけの相関）」のワナ

「相関≠因果」を理解する上で、最も有名なワナが「擬似相関（ぎじそうかん）」です。

擬似相関とは、2つの事柄（AとB）に相関関係が見られるものの、実際にはAとBの間に直接的な因果関係はなく、別の要因（C）がAとBの両方に影響を与えている状態を指します。このCを「交絡因子（こうらくいんし）」や「潜在変数」と呼びます。

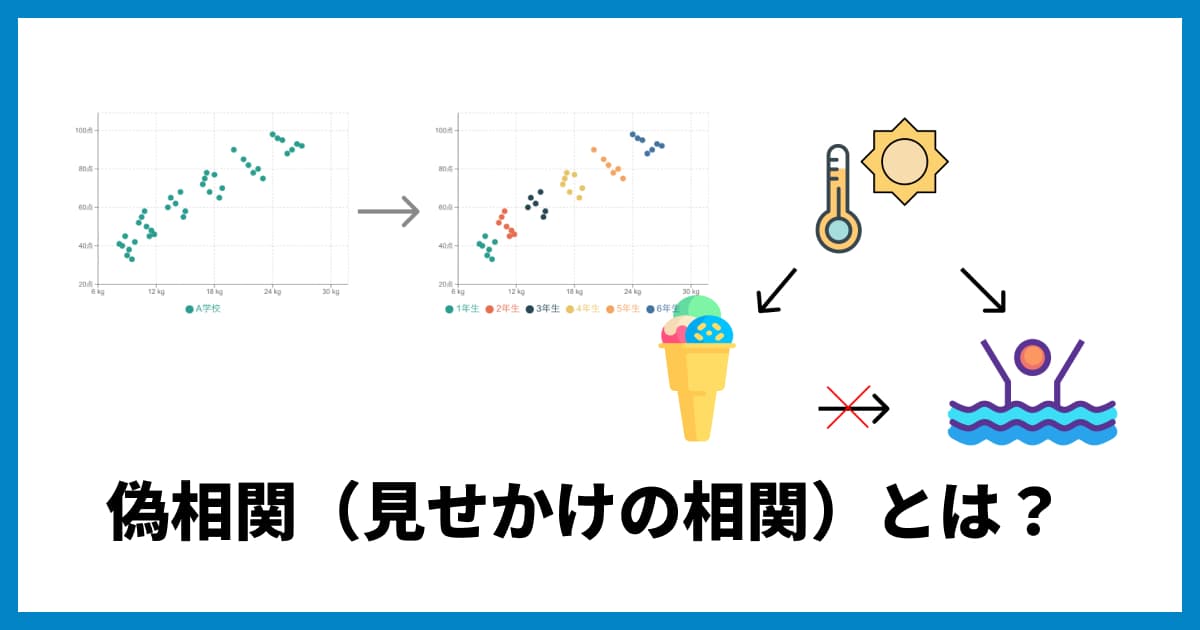
【超有名】擬似相関の例：アイスの売上と水難事故

データを見ると、「アイスクリームの売上が増える（A）」と「水難事故の件数が増える（B）」の間には、強い正の相関が見られます。

もしここで「相関＝因果」と勘違いし、「アイスの売上が増えると水難事故が増えるんだ！だから水難事故を防ぐためにアイスの販売を禁止しよう！」と結論づけてしまったらどうでしょうか？
これは明らかに間違っていますよね。

この場合の「隠れた要因（交絡因子C）」は「気温（暑さ）」です。

• （C）気温が上がる → （A）アイスが売れる

• （C）気温が上がる → （B）海や川で泳ぐ人が増え、水難事故が増える

このように、AとBはどちらも「気温」という共通の原因によって引き起こされた「結果」であり、AとBの間に直接的な因果関係はありません。これこそが擬似相関です。

※擬似相関については、こちらの記事「擬似相関とは？相関関係と因果関係を混同しないための具体例」でさらに多くの例を紹介しています。

>> 面白い擬似相関の例 | ニコラス・ケイジ出演で溺死者増？

ビジネスやデータ分析で間違えるとどうなる？

この「相関≠因果」の勘違いは、ビジネスの現場でも深刻な問題を引き起こす可能性があります。

例：広告費と売上
「広告費（A）を増やした月」と「売上（B）が増えた月」に正の相関が見られたとします。

ここで「広告費を増やしたから（原因）、売上が増えた（結果）のだ」と安易に因果関係を結論づけてしまうのは危険です。

もしかすると、

• （交絡因子C）たまたまその月がボーナス商戦期だったから、広告を出さなくても売上は増えたかもしれない。

• （交絡因子C）競合他社が値下げをしたから、慌てて広告費を増やし、結果的に売上も（競合から流れてきて）増えただけかもしれない。

• （逆の因果）売上が好調だったから（原因）、余った予算で広告費を増やした（結果）だけかもしれない。

もし擬似相関である可能性を検証せず、「広告費が原因だ！」と信じて広告費を使い続けても、期待した売上アップにはつながらないかもしれません。

本当に「広告Aが原因で売上が上がったのか」を確かめるには、A/Bテストのような、他の条件を揃えて比較する実験（因果推論の手法）が必要になります。

相関関係を視覚化してみよう

データ分析の第一歩は、「本当にそこに関係があるのか？」を疑うことから始まります。そして、関係性を大まかに把握するために最も役立つのが「散布図」です。

散布図は、2つの変数をX軸とY軸にとり、データを点でプロットしたグラフです。点の集まりが右上がりなら「正の相関」、右下がりなら「負の相関」、バラバラなら「無相関」と、一目で関係性を把握できます。

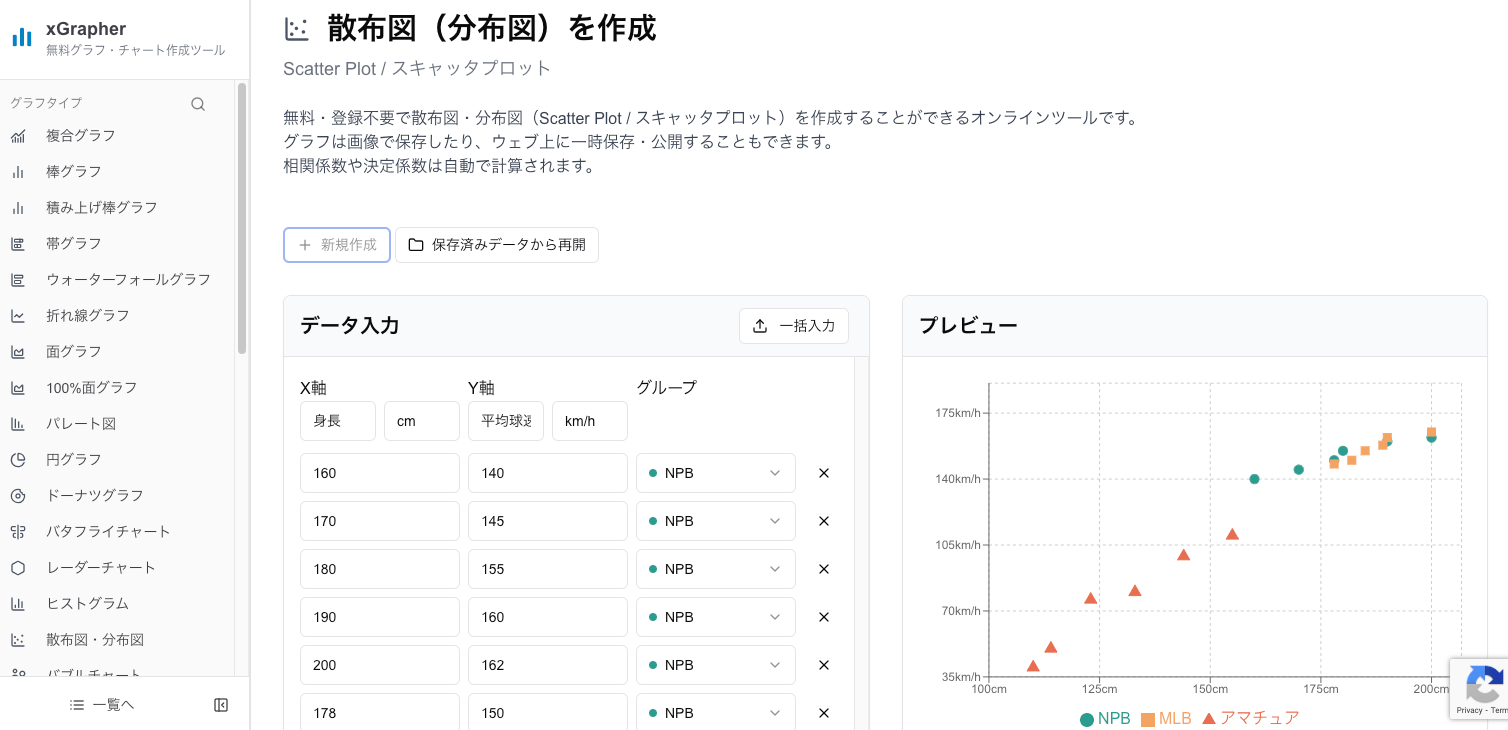
オンライングラフ作成ツールの xGrapher を使えば、Excelやスプレッドシートがなくても、Webブラウザ上で簡単にきれいな散布図を作成できます。
「このデータとあのデータ、関係あるかも？」と思ったら、まずはデータをコピー＆ペーストして散布図を作ってみましょう。関係性が見えてくるかもしれません。

➡️ xGrapherで散布図を無料で作成する

（散布図の見方や作り方については、散布図とは？見方や書き方、相関関係の読み取り方を解説 や 相関関係がわかるグラフとは？散布図と相関係数について解説 もご参照ください。）

まとめ：データに騙されないために

今回は、「相関関係」と「因果関係」の違いについて解説しました。

• 相関関係: 2つの変数が「連動」している状態。

• 因果関係: 一方が「原因」で、もう一方が「結果」である状態。

• 最重要ルール: 「相関関係があっても、因果関係があるとは限らない（相関≠因果）」

• 注意点: 擬似相関（共通の原因CがAとBの両方を動かしている）に注意する。

データを見て「関係がありそうだ（相関）」と感じたときは、すぐに「これが原因だ（因果）」と飛びつかず、「本当にそうか？」「他に隠れた要因（交絡因子）はないか？」「逆の因果関係ではないか？」と一歩立ち止まって考えるクセをつけることが、データに騙されないための最も重要なスキルです。

よくある質問 (Q&A)

Q1. 「相関関係」と「因果関係」は、どちらが先に見つかりますか？
A1. 一般的には「相関関係」が先に観測されます。データを見て「あれ、この2つは連動しているな（相関）」と気づくことがスタートです。その上で、「もしかして、こちらが原因でこちらが結果なのでは？（因果）」という仮説を立て、A/Bテストなどで検証していく、という流れが一般的です。

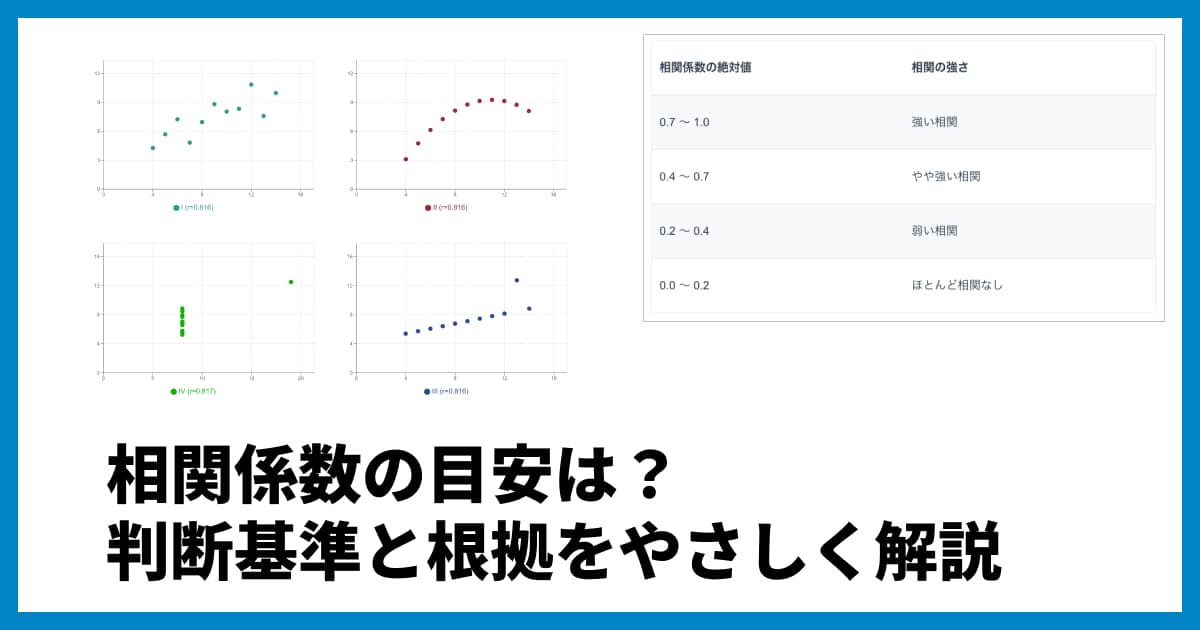
Q2. 相関係数が高ければ（1や-1に近ければ）、因果関係も強いと言えますか？
A2. いいえ、言えません。相関係数はあくまで「相関の強さ（連動の度合い）」を示す数値です。Q5で紹介する「擬似相関」の例でも、非常に高い相関係数が出ることはありますが、そこに因果関係はありません。「相関の強さ」と「因果関係の有無」は別問題として考える必要があります。
>> 相関係数の目安とその根拠の解説記事

Q3. 因果関係があるのに、相関関係が見られないことはありますか？
A3. まれにありますが、少し複雑なケースです。例えば、U字型（または逆U字型）の関係（例：ストレスが少なすぎても多すぎてもパフォーマンスが下がり、適度なストレスが最もパフォーマンスが高い）の場合、全体で見ると「無相関」のように見えることがあります。また、他の要因が強く影響して、本来あるはずの因果関係が見えにくくなることもあります。

Q4. 因果関係を証明するにはどうすればいいですか？
A4. 厳密に因果関係を証明するのは非常に難しいですが、最も強力な方法とされるのが「ランダム化比較試験（RCT）」です。これは、対象者をランダムに2つのグループに分け、一方にだけ（原因となる）施策を行い、もう一方（何もしない）と比較して結果に差が出るかを見る方法です。Webマーケティングでの「A/Bテスト」もこれに近いです。

Q5. 擬似相関の面白い例は他にありますか？
A5. 有名なものに「消防車の出動台数と火災の被害額（どちらも「火事の規模」という交絡因子による）」「チョコレートの消費量が多い国とノーベル賞受賞者数（どちらも「国の経済的豊かさ」などが関係している可能性）」などがあります。これらは明らかに因果関係がないと分かりやすいため、擬似相関の例としてよく使われます。
参考記事: 擬似相関とは？相関関係と因果関係を混同しないための具体例