ケンドールの順位相関係数（τ）とは？計算方法や意味をわかりやすく解説

なぜ順位相関？ピアソンの相関係数との違い

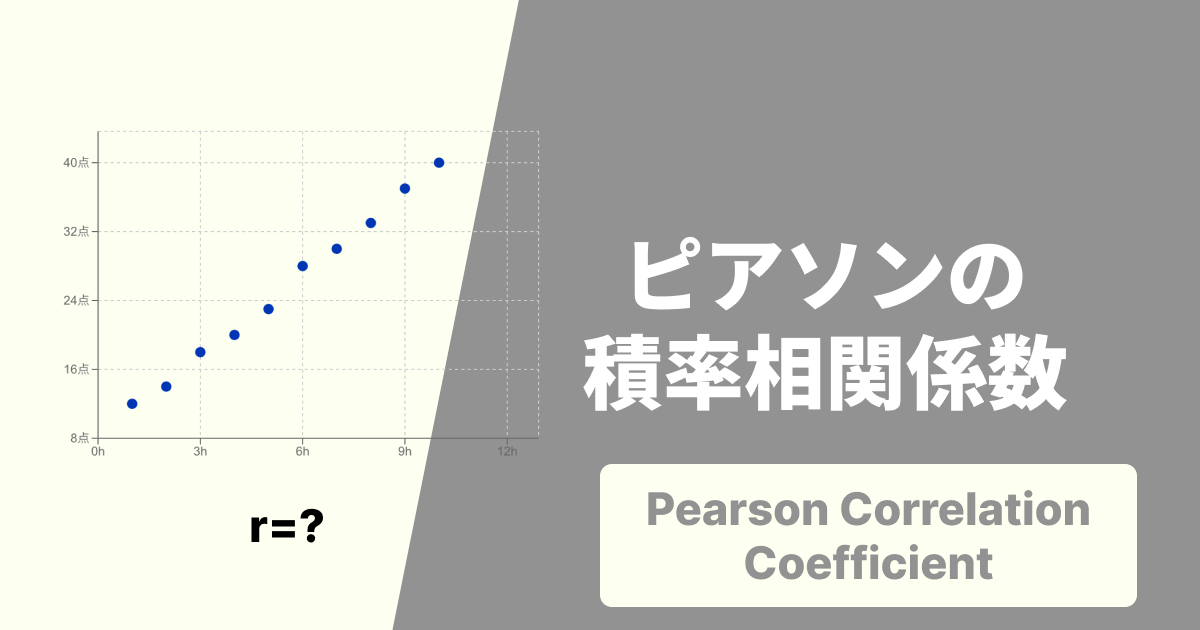
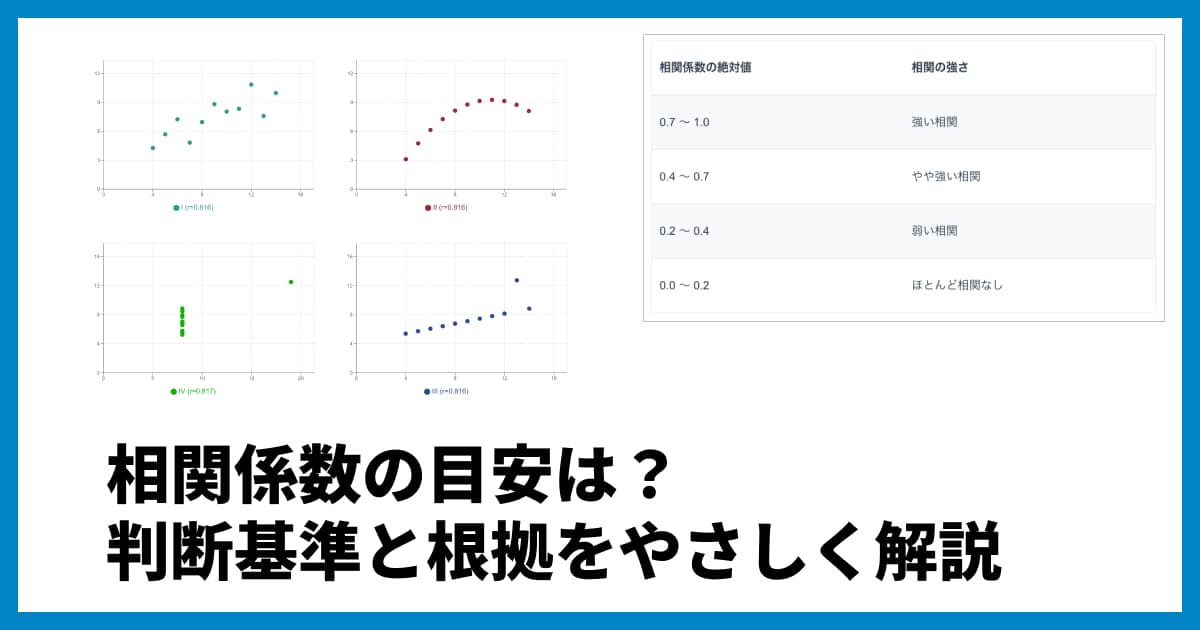
「相関係数」と聞くと、多くの人がピアソンの積率相関係数（$r$）を思い浮かべるかもしれません。ピアソンの相関係数は、2つの変数がどれだけ直線的な関係にあるかを $-1$ から $+1$ の値で示します。

しかし、データによってはピアソンの相関係数が適さない場合があります。

• データが「順序尺度」の場合:
  「満足度（5:とても満足 〜 1:とても不満）」や「成績（A, B, C, D）」のように、大小関係や順序には意味があるものの、その間隔が一定でないデータ（順序尺度）には、ピアソンの相関係数は使えません。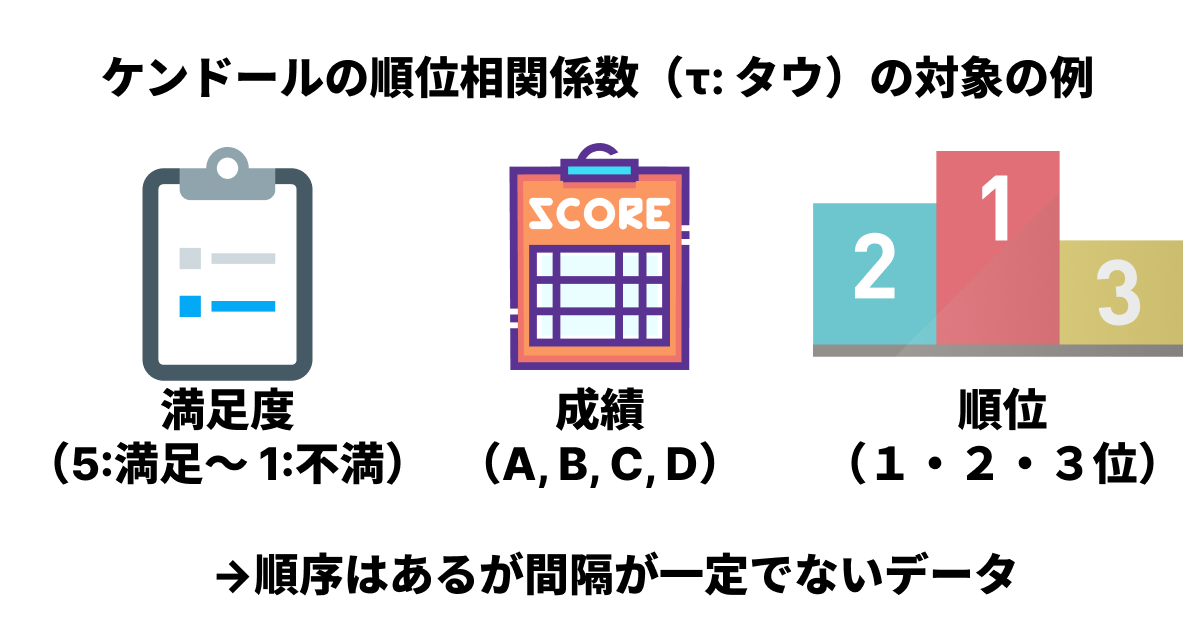
  

  

• 外れ値に弱い:
  ピアソンの相関係数は、平均値からのズレ（偏差）を使って計算するため、一つだけ極端にかけ離れた値（外れ値）があると、その値に引っ張られて相関が正しく評価できないことがあります。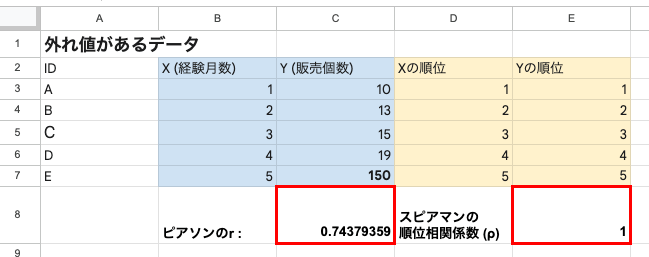
  

  

• 直線的ではない「単調な関係」を見たい場合:
  「片方が増えれば、もう片方も（一貫して）増える（または減る）」という単調な関係（単調増加・単調減少）を見たい場合、ピアソンの相関係数は関係性を過小評価することがあります。

このような場合に活躍するのが「順位相関係数」です。順位相関係数は、実際の値ではなく、データを小さい（または大きい）順に並べ替えた「順位」を使って計算します。そのため、外れ値の影響を受けにくく、順序尺度データにも使え、単調な関係性を評価するのに適しています。

ケンドールの順位相関係数とスピアマンの順位相関係数は、この順位相関係数の代表的な2つの手法です。

ケンドール（τ）とスピアマン（ρ）の主な違い

どちらも順位を使って計算する点は同じですが、計算のアプローチと考え方が異なります。

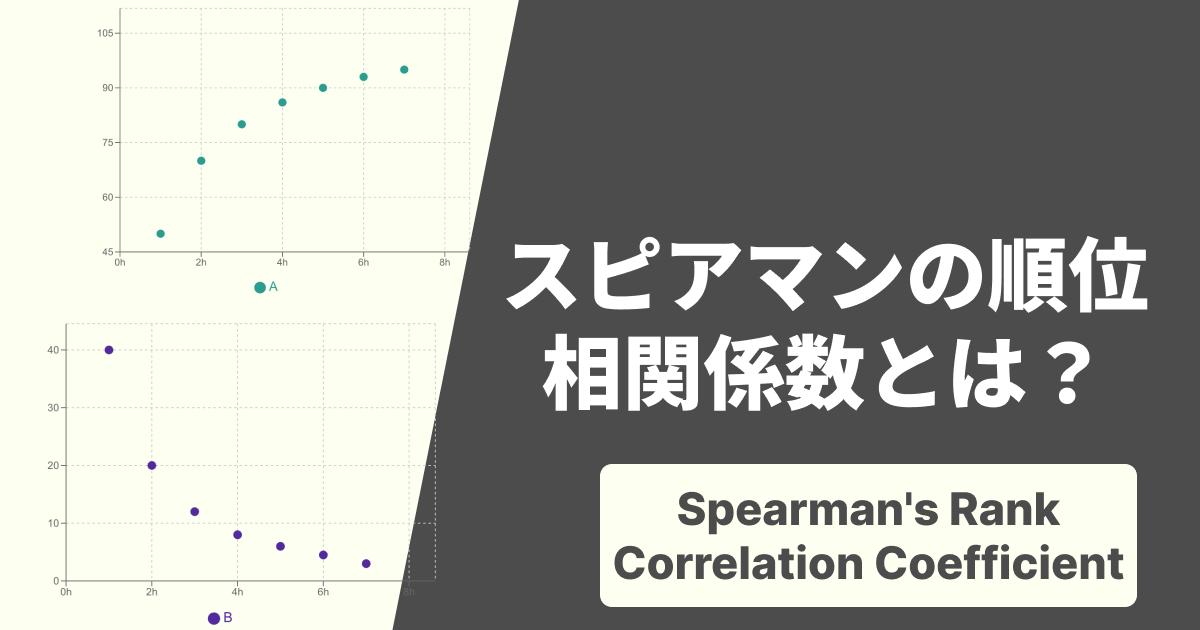
スピアマンの順位相関係数（$\rho$）は、ピアソンの積率相関係数の計算式に、実際の値の代わりに「順位」を当てはめて計算したものです。順位の「ズレ」がどれくらいかを評価します。

一方、ケンドールの順位相関係数（$\tau$）は、全く異なるアプローチを取ります。
データの中から2つのペアを取り出し、「Aさんの順位（X, Y）とBさんの順位（X, Y）を比べたとき、両方ともAさんの方が上か？（または両方ともBさんの方が上か？）」という順序の一致度を見ていきます。

どちらを使うべきか迷うかもしれませんが、スピアマンの方が計算が簡単なため広く使われる傾向にありますが、ケンドールの方がデータの「順序の一致性」をより直接的に評価しており、特にタイ（同順位）が多いデータに強いとされています。

>> スピアマンの順位相関係数とは？ピアソンとの違いなどわかりやすく解説

ケンドールの順位相関係数τ の計算方法

ケンドールの $\tau$ は、データのすべてのペア（組み合わせ）を調べ、「一致ペア（Concordant Pair）」と「不一致ペア（Discordant Pair）」の数を数えることから始まります。

データが $n$ 個ある場合、ペアの総数は ${}_n C_2 = \frac{n(n-1)}{2}$ 通りです。

ある2つのデータペア $(x_i, y_i)$ と $(x_j, y_j)$ に注目します。

• 一致ペア (C):
  $x_i < x_j$ かつ $y_i < y_j$ （両方とも $i$ より $j$ が大きい）
  または
  $x_i > x_j$ かつ $y_i > y_j$ （両方とも $i$ より $j$ が小さい）
  ...つまり、Xの順序とYの順序が一致しているペア。

• 不一致ペア (D):
  $x_i < x_j$ かつ $y_i > y_j$ （Xは $j$ が大きいが、Yは $i$ が大きい）
  または
  $x_i > x_j$ かつ $y_i < y_j$ （Xは $i$ が大きいが、Yは $j$ が大きい）
  ...つまり、Xの順序とYの順序が逆転しているペア。

（※タイ（同順位）がない場合を想定しています。タイについては後述します）

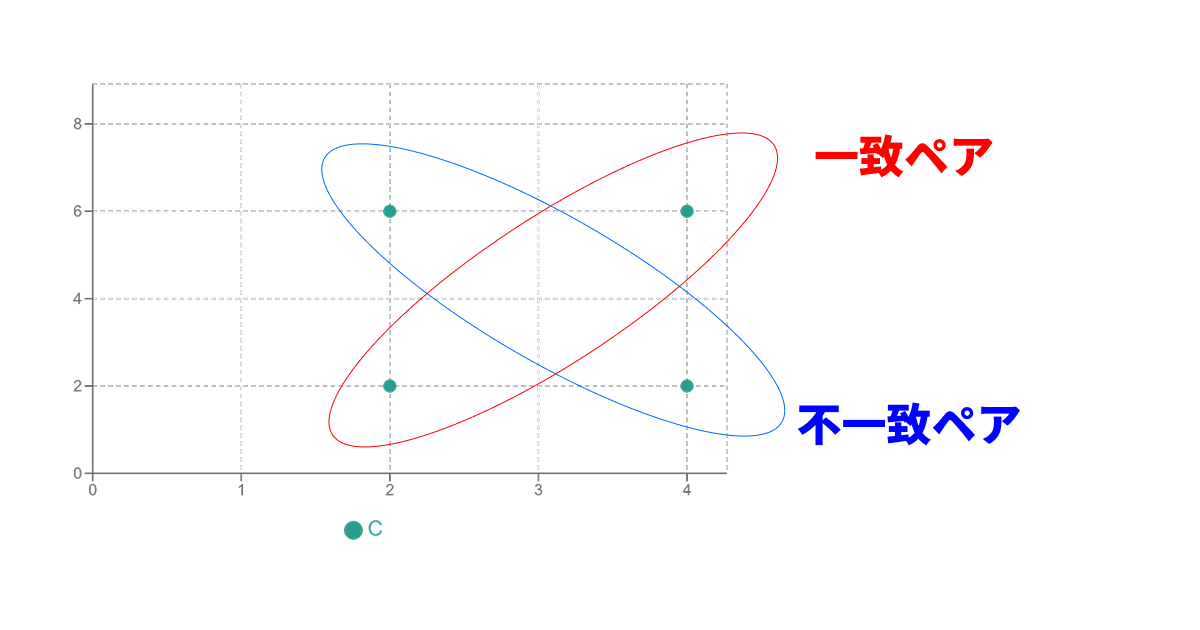
一致ペアの数を $C$、不一致ペアの数を $D$ とすると、ケンドールの順位相関係数（$\tau_a$：タウ・エーと呼ばれ、タイがない場合に使う）は以下の式で計算されます。
$\tau_a = \frac{C - D}{C + D} = \frac{C - D}{\frac{n(n-1)}{2}}$

• すべてのペアが一致ペア（完全な正の相関）なら $D=0$ となり、$\tau_a = \frac{C}{C} = 1$ です。

• すべてのペアが不一致ペア（完全な負の相関）なら $C=0$ となり、$\tau_a = \frac{-D}{D} = -1$ です。

• 一致ペアと不一致ペアの数が同じなら $C=D$ となり、$\tau_a = \frac{0}{C+D} = 0$ （無相関）です。

具体例で計算してみよう（タイがない場合）

5人の生徒の「数学の順位(X)」と「理科の順位(Y)」のデータで計算してみます。

まず、計算しやすいようにXの順位（数学）で並べ替えます（この例では既に並んでいます）。
次に、AさんからEさんまで、自分より下の行のデータとペアを作っていき、Y（理科）の順位を比較します。

ペアの総数は ${}_5 C_2 = \frac{5 \times 4}{2} = 10$ 通りです。

1. A (1, 2) とのペア:

   • vs B (2, 1): Xは $1<2$, Yは $2>1$ → 不一致 (D)

   • vs C (3, 4): Xは $1<3$, Yは $2<4$ → 一致 (C)

   • vs D (4, 3): Xは $1<4$, Yは $2<3$ → 一致 (C)

   • vs E (5, 5): Xは $1<5$, Yは $2<5$ → 一致 (C)

2. B (2, 1) とのペア:

   • vs C (3, 4): Xは $2<3$, Yは $1<4$ → 一致 (C)

   • vs D (4, 3): Xは $2<4$, Yは $1<3$ → 一致 (C)

   • vs E (5, 5): Xは $2<5$, Yは $1<5$ → 一致 (C)

3. C (3, 4) とのペア:

   • vs D (4, 3): Xは $3<4$, Yは $4>3$ → 不一致 (D)

   • vs E (5, 5): Xは $3<5$, Yは $4<5$ → 一致 (C)

4. D (4, 3) とのペア:

   • vs E (5, 5): Xは $4<5$, Yは $3<5$ → 一致 (C)

結果を集計します。

• 一致ペア (C) = 8

• 不一致ペア (D) = 2

$\tau_a$ を計算します。

ケンドールの順位相関係数は 0.6 となり、「中程度の正の相関」があることがわかりました。

タイ（同順位）がある場合の計算方法: ケンドールのτb（タウ・ビー）

実際のデータでは、同順位（タイ）が発生することがよくあります。
例えば、「数学の順位が2位の人が2人いる」といったケースです。

タイがある場合、先ほどの $\tau_a$ の計算式（分母が $C+D$）では、タイになったペアが分母から除外されてしまうため、相関係数が理論上の最大値（1）や最小値（-1）に届かなくなってしまいます。

そこで、タイを考慮したケンドールの $\tau_b$（タウ・ビー）が用いられます。

計算は複雑になりますが、考え方は「Xだけにタイがあるペアの数（$T_x$）」と「Yだけにタイがあるペアの数（$T_y$）」もカウントし、分母を補正します。

ペアの総数 $N = \frac{n(n-1)}{2}$ は、以下のように分解されます。
$N = C + D + T_x + T_y + T_{xy}$ （$T_{xy}$ はXもYもタイのペア。$\tau_b$ では使わない）

$\tau_b$ の計算式は以下の通りです。

または、タイの補正項を $T_x = \sum \frac{t_i(t_i-1)}{2}$ （$t_i$ はXの各タイグループの人数）、$T_y = \sum \frac{u_j(u_j-1)}{2}$ （$u_j$ はYの各タイグループの人数）として、以下の式で計算することも一般的です。

手計算は非常に手間がかかるため、通常は統計ソフトやExcelの関数（アドインが必要な場合あり）、Pythonなどのプログラミング言語、あるいは専用のツールを使って計算します。

相関関係を視覚的に捉えるヒント

ケンドールの $\tau$ もスピアマンの $\rho$ も、相関関係を見るための指標ですが、計算が複雑で、特にデータ数が増えると手計算は現実的ではありません。

相関を分析する第一歩として、まずはデータを散布図にして視覚的に確認することが非常に重要です。

散布図にすることで、

• 全体的に右肩上がり（正の相関）か、右肩下がり（負の相関）か

• 関係性は直線的か、曲線的（単調増加など）か

• 外れ値がないか

といったデータの傾向を一目で把握できます。

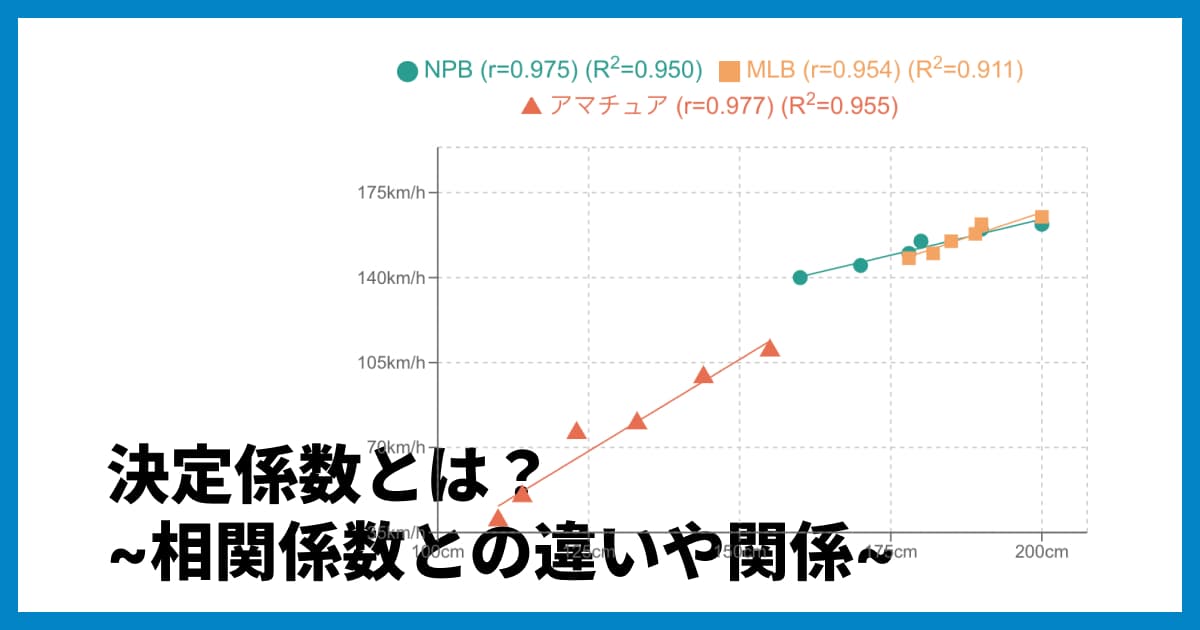
オンライングラフ作成ツールの xGrapher では、CSVやExcel、スプレッドシートのデータをコピー＆ペーストするだけで、簡単に高機能な散布図を作成できます。

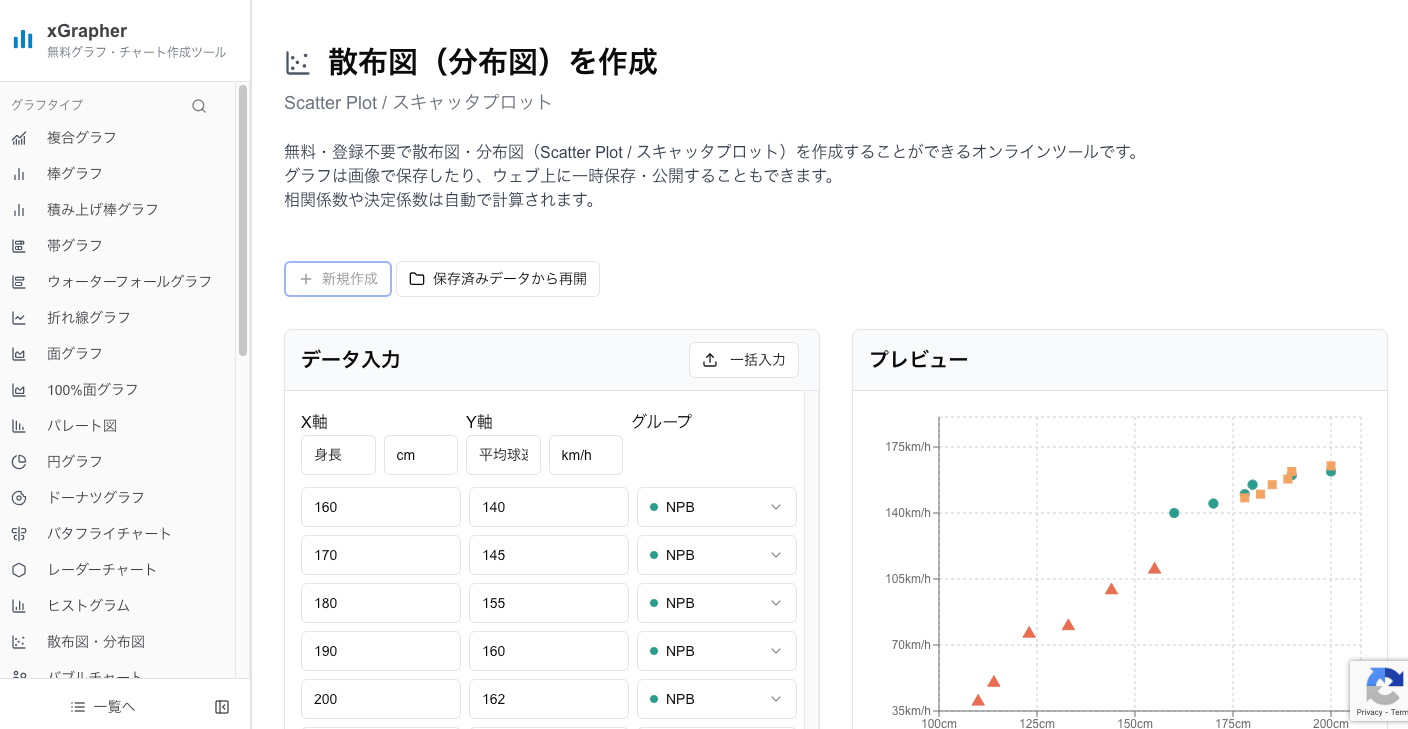
xGrapherは無料で利用でき、ピアソンの相関係数 Rや決定係数R2は自動計算されます。

順位相関を計算する前に、まずxGrapherで散布図を作成し、「そもそも順位で相関を見るべきデータなのか」を視覚的に判断する習慣をつけると、より適切なデータ分析ができるようになるでしょう。

まとめ

今回は、順位どうしの関連性を見る「ケンドールの順位相関係数（$\tau$）」について解説しました。

• ケンドールの $\tau$ は、順序尺度データや外れ値があるデータ、単調な関係を見たい場合に使う順位相関係数の一つです。

• 「一致ペア（順序が同じ）」と「不一致ペア（順序が逆）」の数に基づいて計算されます。

• スピアマンの $\rho$ と比べ、計算は複雑ですが、タイ（同順位）に強いという特徴があります。

• 手計算は大変なため、まずは散布図などでデータの傾向を視覚的に掴むことが大切です。

どの相関係数を使うかは、データの種類や見たい関係性によって決まります。それぞれの特徴を理解し、適切に使い分けましょう。

関連記事:
Excelでの散布図作成
Googleスプレッドシートでの散布図作成

ケンドールの順位相関係数に関するQ&A

Q1: ケンドールの $\tau$ とスピアマンの $\rho$ は、どちらを使えば良いですか？
A1: どちらも順位に基づく相関を見る優れた指標ですが、特徴が異なります。データ数が多く計算負荷を抑えたい場合や、順位の「差」を重視したい場合はスピアマン（$\rho$）が選ばれることが多いです。一方、同順位（タイ）が多いデータや、ペアごとの「順序の一致性」を厳密に評価したい場合はケンドール（$\tau$）が適しているとされます。

Q2: ケンドールの $\tau$ の値は、どう解釈すれば良いですか？
A2: ピアソンの相関係数と同様に、$-1$ から $+1$ までの値をとり、以下のように解釈するのが一般的です。

• $+1$ に近い: 強い正の順位相関（片方の順位が上がれば、もう片方の順位も上がる傾向が強い）

• $-1$ に近い: 強い負の順位相関（片方の順位が上がれば、もう片方の順位は下がる傾向が強い）

• 0に近い: 順位相関はほとんどない
  一般的に、絶対値が 0.7 以上なら「強い相関」、0.4〜0.7 なら「中程度の相関」、0.2〜0.4 なら「弱い相関」、0.2 未満なら「ほとんど相関なし」とされますが、これは分野によって目安が異なります。

>> 相関係数の目安やその根拠についての解説

Q3: $\tau_a$, $\tau_b$, $\tau_c$ の違いは何ですか？
A3: これらはすべてケンドールの順位相関係数ですが、主にタイ（同順位）の扱いで区別されます。

• $\tau_a$ (タウ・エー): タイが全くないデータ用です。分母は単純にペアの総数 ($C+D$) です。

• $\tau_b$ (タウ・ビー): タイを考慮した最も一般的な指標です。XのタイとYのタイの両方を考慮して分母を補正します。正方行列（Xのカテゴリ数とYのカテゴリ数が同じ）のデータに適しています。

• $\tau_c$ (タウ・シー): $\tau_b$ と同様にタイを考慮しますが、非正方行列（XとYのカテゴリ数が異なる）のデータ（クロス集計表など）に適した補正を行います。

Q4: ケンドールの $\tau$ は外れ値に強いというのは本当ですか？
A4: はい、強いです。ピアソンの相関係数は「値そのもの」を使うため、極端に大きな値や小さな値（外れ値）があると、平均値が引っ張られ、相関係数の値が大きく歪んでしまいます。一方、ケンドールの $\tau$ は「順位」しか見ません。例えば、1位の値が100でも10000でも「1位」として扱われるため、外れ値の影響を非常に受けにくいという利点があります。

Q5: Excelでケンドールの $\tau$ を計算できますか？
A5: Excelの標準関数には、ケンドールの $\tau$ を直接計算するものはありません（ピアソン CORREL やスピアマン CORREL(RANK(X), RANK(Y)) とは異なります）。分析ツールアドインを追加したり、複雑な式を組んだり、VBA（マクロ）を使ったりすれば可能ですが、手軽ではありません。統計解析ソフトやPythonライブラリ（scipy.stats.kendalltau）などを使うのが一般的です。まずは散布図で傾向を見ることから始めるのが良いでしょう。