スピアマンの順位相関係数とは？ピアソンとの違いなどわかりやすく解説

スピアマンの順位相関係数を使う場面は？ピアソンとの違い

スピアマンの順位相関係数がいつ役立つのか、最も一般的なピアソンの積率相関係数との違いから見ていきましょう。

違い①：データの種類（順序尺度データでも使える）

ピアソンの相関係数は、基本的に「間隔尺度」や「比例尺度」（例：身長、体重、温度、点数など）のデータを対象とし、データが正規分布に従うこと（パラメトリック）を前提としています。

一方、スピアマンの順位相関係数は、データを順位に変換して扱うため、以下のようなデータでも使用できます。

• 順序尺度データ: 「満足度（5:とても満足 〜 1:とても不満）」「成績（A, B, C, D）」「好き嫌いの順位」など、順序はあるが間隔が一定でないデータ。

• 正規分布していないデータ: ピアソンの前提が満たせない、分布に偏りがあるデータ。

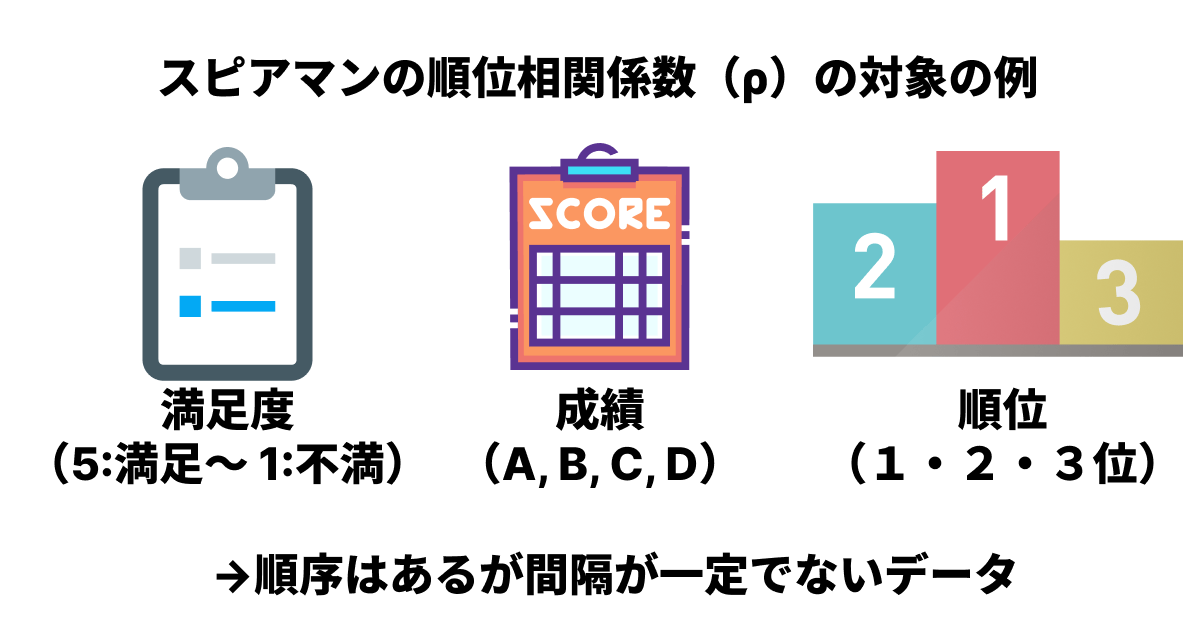
このように、スピアマンはピアソンよりも広い範囲のデータに使えるため、ノンパラメトリックな手法と呼ばれます。

違い②：関係性の捉え方（「線形関係」ではなく「単調関係」）

これが最も重要な違いです。

• ピアソン: 2つの変数が「線形関係」（一方が増えると、もう一方も直線的に増える/減る）にあるかを測定します。

• スピアマン: 2つの変数が「単調関係」（一方が増えると、もう一方も傾向として増える/減る）にあるかを測定します。

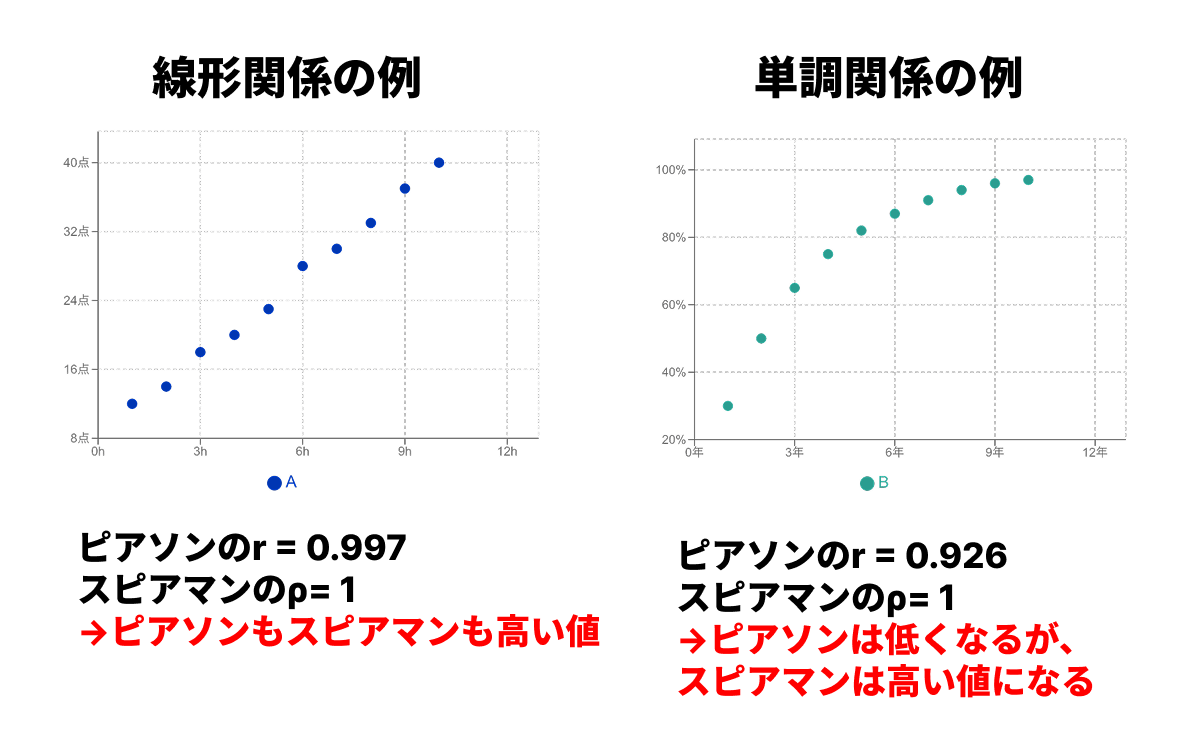
例えば、右側のグラフのように、最初は急激に、その後ゆるやかに増加するような関係（曲線的な関係）の場合、ピアソンの相関係数は低くなります。しかし、「Xが増えればYも増える」という単調な傾向は一貫しているため、スピアマンの順位相関係数は高い値を示します。

違い③：外れ値への耐性

ピアソンの相関係数は、データの中に極端に大きい、または小さい値（外れ値）があると、その値に強く引っ張られてしまいます。

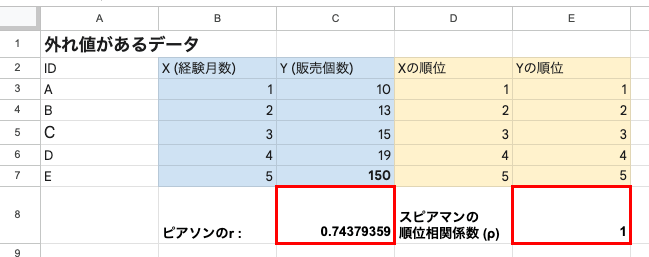
スピアマンは、実際の数値ではなく「順位」を使います。例えば、「10, 20, 30, 1000」というデータも、順位に直せば「1位, 2位, 3位, 4位」です。「1000」という外れ値が「100」であっても順位は変わらないため、外れ値の影響を受けにくい（頑健性が高い）というメリットがあります。

[外れ値のあるデータでの相関係数の比較]

スピアマンの順位相関係数の計算方法

スピアマンの順位相関係数（ρ、ローと読みます）は、どのように計算されるのでしょうか？ 概念を理解するために、簡単なステップを見てみましょう。

ステップ1：データを順位（ランク）に変換する

まず、2つの変数（XとY）のデータを、それぞれ小さい（または大きい）順に並べ替え、順位をつけます。

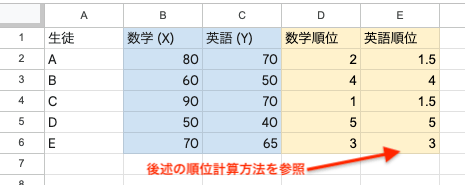
ステップ2：順位の差（D）を求める

次に、各データ（各個人）の「Xの順位」と「Yの順位」の差（D）を計算します。

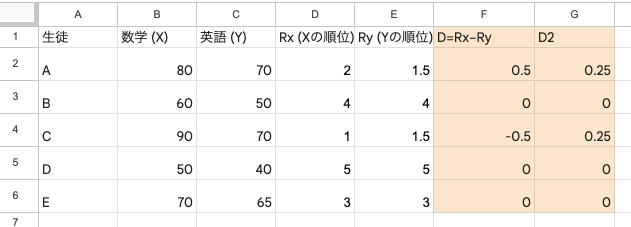
ステップ3：計算式に当てはめる

データの数（N）と、ステップ2で求めた順位の差（D）を使って、以下の式で計算します。

計算式：$\rho = 1 - \frac{6 \times \Sigma D^2}{N \times (N^2 - 1)}$

※ΣD² は、全員分のDを2乗して合計した値です

値を代入: $\rho = 1 - \frac{6 \times 0.5}{5 \times (5^2 - 1)}$

計算結果: $\rho = 0.975$

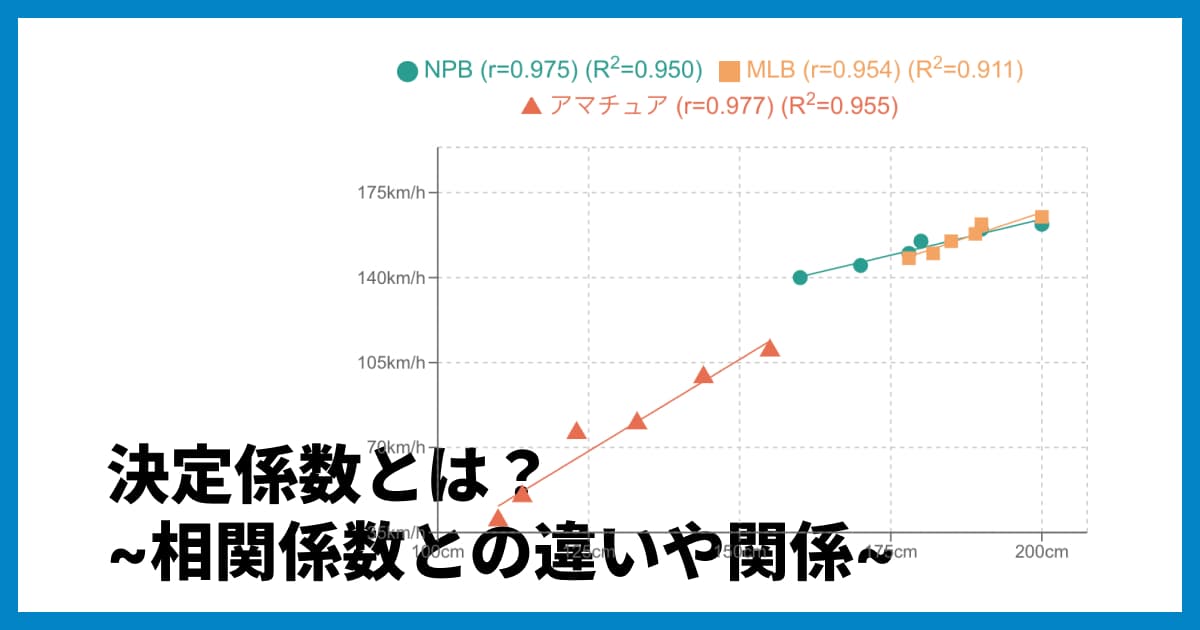
この計算により、ピアソンの相関係数を「順位データ」で計算した値とほぼ同じ結果（0.975）が得られます。

同順位（タイ）がある場合の注意点

もしデータに同じ値（例：70点の人が2人いる）が含まれる場合を「同順位（タイ）」と呼びます。この場合、順位は平均値を使います（例：3位と4位なら、(3+4)÷2 = 3.5位）。

タイが多い場合は、上記の式ではなく、タイを補正するための少し複雑な計算式（またはピアソンの積率相関係数の計算式を順位データに適用する方法）が用いられます。

Excelの場合は以下のように関数を使用することができます。

Excelでのタイ順位の処理方法

• ステップ1: RANK.AVG 関数を使う。 「タイ処理」部分に該当します。この関数が、同順位を自動で「1.5」のように補正した順位リストを作成します。

• ステップ2: CORREL 関数を使う。 ステップ1で作成した2つの順位リスト（Xの順位, Yの順位）に対して、CORREL（ピアソンの相関係数）を適用します。

この「RANK.AVG + CORREL」の組み合わせが、Excelでタイの影響を正確に処理したスピアマンの順位相関係数を求める方法です。

結果の解釈と目安

スピアマンの順位相関係数（ρ）も、ピアソンと同様に -1から+1までの値をとります。

• +1に近い: 強い「正の単調関係」がある。（一方が増えると、もう一方も増える傾向が強い）

• -1に近い: 強い「負の単調関係」がある。（一方が増えると、もう一方は減る傾向が強い）

• 0に近い: 単調関係はほとんどない。

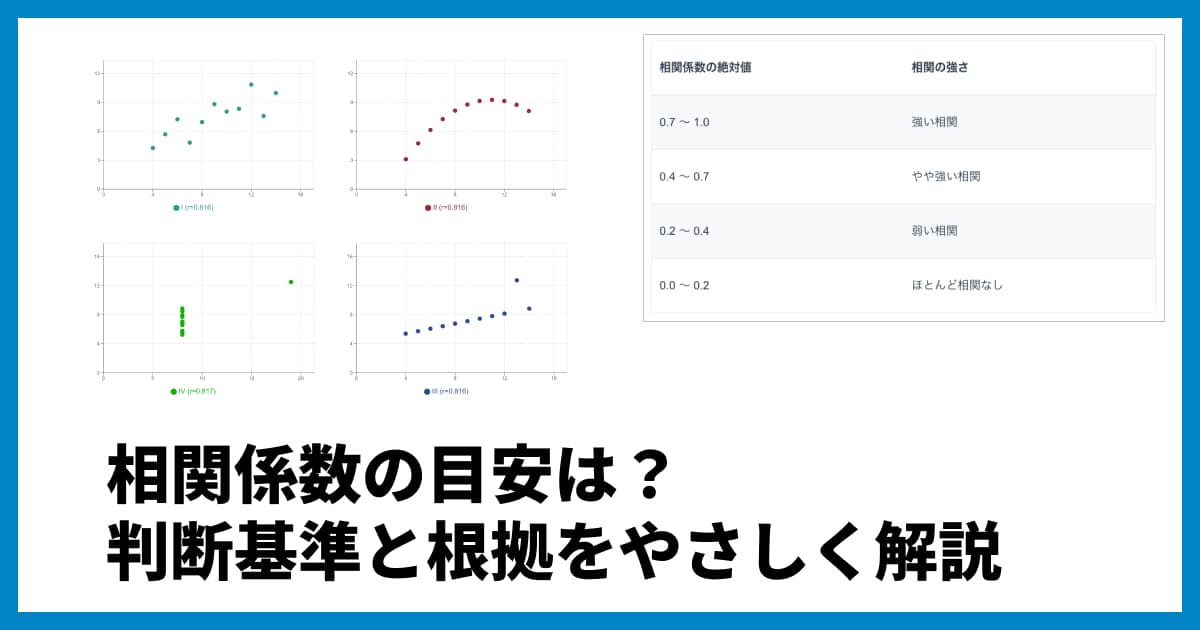
相関の強さの目安

相関の強さを判断するための絶対的な基準はありませんが、一般的に以下のような目安が使われることがあります。

>> 相関係数の目安やその根拠についての解説

有意性（p値）の確認

相関係数が0でなくても、それが「たまたま」そうなっただけ（誤差）の可能性もあります。そのため、統計的には「p値（有意確率）」を合わせて確認します。

p値が特定の基準（一般的に0.05）より小さい場合、「その相関は偶然ではなく、統計的に意味のある（有意な）関係だ」と判断します。

>> 相関係数とp値の意味とは？

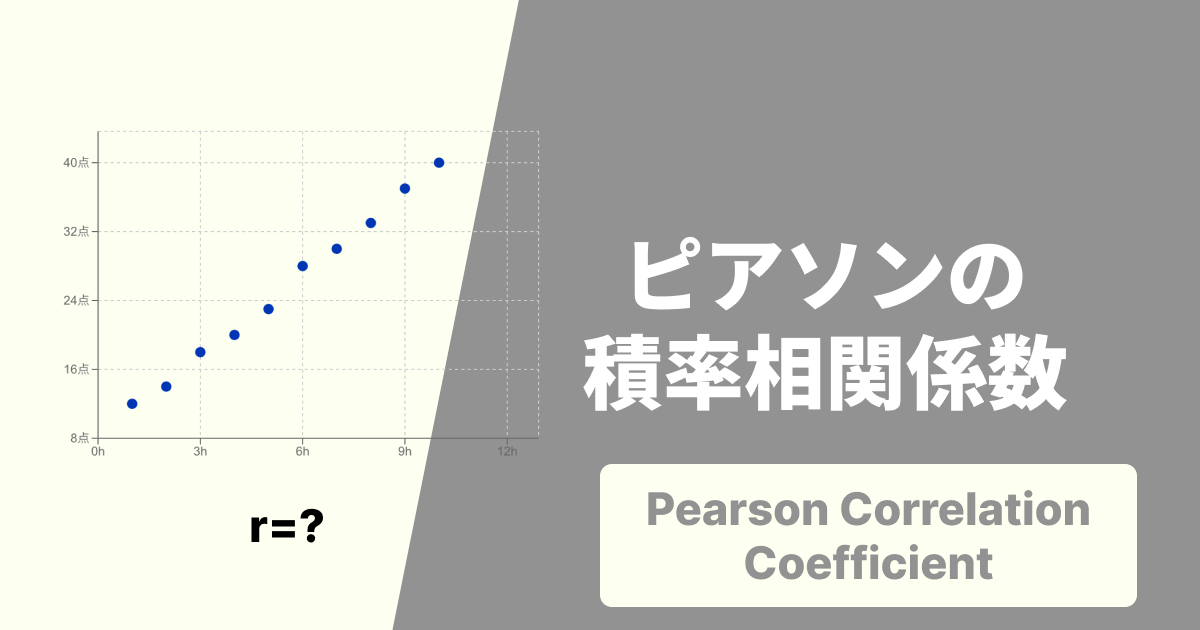
散布図で「単調関係」を視覚化しよう

スピアマンの順位相関係数は、数値だけを見ても関係性のイメージが湧きにくいかもしれません。そこで役立つのが「散布図」です。

上記のようなグラフ（単調関係）は、スピアマンの順位相関係数が高い典型例です。相関係数を計算するだけでなく、散布図でデータを視覚化し、どのような関係性があるかを自分の目で確認することが非常に重要です。

オンラインで素早く散布図を作成したい場合は、xGrapherの散布図作成ツールが便利です。データをコピー＆ペーストするだけで、2つの変数の関係性をすぐに可視化できます。

また、ExcelやGoogleスプレッドシートを使った散布図の作成方法は、以下の記事でも詳しく解説しています。

• Excelで散布図を作成する方法

• Googleスプレッドシートで散布図を作成する方法

まとめ

今回は、スピアマンの順位相関係数について解説しました。最後に要点をまとめます。

• スピアマンは、実際の数値ではなく「順位」データに基づいて計算する相関係数です。

• ピアソンが「線形関係」を見るのに対し、スピアマンは「単調関係」（一貫して増加または減少する傾向）を見ます。

• 順序尺度（満足度など）や、正規分布しないデータ、外れ値が気になる場合に特に有効です（ノンパラメトリック）。

• 値の解釈（-1〜+1）はピアソンと似ていますが、「単調関係」の強さを示していると理解することが重要です。

• 相関係数を求めたら、必ず散布図を作成して、実際のデータの関係性を視覚的に確認しましょう。

スピアマンの順位相関係数に関するQ&A

Q1. ピアソンの相関係数とスピアマンの順位相関係数は、どちらを使うべきですか？

A1. データの性質によります。データが間隔尺度・比例尺度であり、散布図を見て「直線的な関係」が想定でき、正規分布している（またはサンプルサイズが大きい）場合は、ピアソンを使います。
データが「順序尺度」である場合、散布図で「直線的ではないが単調な関係」が見られる場合、または「外れ値の影響」を避けたい場合は、スピアマンが適しています。

Q2. スピアマンの順位相関係数が「1」になるのは、どのような場合ですか？

A2. 2つの変数の「順位」が完全に一致した場合です。例えば、Xの順位が (1, 2, 3, 4, 5) で、Yの順位も (1, 2, 3, 4, 5) の場合です。元の数値が曲線的な関係でも、順位が一致していれば1になります。

Q3. 「単調関係」とは何ですか？

A3. 「一方が増加するとき、他方も常に増加する（または常に減少する）」関係のことです。増加（減少）の幅は一定である必要はありません（直線でなくてもよい）。

Q4. Excelでスピアマンの順位相関係数を計算する方法は？

A4. Excelにはスピアマンの順位相関係数を直接計算する簡単な関数（SPEARMANなど）は標準で用意されていません。
方法としては、①RANK.AVG関数を使って各データの順位を計算し、その順位データに対してCORREL関数（ピアソンの相関係数）を適用する、②分析ツール（アドイン）を使う、などの方法があります。

Q5. スピアマンの相関係数とケンドールのタウ（τ）の違いは何ですか？

A5. ケンドールの順位相関係数（ケンドールのタウ）も、スピアマンと同様に順位データに基づくノンパラメトリックな相関係数です。計算方法が異なり、ケンドールは「ペアの順序が一致しているか（順相）、逆転しているか（逆相）」に着目します。一般的にスピアマンの方がケンドールよりも値が少し大きくなる傾向があります。同順位（タイ）が多いデータの場合は、ケンドールが推奨されることもあります。

>> ケンドールの順位相関係数 ($\tau$)とは？計算方法も紹介