相関係数とp値の意味とは？「強さ」と「確かさ」の違いをわかりやすく解説

相関係数（r）：関係の「強さ」と「向き」を示す指標

まず、相関係数（r）は、2つの変数の間にある「直線的な関係の強さ」と「向き（方向）」を示す指標です。一般的に「相関係数」と言うと、ピアソンの積率相関係数を指すことが多いです。

>> 相関係数（r）の計算方法

相関係数（r）は、必ず -1 から +1 までの範囲の値をとります。

• r が +1 に近いほど：「強い正の相関」

  • 一方Vが増える（減る）と、もう一方も増える（減る）傾向が強い。

  • 例：勉強時間とテストの点数

• r が -1 に近いほど：「強い負の相関」

  • 一方が増えると、もう一方は減る傾向が強い。

  • 例：気温と暖房器具の売上

• r が 0 に近いほど：「相関がほとんどない（無相関）」

  • 2つの変数の間に直線的な関係は見られない。

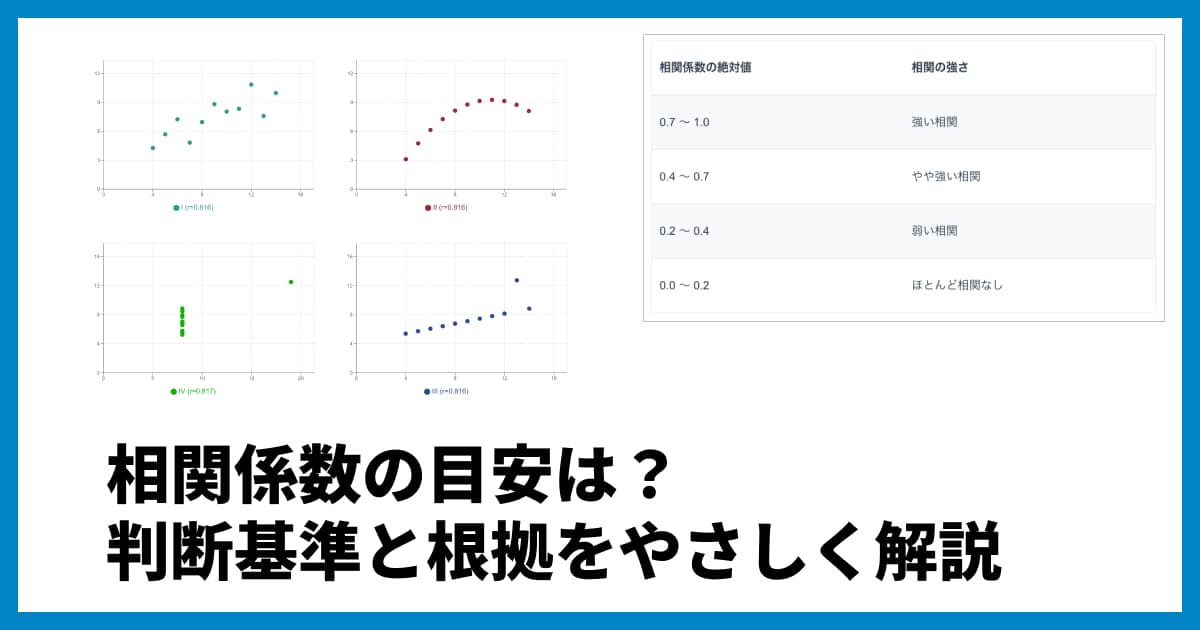
相関係数の目安

どのくらいの数値なら「相関が強い」と言えるかは分野によって異なりますが、一般的な目安として以下のように解釈されることが多いです。

重要なのは、相関係数はあくまで「関係の強さ」を示しているだけ、という点です。

>> 相関係数の目安とその根拠についての詳細解説

p値：相関の「確かさ（統計的有意性）」を示す指標

次に、p値です。これは「Probability Value（確率値）」の略で、相関分析においては「その相関が、統計的にどれだけ”確か”か」を示す指標です。

具体的には、「もし本当は2つの変数に全く相関がない（母集団の相関係数が0である）としたら、手元のデータ（サンプル）から観測されたような相関係数（またはそれ以上に極端な値）が、”偶然”得られてしまう確率」を示しています。

• p値が小さい（例：p = 0.01）

  • → 「もし本当に相関がないなら、こんなデータが偶然得られる確率はわずか1%だ」

  • → 「偶然とは考えにくい。この相関は”確か”そうだ」

  • → 統計的に有意な相関がある と判断します。

• p値が大きい（例：p = 0.20）

  • → 「もし本当に相関がないとしても、こんなデータが偶然得られる確率は20%もある」

  • → 「偶然こうなった可能性が十分にある。この相関は”確か”とは言えない」

  • → 統計的に有意な相関があるとは言えない と判断します。

p値の目安は「0.05（5%）」

統計の世界では、この「偶然か、確かか」のボーダーライン（有意水準）として、慣例的に p < 0.05（5%） がよく使われます。

p値が0.05を下回っていれば、「偶然起こる確率は5%未満なので、この相関は統計的に有意（＝偶然ではない、意味のある関係）と見なしましょう」と判断することが多いのです。

【重要】相関係数とp値のよくある誤解

ここが最も重要なポイントです。
相関係数（r）は「関係の強さ」、p値は「関係の確かさ」を示しており、この2つは別々の概念です。

データ分析のゴールは、「強くて、かつ確かな関係」を見つけることです。

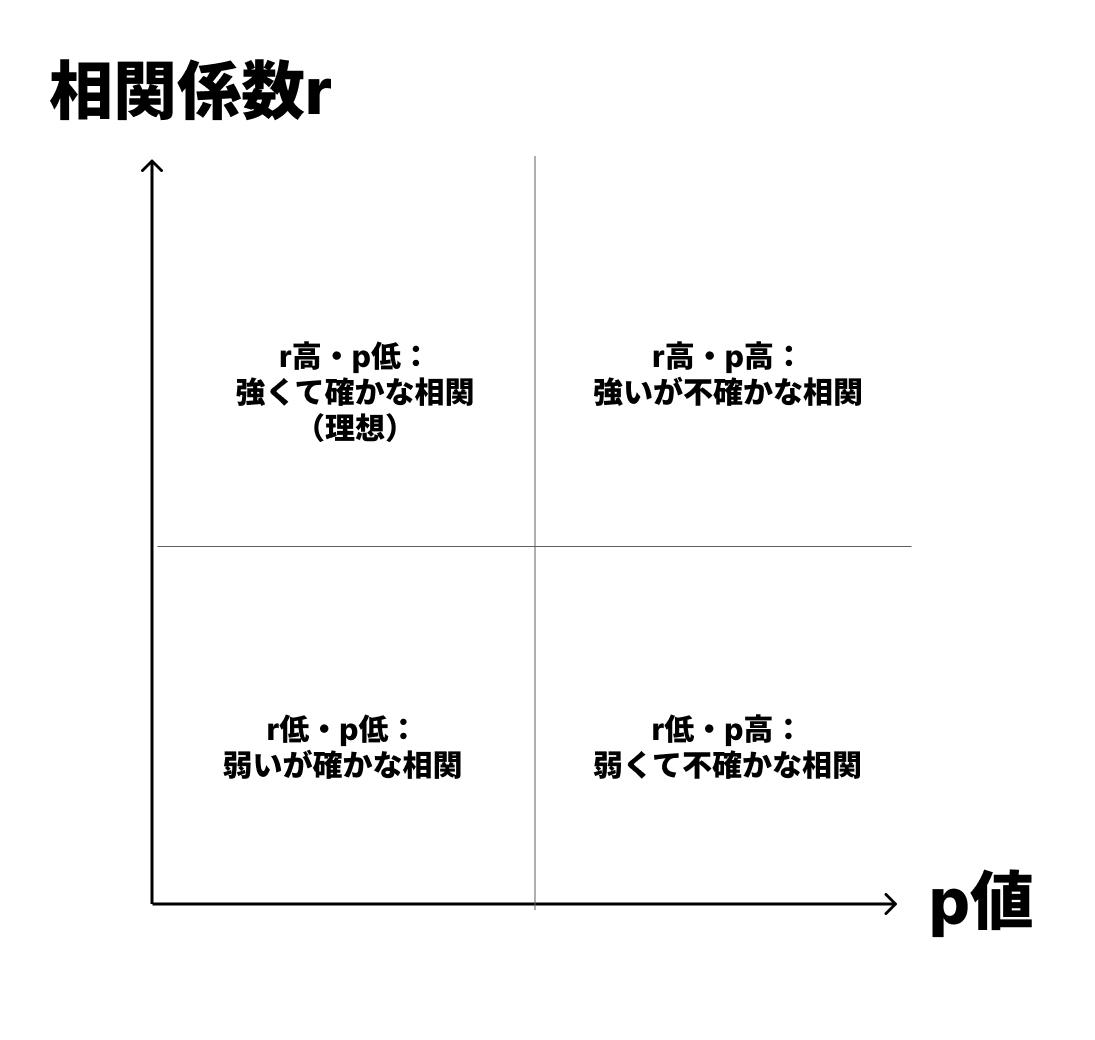
よくある誤解は、「強さ」と「確かさ」を混同してしまうことです。

誤解1：「相関係数が高い（r=0.8）なら、p値は必ず低い（有意になる）」？

答えは「No」です。

例えば、データ数が非常に少ない場合（サンプルサイズが小さい場合）、相関係数が高くてもp値は高くなる（有意にならない）ことがあります。

• 例：3人の生徒の「勉強時間」と「点数」を調べたら、たまたまr=0.9になった。

• → データが3人だけでは、「本当に相関がある」のか「たまたまその3人がそうだっただけ」なのか判断できません。

• → p値は高くなり、「統計的に有意とは言えない」という結果になります。

「強い」かもしれないが、「確か」ではない状態です。

誤解2：「p値が低い（p<0.01）なら、相関は必ず強い（r=0.7以上）」？

答えは「No」です。

例えば、データ数が非常に多い場合（サンプルサイズが大きい場合）、相関係数が非常に低くてもp値は低くなる（有意になる）ことがあります。

• 例：10万人のデータを調べたら、r=0.05（非常に弱い相関）だが、p<0.001になった。

• → データが10万人もいるので、「相関が全くのゼロ」ではなく、「（ごくわずかだが）確かに0ではない相関がある」と統計的に言えてしまいます。

• → しかし、r=0.05という「弱い」関係に、実用的な意味があるかは別問題です。

「確か」ではあるが、「弱い」状態です。

このように、相関係数（r）とp値は、サンプルサイズ（n）を介して互いに影響し合います。分析結果を見るときは、必ず「rの値」「p値」「サンプルサイズ」の3つをセットで確認する癖をつけましょう。

相関係数のp値はどのように計算される？

相関係数のp値は、「① 観測された相関係数（r）」と「② サンプルサイズ（n）」の2つの数値を使って計算されます。

手計算で求めることも可能ですが、通常は統計ソフトやツールが自動的に計算してくれます。計算の背景にある考え方は以下の通りです。

p値計算の基本的な流れ

1. 「もし本当は相関がない（母相関係数が0）」と仮定する。

これが統計的検定のスタート地点となる「帰無仮説」です。

2. 相関係数(r)とサンプルサイズ(n)から「t統計量」を計算する。

t統計量とは、「観測された相関(r)が、”相関ゼロ”から（偶然の範囲を超えて）どれだけ離れているか」を評価するための指標です。

• 相関係数(r)が0から遠い（1や-1に近い）ほど、t統計量は大きくなります。

• サンプルサイズ(n)が大きいほど、t統計量は大きくなります（＝少しの相関でも「意味がある」と見なされやすくなります）。

3. t分布を使って確率（p値）を計算する。

t統計量が従うとされる「t分布」（サンプルサイズを考慮した確率分布）を使い、「ステップ2で計算したt統計量、またはそれ以上に極端な値（珍しい値）が、偶然発生する確率」を求めます。

4. この確率が「p値」。

この計算結果の確率がp値です。もしp値が0.03なら、「もし本当に相関がないとしたら、今観測されているような相関（またはそれ以上）が偶然起こる確率は3%しかない」という意味になります。

実際にはどう計算する？

この計算を手作業で行うのは非常に複雑です。

※相関係数(r)自体の計算は「相関係数の計算方法」で解説しています。）

ExcelCORREL関数やGoogleスプレッドシートPEARSON関数では相関係数(r)は求められますが、p値を直接計算するシンプルな関数は標準で用意されていません。

実務では、以下のような統計解析機能を持つツールを使うのが一般的です。

• 統計解析ソフト（SPSS, R, JMPなど）

• Python (Scipyライブラリ) の scipy.stats.pearsonr 関数

• Excelの「データ分析」アドイン機能（回帰分析など）

p値の計算はツールに任せ、私たちは「p値がrとnから計算されている」という事実と、「p値が低いほど、その相関は偶然ではない（確からしい）」という意味を理解しておくことが重要です。

まずは「散布図」で可視化しよう

相関係数（r）とp値という数字だけを見て判断するのは危険な場合があります。なぜなら、相関係数（特にピアソンの積率相関係数）は、「直線的な」関係しか捉えられないからです。

例えば、下の図を見てください。

このデータでは、相関係数(r)はほぼ0になり、「相関なし」という結果になるかもしれません。しかし、グラフ（散布図）で見れば、明らかに「U字型」の強い関係性があることがわかります。

データを分析する際は、いきなり相関係数やp値を計算するのではなく、まずは散布図を作成して、データ全体の傾向や外れ値の有無を視覚的に確認することが非常に重要です。

xGrapherで簡単に散布図を作成

オンライングラフ作成ツールの xGrapher なら、データをコピー＆ペーストするだけで、誰でも簡単に高機能な散布図を作成できます。

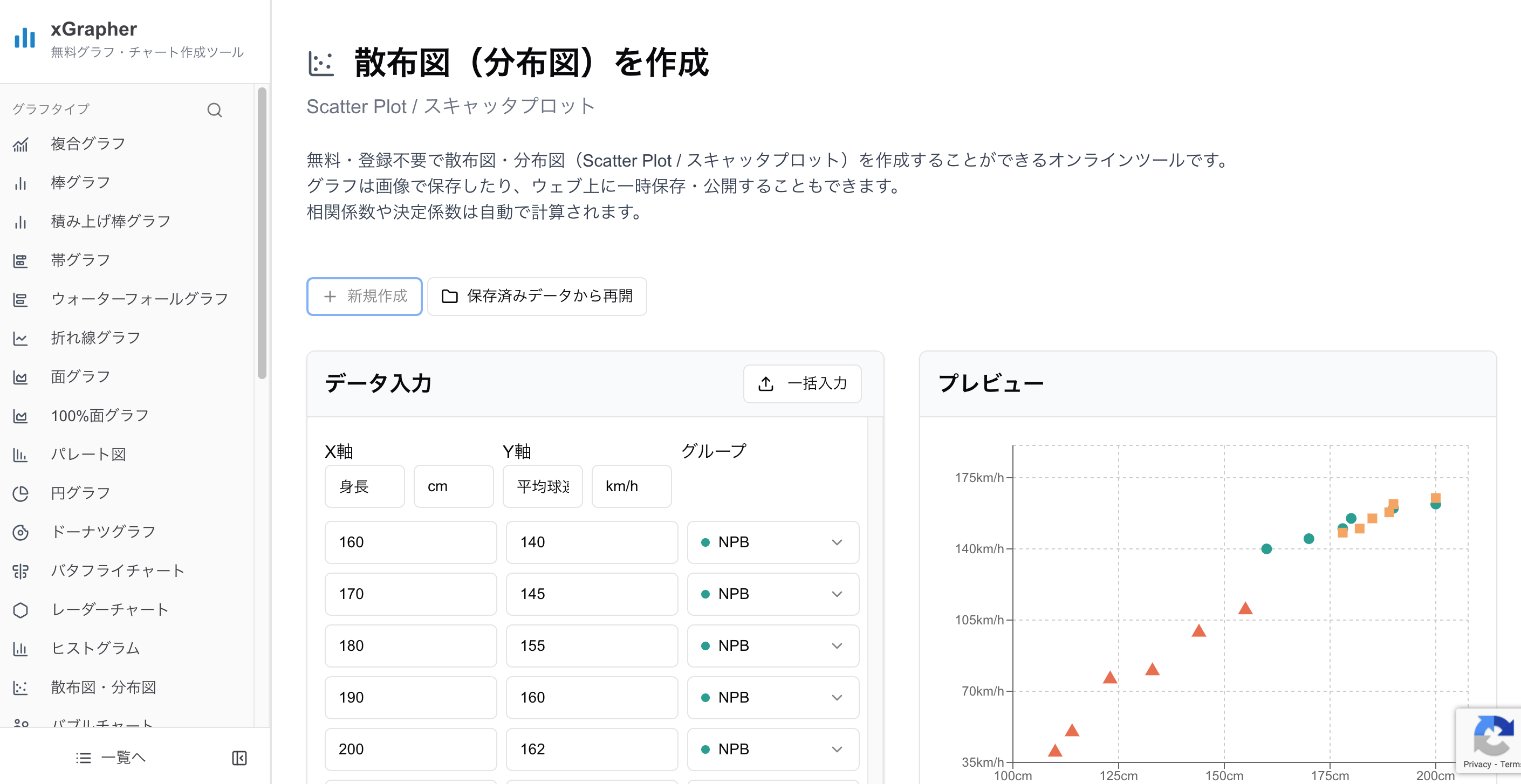
相関係数やp値を計算する前に、まずはxGrapherの散布図メーカーを使って、あなたのデータがどのような関係にあるのかを可視化してみましょう。

まとめ：相関係数とp値を正しく使いこなすために

今回は、相関分析における「相関係数(r)」と「p値」の違いについて解説しました。

• 相関係数（r）

  • 役割: 2つの変数の「関係の強さ」と「向き」を示す。

  • 見方: -1から+1の範囲。絶対値が1に近いほど強い。

• p値

  • 役割: その相関が偶然ではないか、「関係の確かさ（統計的有意性）」を示す。

  • 見方: 0から1の範囲。一般的に0.05（5%）未満なら「有意」と判断する。

最も重要なのは、両方の指標を組み合わせて総合的に判断することです。

• 「r=0.8, p=0.01」（強くて、確かな相関）

• 「r=0.2, p=0.01」（弱いが、確かな相関。サンプルサイズが大きい可能性）

• 「r=0.8, p=0.10」（強いかもしれないが、不確かな相関。サンプルサイズが小さい可能性）

そして、これらの数字を見る前に、必ず散布図でデータを可視化することを忘れないでください。

相関係数とp値に関するQ&A

Q1: 相関係数が0.8で、p値が0.1でした。これはどう解釈すればいいですか？

A1: 「関係性は強い（r=0.8）ように見えるが、統計的に確かとは言えない（p=0.1 > 0.05）」と解釈します。これは、データ数（サンプルサイズ）が少ないために、その「r=0.8」という結果が偶然である可能性を否定しきれない状況です。データを増やすことで、p値が下がり、有意な結果になる可能性があります。

Q2: 相関係数が0.1で、p値が0.01でした。これは「強い相関あり」と言えますか？

A2: いいえ、「弱い相関だが、統計的には有意（確か）である」と解釈します。p値が0.01と低いため、この「r=0.1」という相関は偶然ではなく、確かに存在すると言えます。ただし、相関の「強さ」自体は非常に弱いです。これはデータ数（サンプルサイズ）が非常に多い場合によく見られます。

Q3: p値は小さければ小さいほど良いのですか？

A3: p値が小さいほど「偶然ではない」という「確かさ」は増します（例：p=0.001はp=0.04よりも確かです）。しかし、Q2のように、p値が非常に小さくても相関係数(r)が低ければ「弱い関係」であることに変わりはありません。p値の小ささだけをもって「良い分析結果」とは判断できません。

Q4: ExcelやGoogleスプレッドシートでp値を計算できますか？

A4: Excelやスプレッドシートで相関係数(r)を計算するのは簡単ですが（CORREL関数など）、相関係数に対するp値を直接計算する簡単な関数は標準で用意されていません（回帰分析の機能を使えば可能）。統計解析ソフト（R, Python, SPSSなど）を使うか、xGrapherのようなツールで相関係数（決定係数）と散布図を同時に確認するのが手軽です。

Q5: ピアソンの相関係数以外（スピアマンなど）でもp値は出ますか？

A5: はい、出ます。スピアマンの順位相関係数やケンドールの順位相関係数など、他の相関係数にも「その相関係数が0である」という帰無仮説に対するp値を計算することができます。

参考記事:
スピアマンの順位相関係数とは
ケンドールの順位相関係数とは