決定係数(R²)とは？目安・計算式・相関係数との違いをわかりやすく解説
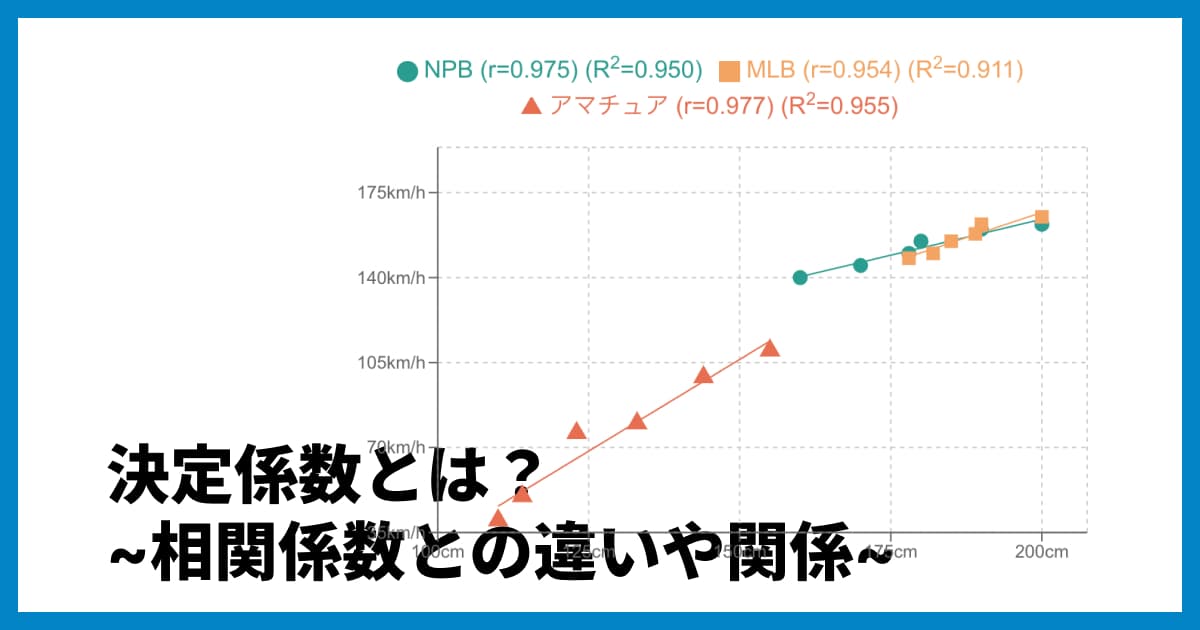
データ分析をしていると、「決定係数 ()」や「相関係数 ()」という言葉をよく目にします。特に回帰分析（予測モデル）を作った際、そのモデルがどれだけ良いかを示す指標として決定係数が登場します。
でも、「相関係数と何が違うの？」「 の値が0.7だったけど、これって良いの？」と疑問に思う方も多いのではないでしょうか。
この記事では、データ分析の初心者の方にもわかりやすく、決定係数の基本的な意味から、相関係数との違い、そして両者の関係性について、グラフのイメージを交えながら解説していきます。
この記事の内容（目次）
決定係数と相関係数の決定的な違い
決定係数と相関係数は、どちらもデータ間の関係性を示す指標ですが、その「役割」が根本的に異なります。まずはそれぞれの役割を明確にしましょう。
相関係数（r）とは？
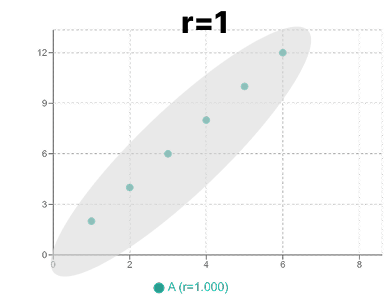
相関係数（ピアソンの積率相関係数、）は、「2つのデータ（変数）間の『直線的な』関係の強さと向き」 を示す指標です。
値の範囲: -1から+1までです。
+1に近い: 強い「正の相関」があります。（例：身長が高い人ほど、体重も重い傾向）
-1に近い: 強い「負の相関」があります。（例：気温が低い日ほど、暖房費が高い傾向）
0に近い: 2つのデータ間に「直線的な」関係はほとんどありません。
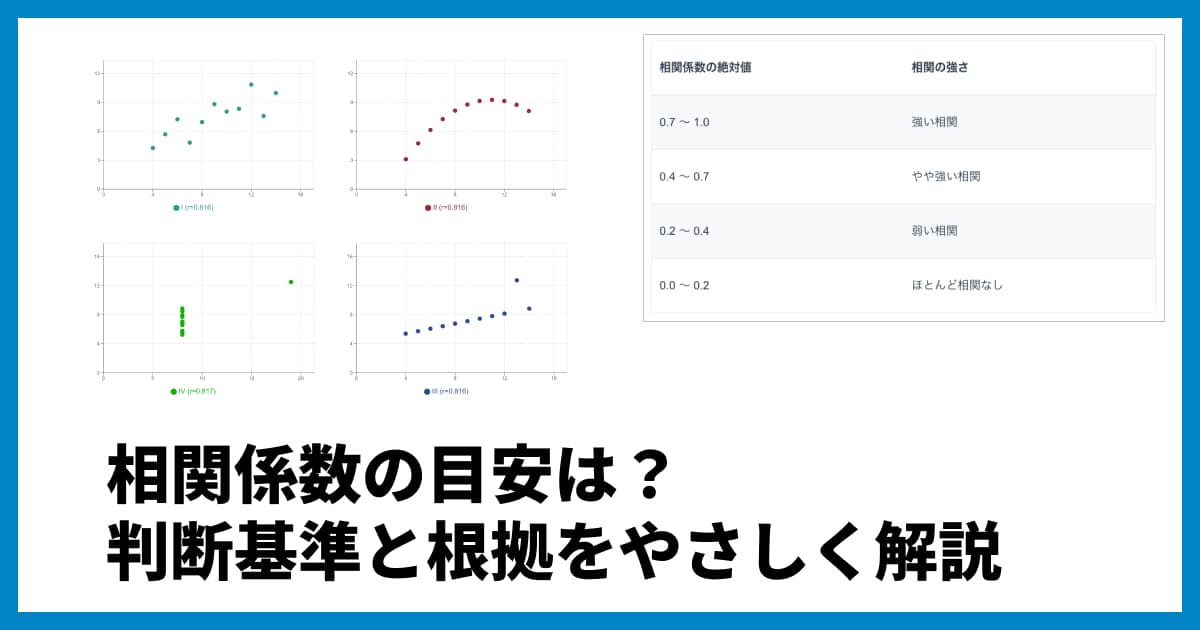
あくまで「直線的な関係」を見ている点がポイントです。もしデータがきれいなU字型になっていても、直線的な関係ではないため相関係数は0近くになることがあります。
>> 相関係数の目安やその根拠についての解説
相関係数について詳しくは、こちらの記事「相関係数とは？意味と目安、計算方法をわかりやすく解説」もご覧ください。
決定係数 (R²) とは？
決定係数 (、R-squared、アールスクエアとも呼ばれます）は、「予測モデルの『当てはまりの良さ』」 を示す指標です。一般的に回帰分析で使われます。
もう少し具体的に言うと、「予測したいデータ（目的変数）の変動のうち、どれくらいの割合を予測モデル（説明変数）で『説明』できているか」 を示します。
値の範囲: 基本的に0から1までです。（%で表すこともあります）
1に近い (例: 0.9): モデルがデータの変動をほぼ完璧に説明できている（当てはまりが非常に良い）。予測精度が高いと言えます。
0に近い (例: 0.1): モデルがデータの変動をほとんど説明できていない（当てはまりが悪い）。そのモデルは予測に使えない可能性が高いです。
例えば、決定係数 だった場合、「予測したいデータのバラツキの70%は、この予測モデルで説明できていますよ」という意味になります。
相関係数と違い、「向き（プラスかマイナスか）」の情報はなく、純粋に「どれだけ説明できているか（当てはまりの良さ）」だけを示します。
決定係数の計算式と求め方
決定係数R²の意味をより深く理解するために、計算式を見てみましょう。難しい数式に見えるかもしれませんが、考え方はシンプルです。
基本の計算式
決定係数は以下の式で定義されます。
ここで登場する3つの「変動」を理解することがポイントです。
記号 | 名称 | 意味 | 計算式 |
|---|---|---|---|
SST | 全変動 (Total Sum of Squares) | データ全体のバラツキ | 各データと全体平均の差の二乗の合計 |
SSR | 回帰変動 (Regression Sum of Squares) | モデルで説明できたバラツキ | 各予測値と全体平均の差の二乗の合計 |
SSE | 残差変動 (Error Sum of Squares) | モデルで説明できなかったバラツキ | 各データと予測値の差の二乗の合計 |
yi : 実際のデータの値
ȳ : データ全体の平均値
ŷi : 回帰モデルによる予測値
これら3つの変動には、次の関係が成り立ちます。
つまり「データ全体のバラツキ ＝ モデルで説明できた分 ＋ 説明できなかった分」ということです。
この関係を使うと、決定係数は次のようにも書けます。
この式を見ると、決定係数は「全体のバラツキのうち、モデルで説明できた割合」であることが直感的にわかりますね。
寄与率としての決定係数
決定係数は「寄与率」とも呼ばれます。これは「説明変数が目的変数の変動にどれだけ寄与（貢献）しているか」をパーセンテージで表す考え方です。
例えばであれば、「説明変数は目的変数の変動の64%を説明（寄与）している」と解釈できます。統計学の教科書では「決定係数」、品質管理や実験計画法の分野では「寄与率」と呼ばれることが多いですが、意味は同じです。
具体的な計算例
5つのデータ点
で実際に計算してみましょう。
Step 1: 平均値を求める
Step 2: 回帰直線を求める
最小二乗法で回帰直線を計算すると、ŷ = 0.6x + 2.2となります。
各 x に対する予測値 ŷは次の通りです。
x | y（実測値） | ŷ（予測値） |
|---|---|---|
1 | 2 | 2.8 |
2 | 4 | 3.4 |
3 | 5 | 4.0 |
4 | 4 | 4.6 |
5 | 5 | 5.2 |
Step 3: 各変動を計算する
SST（全変動） = (2−4)² + (4−4)² + (5−4)² + (4−4)² + (5−4)² = 4+0+1+0+1 = 6.0
SSR（回帰変動）= (2.8−4)² + (3.4−4)² + (4.0−4)² + (4.6−4)² + (5.2−4)² = 1.44+0.36+0+0.36+1.44 = 3.6
SSE（残差変動） = (2−2.8)² + (4−3.4)² + (5−4.0)² + (4−4.6)² + (5−5.2)² = 0.64+0.36+1.0+0.36+0.04 = 2.4
検算: SSR + SSE = 3.6 + 2.4 = 6.0 = SSTですので、正しく計算できていますね。
Step 4: 決定係数を求める
R² = 1 − SSE ÷ SST = 1 − 2.4 ÷ 6.0 = 1 − 0.4 = 0.6
つまり、この回帰直線はデータの変動の60%を説明できているということです。
決定係数と相関係数の「関係」とは？（R² = r²？）
「決定係数 相関係数」と検索する方が最も知りたいのが、この2つの関係性でしょう。
結論から言うと、「単回帰分析（説明変数が1つだけの予測モデル）の場合」においてのみ、
決定係数 () ＝ 相関係数 () の2乗
という関係が成り立ちます。
例:
「気温」だけから「アイスの売上」を予測する（単回帰分析）
気温とアイスの売上の相関係数 だった場合
予測モデルの決定係数 となります。
例 (負の相関の場合):
「広告費」だけから「競合の売上」を予測する（単回帰分析）
広告費と競合の売上の相関係数 だった場合
予測モデルの決定係数 となります。
相関係数が でも でも、2乗すれば同じ （ なら ）になりますね。
これは、相関係数のプラス・マイナスは「向き」を示しているだけで、「直線的な関係の強さ」自体は同じだからです。そのため、その直線を予測モデルとして使った場合の「当てはまりの良さ（説明できる割合）」も同じになる、とイメージすると分かりやすいでしょう。
注意点: 重回帰分析の場合は ではない
この の関係が成り立つのは、あくまで変数が1対1の「単回帰分析」の時だけです。
予測に使う説明変数が2つ以上ある場合（例：「気温」と「湿度」から「アイスの売上」を予測する）を「重回帰分析」と呼びます。
この場合、相関係数は2変数間でしか計算できないため、「相関係数の2乗 ＝ 決定係数」という単純な関係は成り立ちません。
重回帰分析で出てくる は、あくまで「モデル全体で、目的変数をどれだけ説明できているか」を示す指標となります。
決定係数 (R²) を使う際の目安と注意点
よく「R²が0.5以上なら意味がある」「0.8以上なら強い」と言われることがありますが、これは間違いです。決定係数の目安は、分析する分野によって大きく異なります。以下の表を参考にしてください。
分野 | R²の目安 | 備考 |
|---|---|---|
物理学・工学 | 0.95以上 | 制御された実験環境では非常に高い精度が求められる。$R^2 = 0.99$ でも不十分とされる場合がある |
生物学・医学 | 0.5〜0.8 | 生体データは個体差が大きく、バラツキが出やすい |
社会科学・経済学 | 0.3〜0.5 | 多数の変数が影響するため、単一モデルでの説明力に限界がある |
心理学・行動科学 | 0.1〜0.3 | 人間の行動は予測困難。$R^2 = 0.3$ でも重要な発見とされることがある |
絶対的な基準はありません。その分野の過去の研究と比較したり、予測の目的（高精度な予測が必要か、大まかな傾向が知りたいだけか）に応じて判断する必要があります。
決定係数が低いときの改善アプローチ
分析の結果、決定係数が想定より低かった場合は、以下の方法を検討してみましょう。
変数の追加（重回帰分析への発展）: 説明変数を1つだけでなく複数使うことで、モデルの説明力が向上する場合があります。例えば「気温」だけでなく「湿度」や「曜日」も加えてみるといった具合です。
非線形モデルの検討: データが直線的でない関係（曲線的な傾向）を持っている場合、多項式回帰や対数変換などの非線形モデルを試すとR²が改善することがあります。
外れ値の確認: 極端に外れたデータ（外れ値）が1つあるだけで、R²が大きく下がることがあります。散布図を見て外れ値がないか確認しましょう。外れ値を除外するかどうかは、そのデータが異常値なのか意味のある値なのかを慎重に判断する必要があります。
注意点: 自由度調整済み決定係数
決定係数 () には、「予測に使う説明変数を増やせば増やすほど、値が（当てはまりが良く見えて）高くなってしまう」という弱点があります。
たとえ予測に全く関係ない変数を適当に追加したとしても、 はわずかに上昇してしまう傾向があるのです。
これでは、本当に良いモデル（説明変数の組み合わせ）なのか判断できません。
そこで、モデルの「複雑さ（使った変数の数）」も考慮してペナルティを課した指標が「自由度調整済み決定係数（Adjusted ）」です。
複数の説明変数を使う重回帰分析で、どのモデル（変数の組み合わせ）が良いかを比較する際は、通常の ではなく、この自由度調整済み決定係数を見るのが一般的です。
決定係数と相関係数をグラフ（散布図）で確認しよう
決定係数も相関係数も、元は2つのデータの関係性を見ています。これらの指標を正しく理解するのに最適なグラフが「散布図」です。
散布図に「近似曲線（回帰直線）」を追加すると、データ全体の傾向が掴みやすくなります。そして、この近似曲線がデータ（点）にどれだけフィットしているかを示す数値が「決定係数 ()」です。
散布図の基本的な見方や作り方は、「散布図とは？見方や作成時のポイントを解説」や「散布図の見方を徹底解説！」で詳しく解説しています。
Excelやスプレッドシートでの表示方法
ExcelやGoogleスプレッドシートでも、散布図を作成し、グラフオプションから「近似曲線」を追加し、「 値をグラフに表示する」にチェックを入れることで簡単に確認できます。
詳しい手順は以下の記事も参考にしてください。
xGrapherで簡単に散布図を作成
もっと手軽に、Web上でデータを貼り付けるだけで美しい散布図や近似曲線、相関係数を確認したい場合は、xGrapher が便利です。
オンライングラフ作成ツールの xGrapher なら、データを入力するだけですぐに散布図を作成できます。
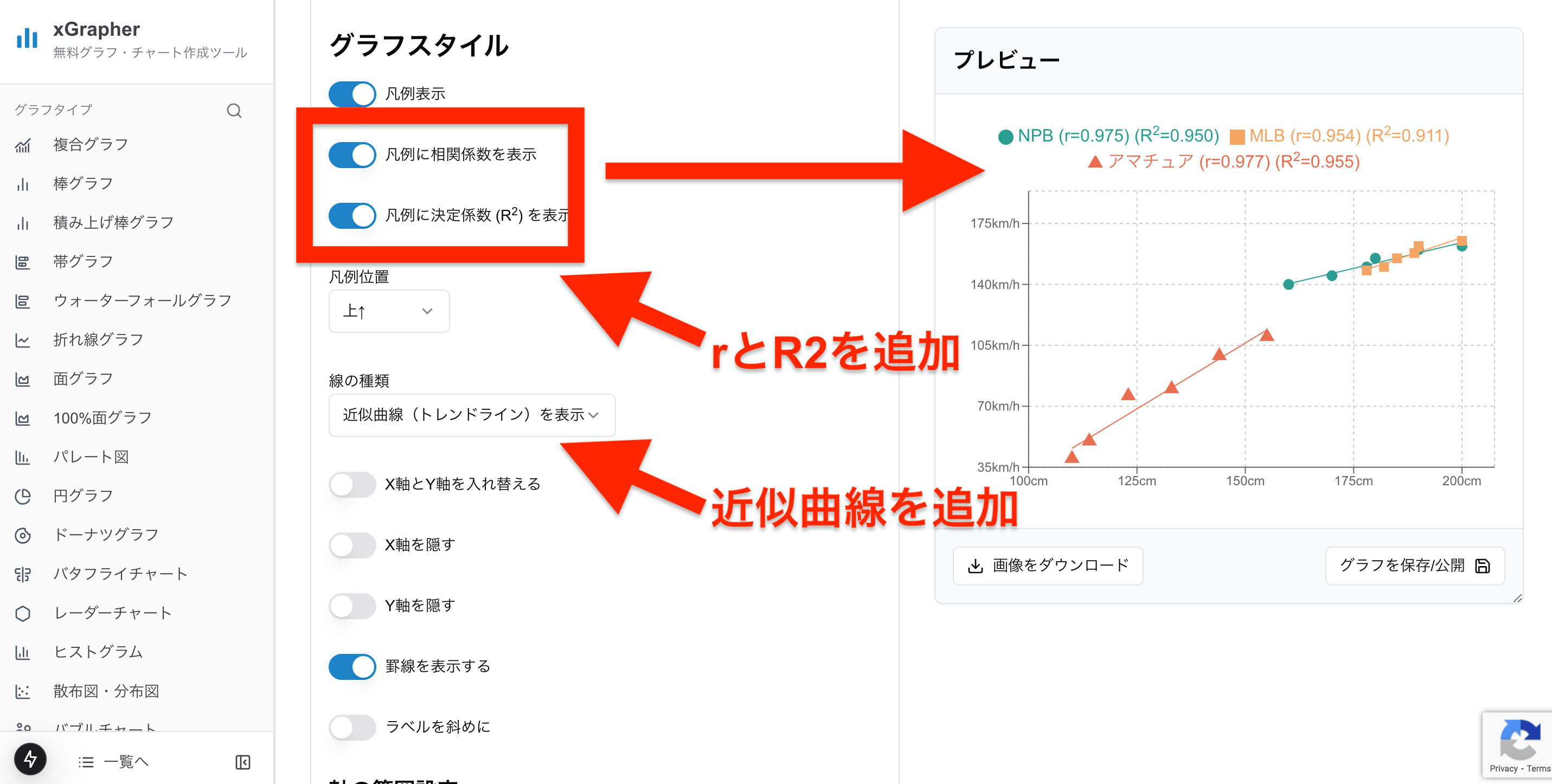
「xGrapherの散布図作成ツール」では、オプションで近似曲線や決定係数 () をグラフ上に表示することも可能です。
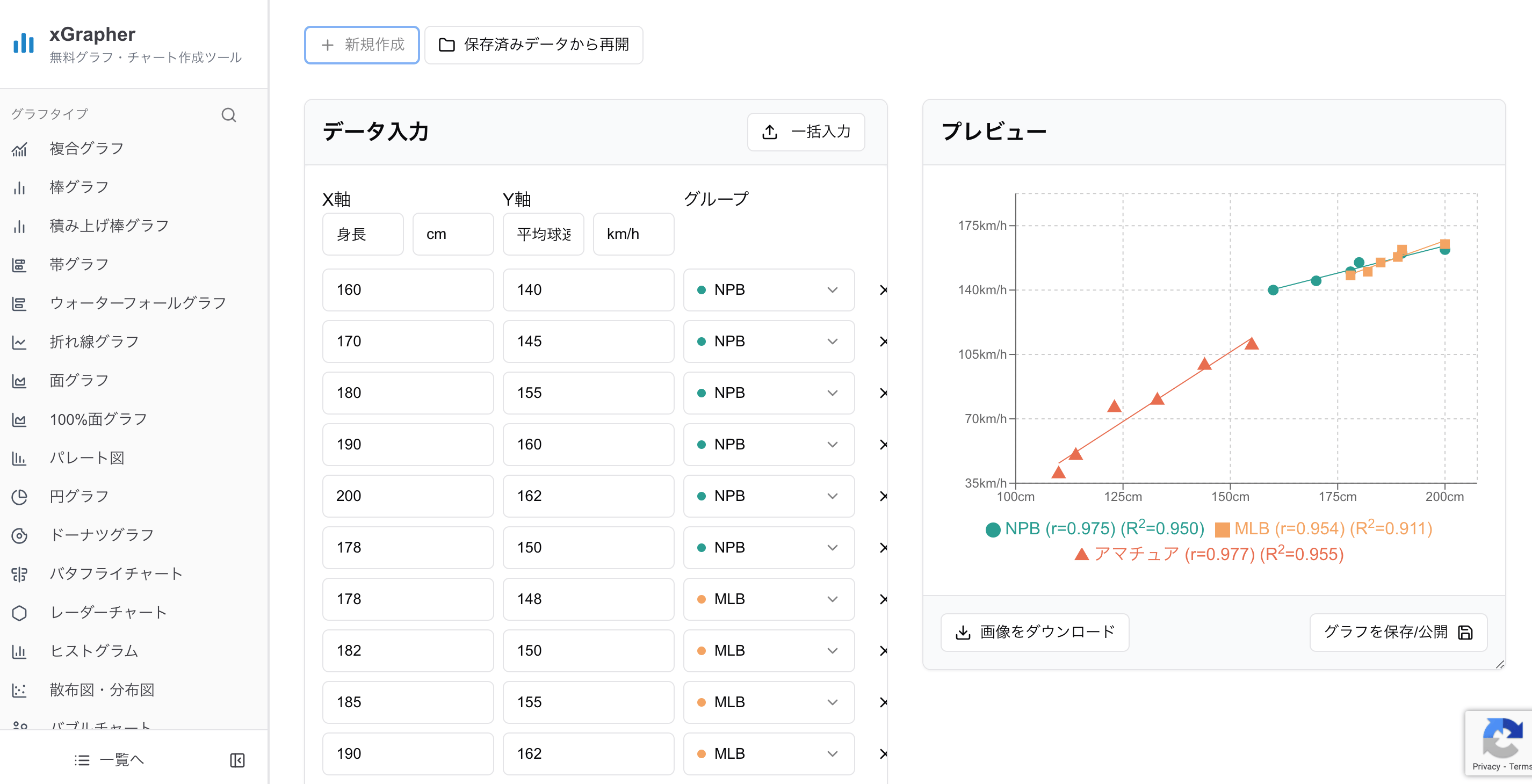
xGrapherを使った相関係数の計算や散布図の活用については、以下の記事でも紹介しています。
まとめ
最後に、決定係数と相関係数のポイントをおさらいしましょう。
相関係数 ():
2つのデータの「直線的な関係の強さ」と「向き（+/-）」を示す。-1〜+1の値をとる。決定係数 ():
予測モデルの「当てはまりの良さ（説明できる割合）」を示す。0〜1の値をとる。関係性:
「単回帰分析（説明変数が1つ）」の場合のみ、 が成り立つ。活用:
決定係数 の目安は分野による。重回帰分析では「自由度調整済み決定係数」を見る。視覚化:
どちらも「散布図」と「近似曲線」を使って視覚的に理解するのがおすすめです。xGrapherなどのツールを活用して、データ分析に役立てましょう。
決定係数・相関係数に関するQ&A
Q1: 決定係数がマイナスになることはありますか？
A1: 通常の（最小二乗法による）単回帰分析や重回帰分析では、決定係数 は0から1の間の値をとります。しかし、予測モデルが「平均値で予測する」よりも当てはまりが悪いという特殊なケース（例えば、切片を強制的に0にするモデルなど）では、理論上マイナスになることもあり得ます。また、「自由度調整済み決定係数」は、モデルに意味のない変数が多く含まれる場合などにマイナスになることがあります。
Q2: 決定係数と相関係数、どちらが重要ですか？
A2: 目的によります。単に「2つのデータに関係があるか（強さ・向き）」を知りたいだけなら相関係数が便利です。一方、「片方のデータを使って、もう片方のデータを予測するモデルを作りたい」場合、そのモデルの精度評価として決定係数が重要になります。
Q3: 相関係数が高い（例: 0.9）のに、決定係数が低いことはありますか？
A3: いいえ、単回帰分析（変数が1つ）の場合はありえません。上記で説明した通り、 の関係があるため、相関係数が高ければ決定係数も高くなります（ なら ）。
Q4: 相関係数が低い（例: 0.2）のに、決定係数が高いことはありますか？
A4: Q3と同じ理由で、単回帰分析の場合はありえません（ なら ）。ただし、データがU字型のような「直線的ではないが強い関係」を持つ場合、相関係数 は0に近くなりますが、非線形な予測モデル（多項式回帰など）を使えば高い決定係数 が得られる可能性はあります。
Q5: 決定係数が1になるのはどんな時ですか？
A5: 予測モデルが、実際のデータを完璧に予測できた時です。散布図で言えば、すべてのデータ（点）が、引かれた近似曲線（回帰直線）の上にピッタリと乗っている状態です。現実のデータ分析では滅多に起こりませんが、物理法則などではあり得ます。
