偏差値のグラフとは?分布がわかる正規分布とヒストグラムの簡単な作り方

「あなたの偏差値は55です」と言われた時、それが全体の中でどのくらいの位置にいるのか、具体的にイメージできるでしょうか?
偏差値は、テストの平均点を50、標準偏差を10として、自分が集団の中でどれくらいの位置にいるかを示す数値です。しかし、数字だけでは全体像を把握しにくいものです。
この記事では、偏差値の分布を「グラフ」で視覚化することの重要性と、その代表的なグラフである「正規分布曲線」や「ヒストグラム」についてわかりやすく解説します。自分の成績や集団の傾向を客観的に理解するために、グラフの力を活用してみましょう。
この記事の内容(目次)
偏差値はどうやって計算されるの?
偏差値は、テストの「素点(とくてん)」だけではわからない、集団内での相対的な位置を知るための数値です。以下の計算式で求められます。
少し難しく見えるかもしれませんが、ポイントは「平均点だった人を偏差値50にする」というルールです。
例えば以下のように計算できます。
得点: 70
平均点: 60
標準偏差: 10
→(70 - 60) × 10 + 50 = 60
それぞれの偏差値が上位何%にあたるかの目安は以下の通りです。
偏差値 | 上位 % (目安) | 1000人中の順位 (目安) |
85 | 約 0.02% | 約 1位 |
80 | 約 0.13% | 約 1位 |
75 | 約 0.62% | 約 6位 |
70 | 約 2.28% | 約 23位 |
65 | 約 6.68% | 約 67位 |
60 | 約 15.87% | 約 159位 |
55 | 約 30.85% | 約 309位 |
50 | 50.00% | 500位 |
45 | 約 69.15% | 約 691位 |
40 | 約 84.13% | 約 841位 |
35 | 約 93.32% | 約 933位 |
30 | 約 97.72% | 約 977位 |
25 | 約 99.38% | 約 994位 |
「標準偏差」とは?
計算式に出てくる「標準偏差(ひょうじゅんへんさ)」とは、集団の点数の「ばらつき具合」を示す数値です。
標準偏差が小さい:平均点付近に多くの人が集まっている(ばらつきが小さい)
標準偏差が大きい:点数が広範囲に散らばっている(ばらつきが大きい) 偏差値は、この「ばらつき具合(標準偏差)」も考慮して、「平均点からどれくらい離れているか」を客観的な数値で示してくれるのです。
標準偏差は以下の色で求めることができます。
偏差値のグラフ=「正規分布」のグラフです
偏差値について考えるとき、最もよく使われるのが「正規分布(せいきぶんぷ)」と呼ばれるグラフです。
左右対称の「山の形」
正規分布のグラフは、平均値(偏差値50)を頂点とした、左右対称のなめらかな「山の形(ベルカーブ)」をしています。
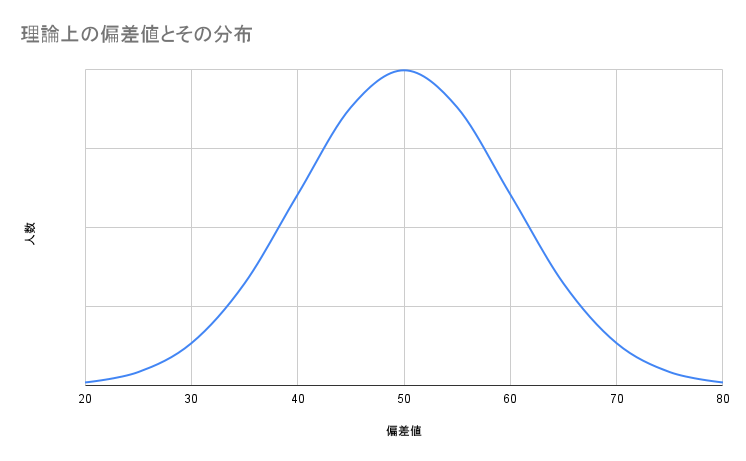
このグラフが示すのは、「どの偏差値の人が、どれくらいの割合で存在するのか」ということです。
最も多いのは偏差値50付近の人:グラフの山が一番高い部分です。
偏差値50から離れるほど、人数は少なくなる:山の裾野(すその)に向かって、グラフの高さは低くなっていきます。
偏差値と人数の割合
正規分布のグラフが示す「人数の割合」は、統計学の「標準偏差()」という考え方に基づいています。
偏差値は、平均が50、標準偏差(ばらつきの幅)が10になるように作られた数値です。
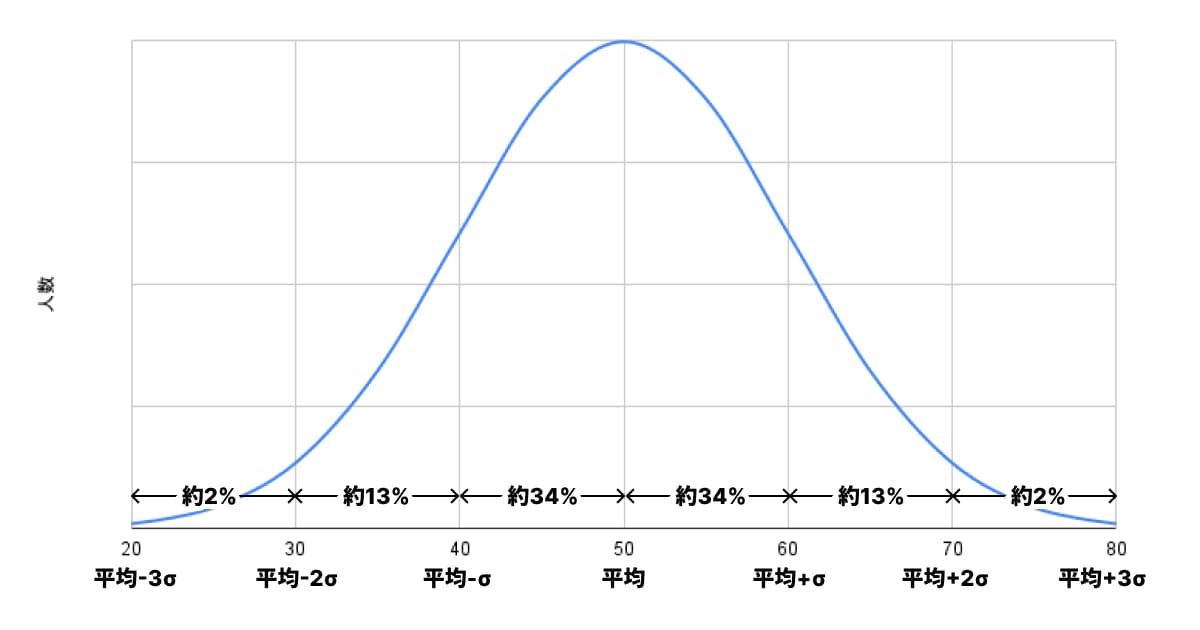
正規分布には、「平均値から標準偏差いくつ分離れた範囲内に、全体の何%のデータが含まれるか」という決まったルール(経験則)があります。
の範囲:全体の 約68.3% が含まれる
偏差値でいうと「」なので、偏差値40〜60の間です。
の範囲:全体の 約95.4% が含まれる
偏差値でいうと「」なので、偏差値30〜70の間です。
の範囲:全体の 約99.7% が含まれる
偏差値でいうと「」なので、偏差値20〜80の間です。
この統計的なルールがあるため、偏差値がわかると「全体の中でどのくらいの位置にいるか」が自動的にわかるのです。
例えば、偏差値60の人は、「平均(50) + 標準偏差1個分(10)」の位置にいます。
全体の約68.3%が偏差値40〜60の間にいるため、それよりも外側(偏差値60以上、または40以下)には約31.7%(100% - 68.3%)の人がいます。グラフは左右対称なので、その半分、つまり偏差値60以上の人は約15.8%(% 2)となります。
同様に、偏差値70()以上の人は、上位わずか約2.3%((100% - 95.4%) 2)であることがわかります。
「ヒストグラム」で見るテスト結果のばらつき
正規分布は、偏差値の「理想的な分布の形」を示したものです。では、実際のテスト結果(素点)の分布はどのようになっているのでしょうか?
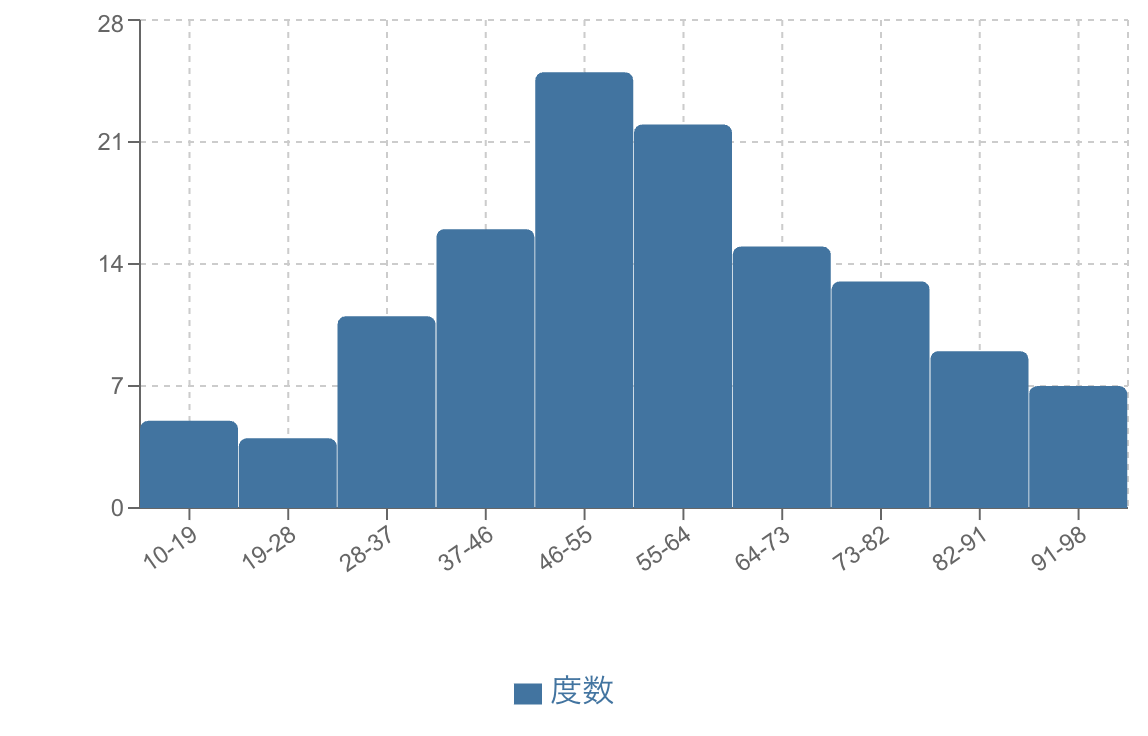
それを視覚化するのに最適なグラフが「ヒストグラム」です。
ヒストグラムは、データをいくつかの区間(例えば「0点〜10点」「11点〜20点」…)に分け、各区間に何人いるのかを棒グラフで示したものです。
※ヒストグラムについて詳しくは、こちらのヒストグラムとは?作り方や見方をわかりやすく解説もご覧ください。
もしテストの受験者数が非常に多く、難易度も適切であれば、このヒストグラムの形は正規分布の「山の形」に近くなります。平均点のあたりに多くの生徒が集まり、高得点や低得点の生徒は少なくなるはずです。
しかし、実際のテストでは、以下のような特徴的な形になることもあります。
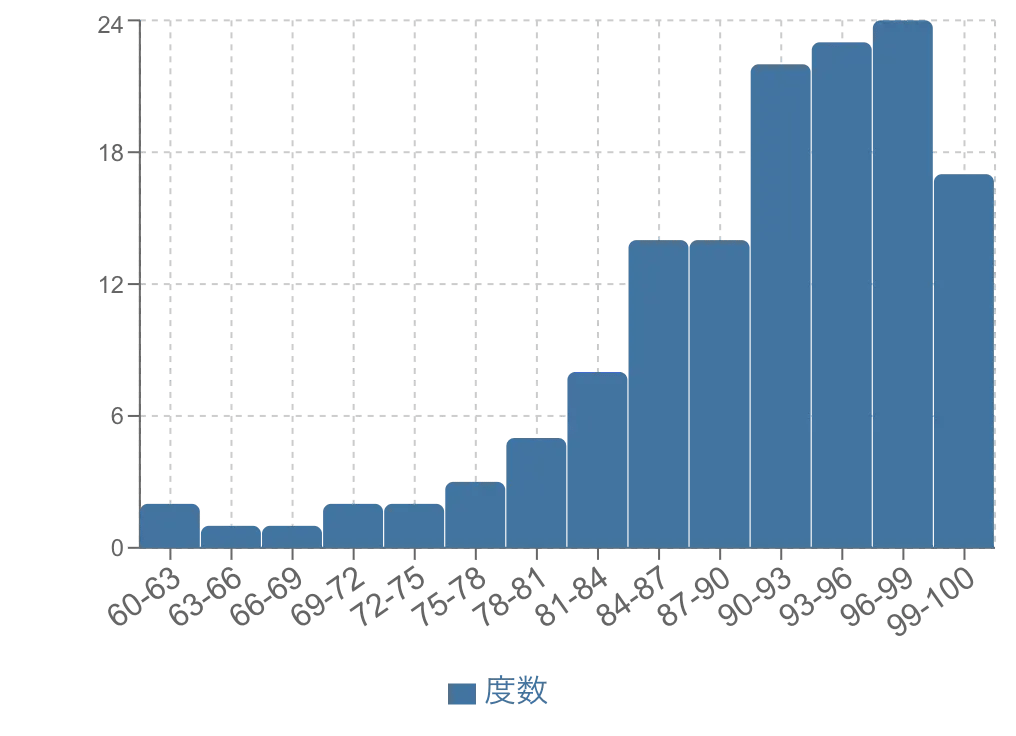
簡単なテストの場合:高得点側に山が偏る。
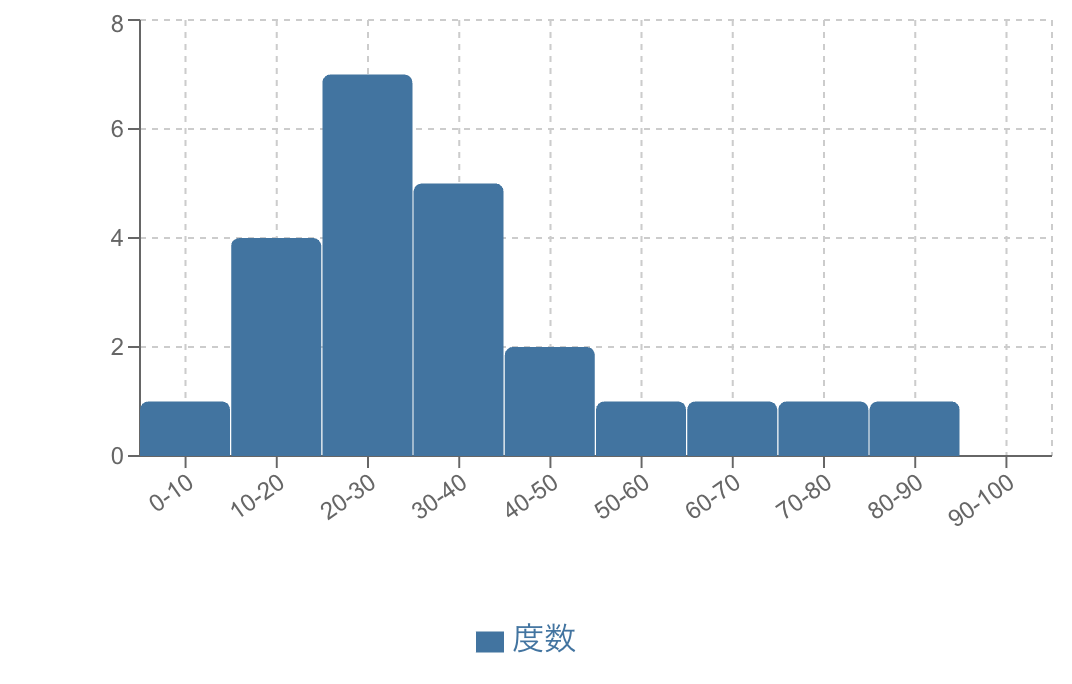
難しいテストの場合:低得点側に山が偏る。
理解度に差がある場合:山が2つできる(二極化)。
.webp)
自分の子供のクラスや、自分が受けたテストの素点データをヒストグラムにしてみると、「平均点」や「偏差値」だけでは見えてこなかった集団の傾向がわかります。
なぜ偏差値のグラフ(正規分布)は「山の形」になるのか?
そもそも、なぜテストの点数や偏差値の分布は、平均点を中心とした「山の形」になる傾向があるのでしょうか?
これは統計学で「中心極限定理(ちゅうしんきょくげんていり)」と呼ばれる原理と関係しています。
難しく聞こえるかもしれませんが、簡単に言えば「世の中の多くの事象は、たくさんの偶然が重なり合った結果、平均値の周りに集まる」という性質です。
テストの点数も同様です。
基礎問題が解けて、応用問題もいくつか正解する「平均的な」点数を取る人が最も多くなります。
すべての問題を完璧に解ける人や、逆にほとんどの問題が解けない人は少数派です。
そのため、多くの人が参加する試験では、自然と「平均点付近に人が集まる、なめらかな山の形」の分布(=正規分布)に近くなるのです。偏差値は、この正規分布を前提として「自分の位置」を示すために作られた指標です。
【実践】データの分布を「ヒストグラム」で作成する方法
では、実際にテスト結果などのデータ分布をグラフ(ヒストグラム)にするにはどうすればよいでしょうか。
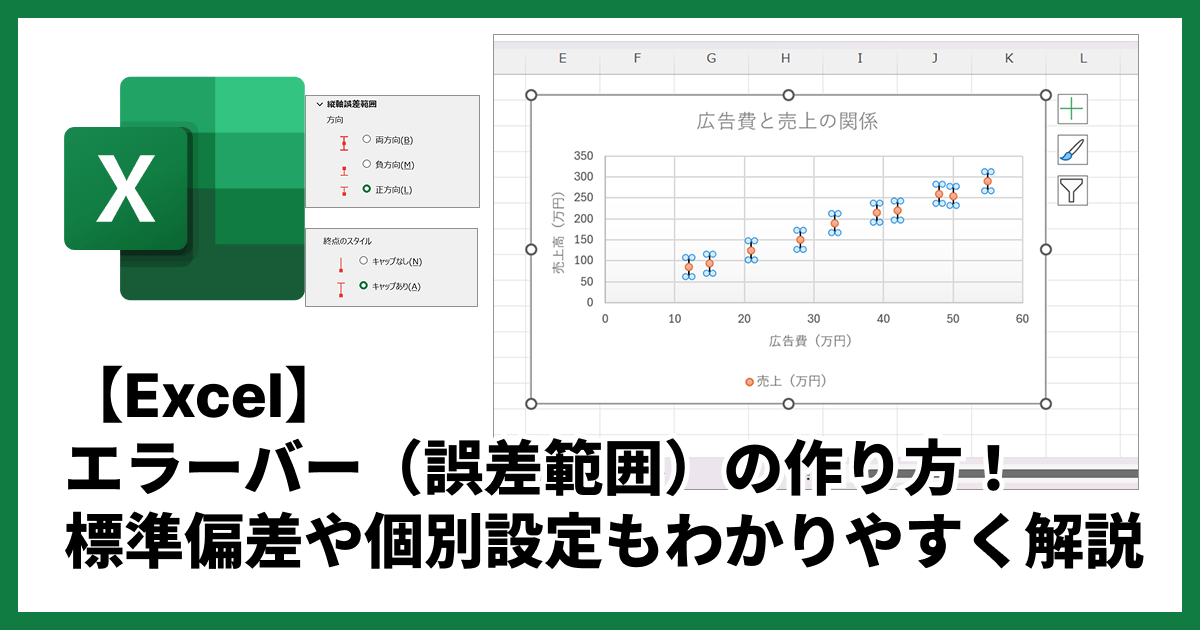
1. ExcelやGoogleスプレッドシートで作成する
ExcelやGoogleスプレッドシートにも、ヒストグラムを作成する機能が標準で備わっています。使い慣れたツールで作成したい場合は、以下の記事で詳しい手順を解説しています。
2. オンラインツールで「ヒストグラム」を簡単に作成する方法
「自分のクラスの点数分布を知りたい」「アンケート結果のばらつきを見たい」といった場合、より手軽にグラフ化できる方法があります。
当サイト「xGrapher」のような無料のオンライングラフ作成ツールを使えば、データを入力(またはコピー&ペースト)するだけですぐにヒストグラムを作成できます。
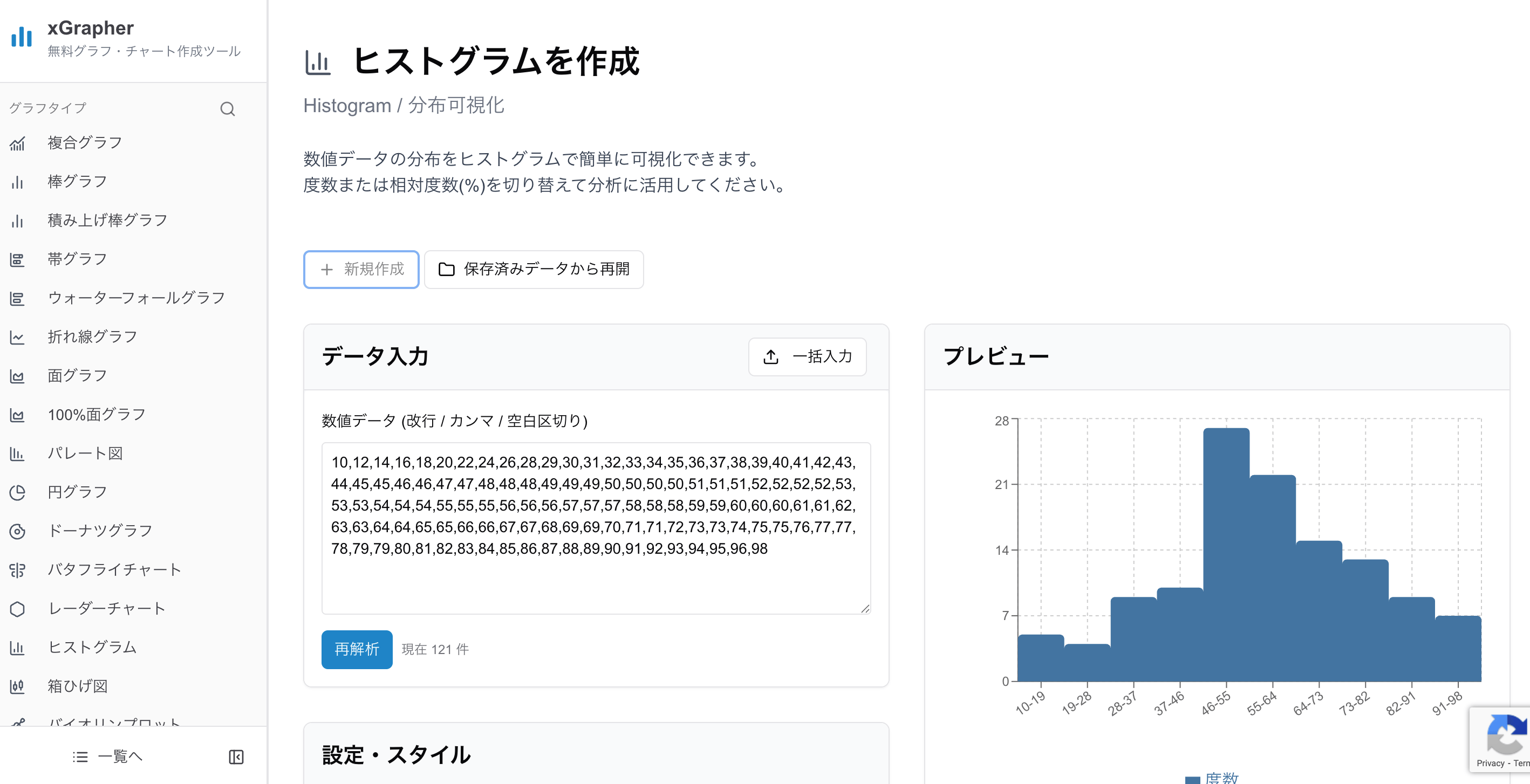
▼ xGrapherでのヒストグラム作成手順
xGrapherのヒストグラム作成ページにアクセスします。
「データ」タブの入力欄に、テストの点数や集計したい数値データを貼り付けます。
グラフの区間(ビンの数)や色、タイトルなどを調整します。
これだけで、データの分布を示すヒストグラムが自動で完成します。
Excelやスプレッドシートを立ち上げる手間もなく、Webブラウザだけですぐに結果を視覚化できるのが大きなメリットです。
まとめ:偏差値のグラフ化で「自分の位置」を客観的に把握しよう
偏差値やテストの結果を「グラフ」にすることで、数字だけではわからなかった多くの情報が見えてきます。
正規分布は、偏差値50を中心とした理想的な集団の姿を示します。
ヒストグラムは、実際のデータがどのようにばらついているか(偏りや二極化など)を明らかにします。
これらのグラフを理解することで、「偏差値60」が全体の中でどの程度の位置なのか、あるいは「今回のテストは高得点に偏っていた」といった集団の特性を、客観的に把握することができます。
ぜひxGrapherのようなツールも活用して、データの可視化を試してみてください。
偏差値とグラフに関するQ&A
Q1. 偏差値の計算式を教えてください。
A1. 偏差値は (自分の得点 - 平均点) ÷ 標準偏差 × 10 + 50 という式で計算されます。「標準偏差」とは、点数のばらつき具合を示す数値です。
Q2. ヒストグラムと棒グラフの違いは何ですか?
A2. どちらも棒状のグラフですが、目的が異なります。
棒グラフ:クラス別(A組, B組)の平均点など、異なる項目同士を比較するために使います。
ヒストグラム:「点数」という1つの連続したデータを区間に分け、その度数(人数)の分布を見るために使います。詳しくはヒストグラムとは?も参照してください。
Q3. 偏差値80や偏差値20は、グラフで見るとどのあたりですか?
A3. 正規分布のグラフで見ると、偏差値80(または20)は、全体の約99.7%が含まれる範囲(偏差値20〜80)の外側に位置します。これは非常にまれなケース(上位または下位の約0.15%)であり、グラフ上ではほとんど見えないほど裾野の端に位置します。
Q4. 自分の偏差値の推移をグラフにしたい場合は?
A4. 複数のテスト結果の偏差値の推移を見たい場合は、「折れ線グラフ」が最適です。横軸にテストの回数(第1回、第2回…)、縦軸に偏差値を取ることで、成績の上がり下がりを一目で確認できます。
Q5. オンラインツールでヒストグラムを作るのは安全ですか?
A5. xGrapherのような多くのオンラインツールは、入力されたデータをサーバーに保存しない設計になっているので安心です(クライアントサイドでの処理)。ただし、機密性の高い個人情報などを扱う場合は、各ツールのプライバシーポリシーや利用規約を確認することをおすすめします。
)
)
)
)
)
)
)
)
)
)
)