ヒストグラムと箱ひげ図の違いとは?見方・特徴・使い分けを徹底解説
データ分析を行う際、手元にある数値の集まり(データセット)がどのような特徴を持っているかを知ることは非常に重要です。平均値や中央値といった代表的な数値を見るだけでなく、データ全体がどのように散らばっているか、つまり「分布」を理解することが、データから正しい情報を読み取る第一歩となります。
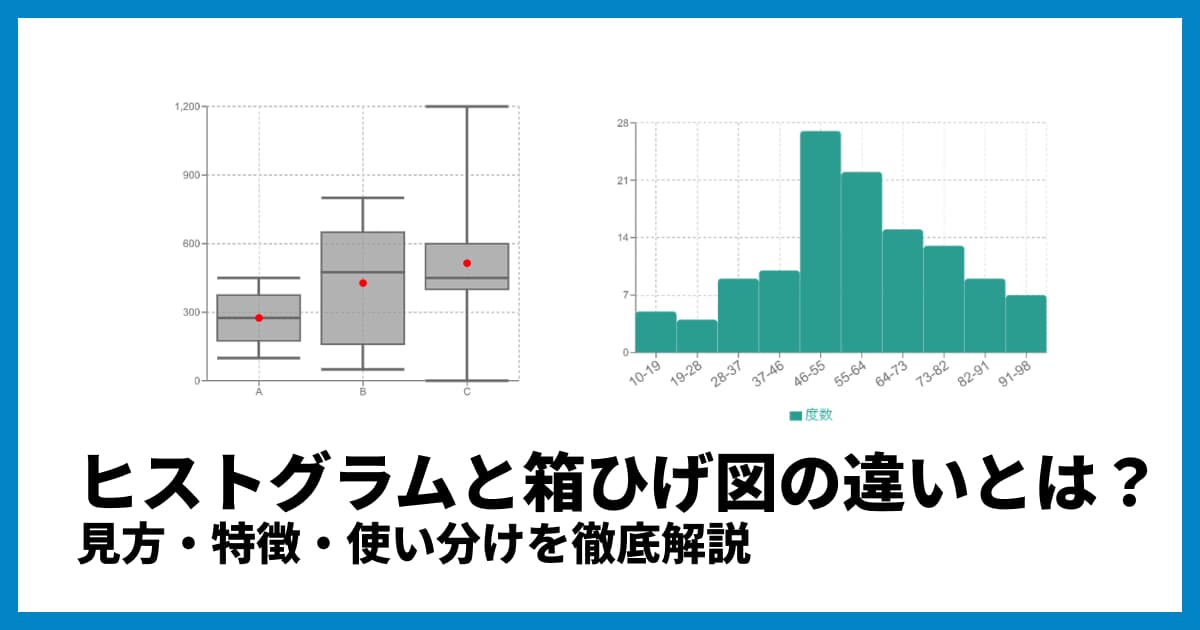
この「データの分布」を視覚的にわかりやすく表現するために使われる代表的なグラフが、「ヒストグラム」と「箱ひげ図」です。
どちらもデータの散らばり具合を見るためのグラフですが、それぞれに異なる特徴があり、得意なこと・不得意なことがあります。「ヒストグラムと箱ひげ図、名前は聞くけど違いがよくわからない」「どちらをいつ使えばいいの?」と迷う方も多いのではないでしょうか。
この記事では、ヒストグラムと箱ひげ図のそれぞれの見方や特徴、明確な違い、そしてシーン別の使い分けについて、わかりやすく解説していきます。
この記事の内容(目次)
ヒストグラムとは? ~データの全体像を掴む~
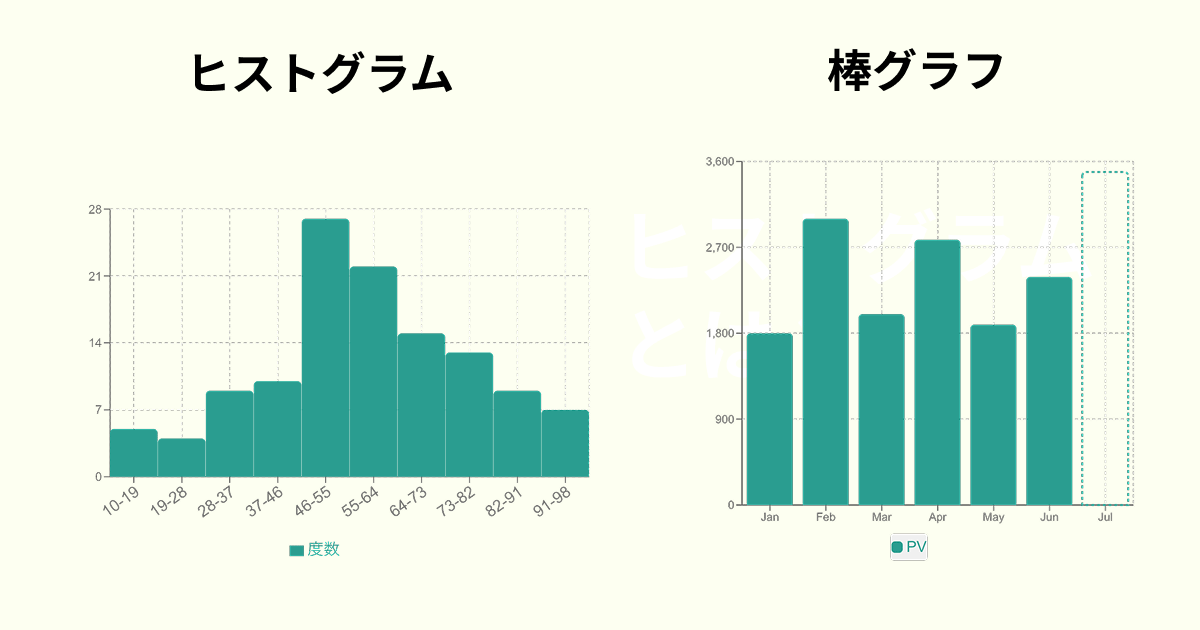
ヒストグラムは、連続する数値データ(例えば、身長、体重、テストの点数、気温など)を一定の「区間(ビンまたは階級)」に区切り、各区間に含まれるデータの個数(度数)を棒グラフのように示したグラフです。
.png)
ヒストグラムの見方
ヒストグラムを見る際は、以下の点に注目します。
山の位置(中心): データの多くがどのあたりに集まっているか。
山の形(分布の形状):
対称か: 左右対称のきれいな山型(正規分布など)か。
歪み(わいど): 左右どちらかに裾が長く伸びていないか。(例: 右に裾が長い=高得点層が少数いる)
山の数: 山は一つか(単峰性)、二つ以上か(二峰性など)。(例: テストの点数で山が二つあれば、得意な層と苦手な層に分かれている可能性がある)
メリットとデメリット
メリット: データの全体的な分布の「形」を視覚的に詳細に把握できます。データがどこに集中し、どのように散らばっているかが一目瞭然です。
デメリット: 区間(ビン)の幅の決め方によって、グラフの見た目が大きく変わってしまいます。また、データの中に極端に離れた値(外れ値)があっても、他のデータに埋もれて分かりにくい場合があります。
ヒストグラムのより詳しい解説や作成方法については、こちらの記事も参考にしてください。
関連記事: ヒストグラムとは?見方や作り方をわかりやすく解説
箱ひげ図とは? ~データのばらつきと外れ値を見る~
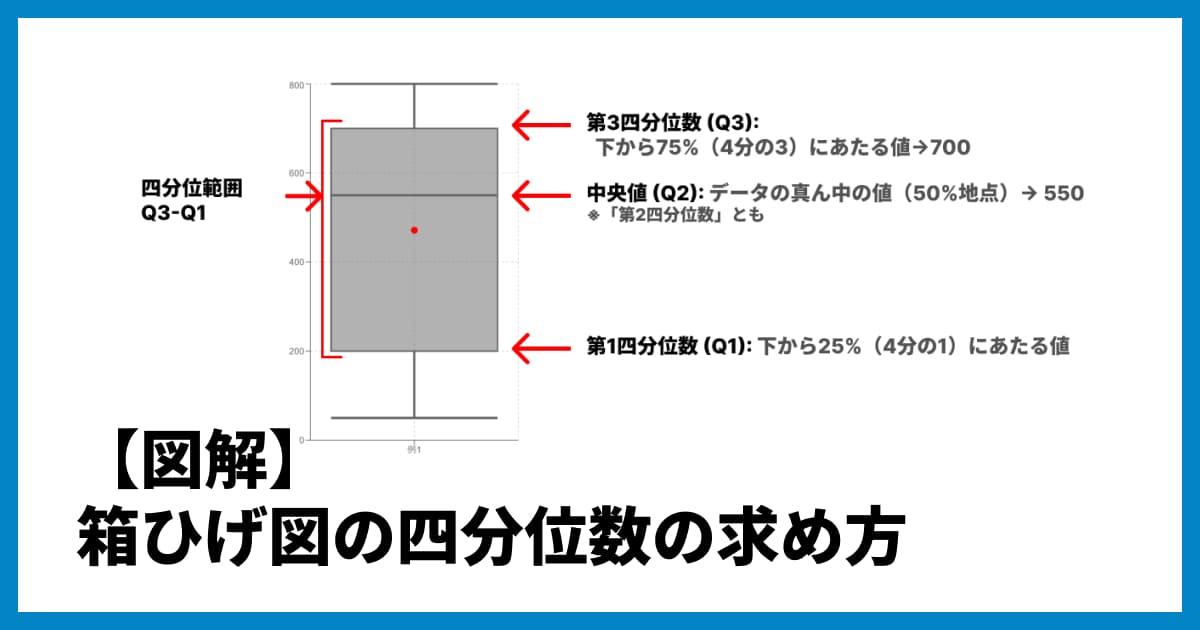
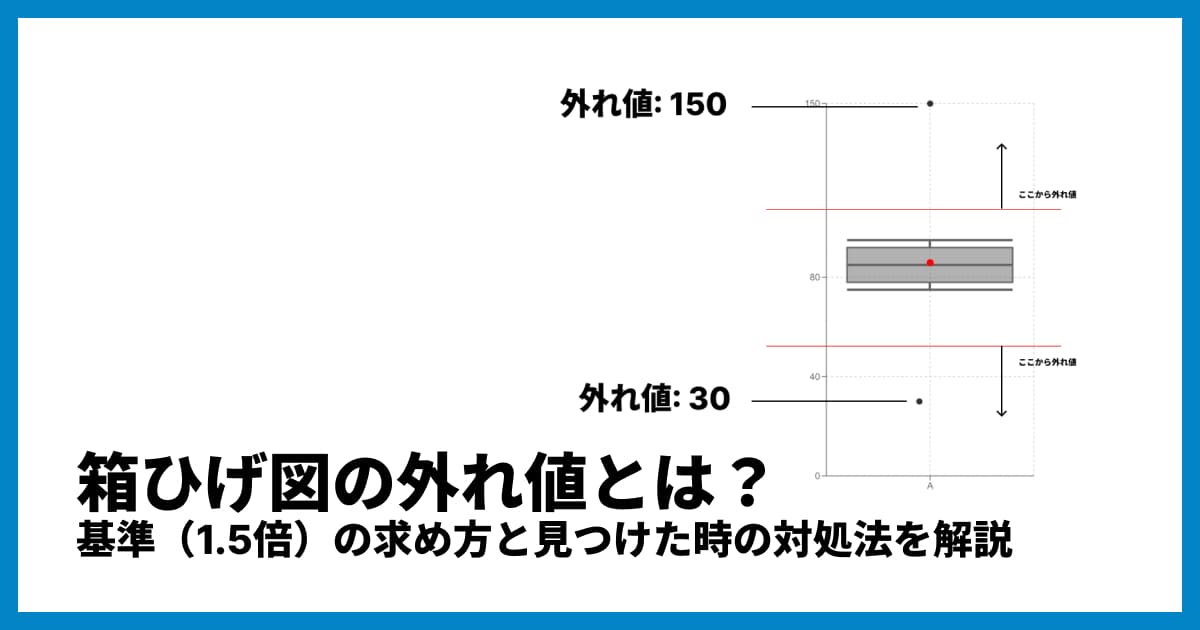
箱ひげ図は、データのばらつきを「五数要約」と呼ばれる5つの数値(最小値、第1四分位数(Q1)、中央値(Q2)、第3四分位数(Q3)、最大値)と「外れ値」を使って表現するグラフです。
.png)
箱ひげ図の見方
箱ひげ図は、以下の5つの主要な要素で構成されています。
中央値 (Q2): データを小さい順に並べたとき、ちょうど真ん中にくる値。データの中心を示します。
箱 (Q1〜Q3): データ全体の中央50%(第1四分位数から第3四分位数まで)が含まれる範囲。この箱が短いほど、データが中央に集中していることを意味します。
ひげ: 箱から上下(または左右)に伸びる線。データの全体の散らばり具合を示します。(※外れ値を除いた最小値・最大値まで伸びることが多いです)
外れ値: 他のデータ群から極端に離れた値。点(プロット)で示されます。
>> 箱ひげ図の「外れ値」の判定方法やその背景
メリットとデメリット
メリット: データの中心傾向(中央値)、ばらつき(箱とひげの長さ)、外れ値の有無を、非常にコンパクトに要約して表現できます。
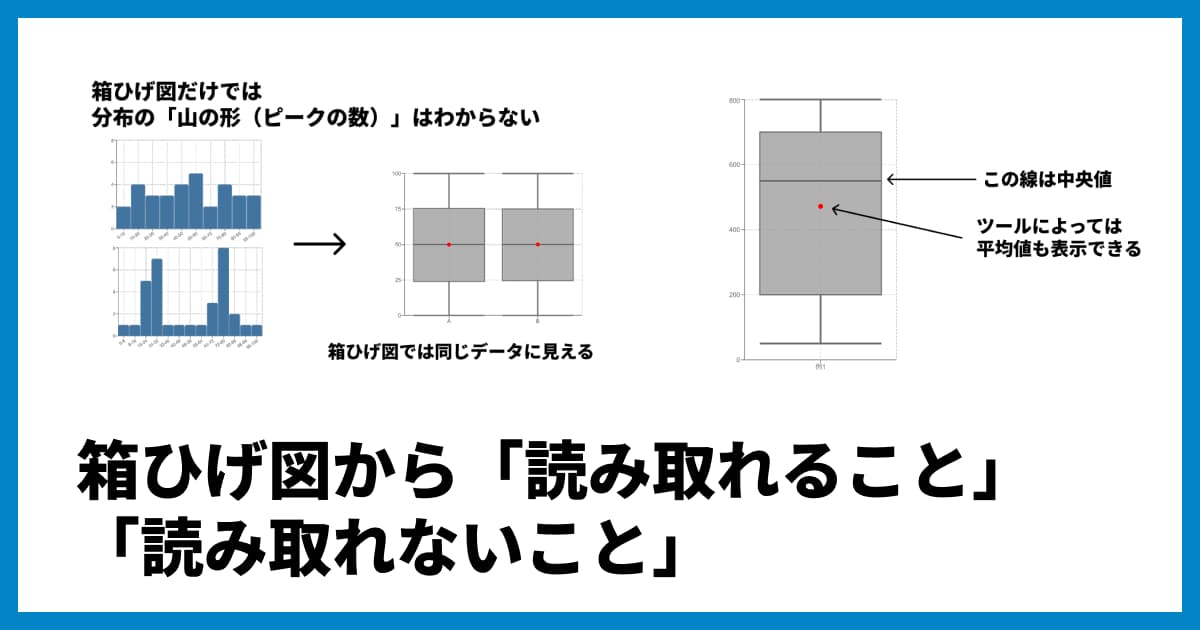
デメリット: 情報を要約しているため、ヒストグラムでわかるような「山の形」や「山の数」といった詳細な分布の形状は分かりません。
箱ひげ図は、特にこの記事の中心テーマの一つでもあり、データの比較に非常に有効です。より詳しい見方や活用法については、以下の記事で詳細に解説しています。
徹底比較!ヒストグラムと箱ひげ図の違い
ヒストグラムと箱ひげ図は、どちらも「データの分布」を見ますが、得意分野が異なります。両者の違いを整理してみましょう。
[画像挿入指示: ヒストグラムと箱ひげ図の比較表(項目:主な目的、わかること、わかりにくいこと、データの要約度、外れ値の検出)]
比較項目 | ヒストグラム | 箱ひげ図 |
|---|---|---|
主な目的 | データの分布の「形状」を詳細に見る | データの「中心・ばらつき・外れ値」を要約して見る |
わかること | ・山の形(対称か、歪んでいるか) | ・中央値(データの中心) |
わかりにくいこと | ・正確な中央値や四分位数 | ・分布の詳細な形状(山の数など) |
データの要約度 | 低い(元データに近い情報量) | 高い(五数要約に集約) |
簡単に言えば、ヒストグラムは「分布の形」を詳細に見るための虫眼鏡、箱ひげ図は「分布の概要(特にばらつき)」を素早く掴むための要約、とイメージするとわかりやすいでしょう。
どっちを使う?シーン別の使い分けガイド
では、実際にデータ分析を行う際、どちらのグラフを使えばよいのでしょうか。目的別の使い分け例を紹介します。
ヒストグラムが適している場合 📊
データ全体の「形」を詳しく知りたいとき
例: 「クラスのテストの点数は、平均点付近に集中しているか?それとも高得点層と低得点層に分かれている(山が二つある)か?」
データの偏り(歪み)を視覚的に確認したいとき
例: 「商品の販売個数は、ほとんどが少数で、時々(右に裾が長く)大口の注文がある、という分布になっていないか?」
一つのデータセットの分布をじっくり観察したいとき
箱ひげ図が適している場合 🧐
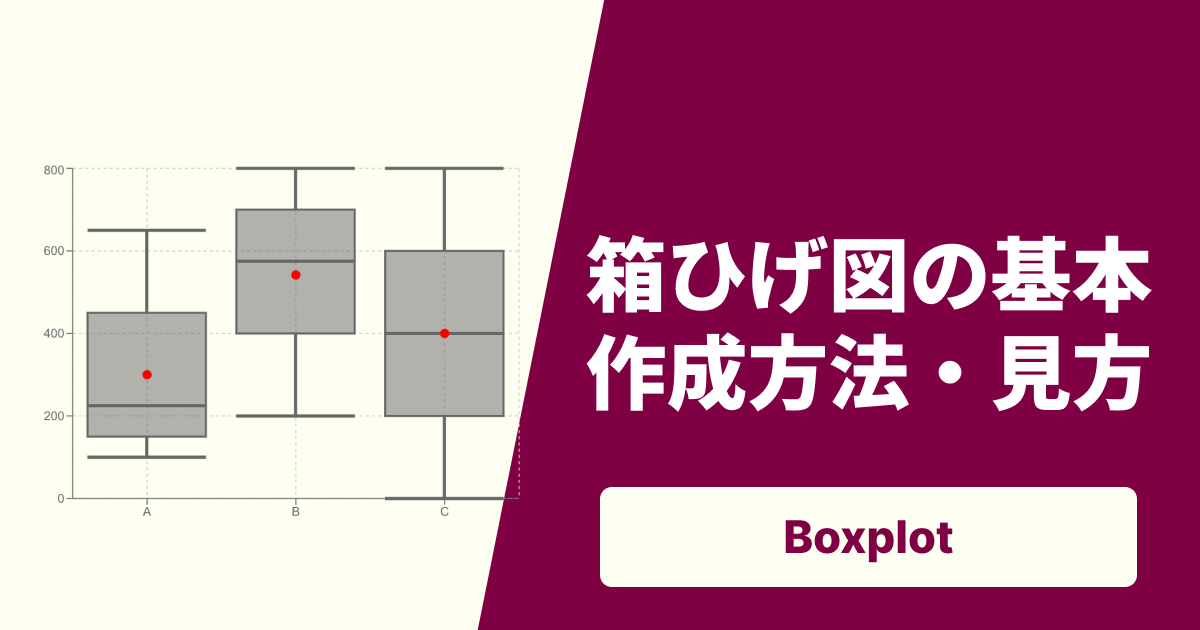
複数のグループのデータを比較したいとき
例: 「A組、B組、C組で、テストの点数のばらつきや中央値に違いはあるか?」
箱ひげ図は縦(または横)に並べて比較するのが非常に得意です。
[画像挿入指示: 複数の箱ひげ図(例: A組, B組, C組)を並べて比較しているグラフ]
データの中に「外れ値」がないか素早く確認したいとき
例: 「アンケートの回答時間で、極端に時間がかかっている(または短すぎる)回答はないか?」
データの中心的な傾向とばらつきの範囲をコンパクトに把握したいとき
特に、複数のグループを比較する場合は、ヒストグラムを複数並べると場所を取る上に比較しづらいため、箱ひげ図が圧倒的に便利です。
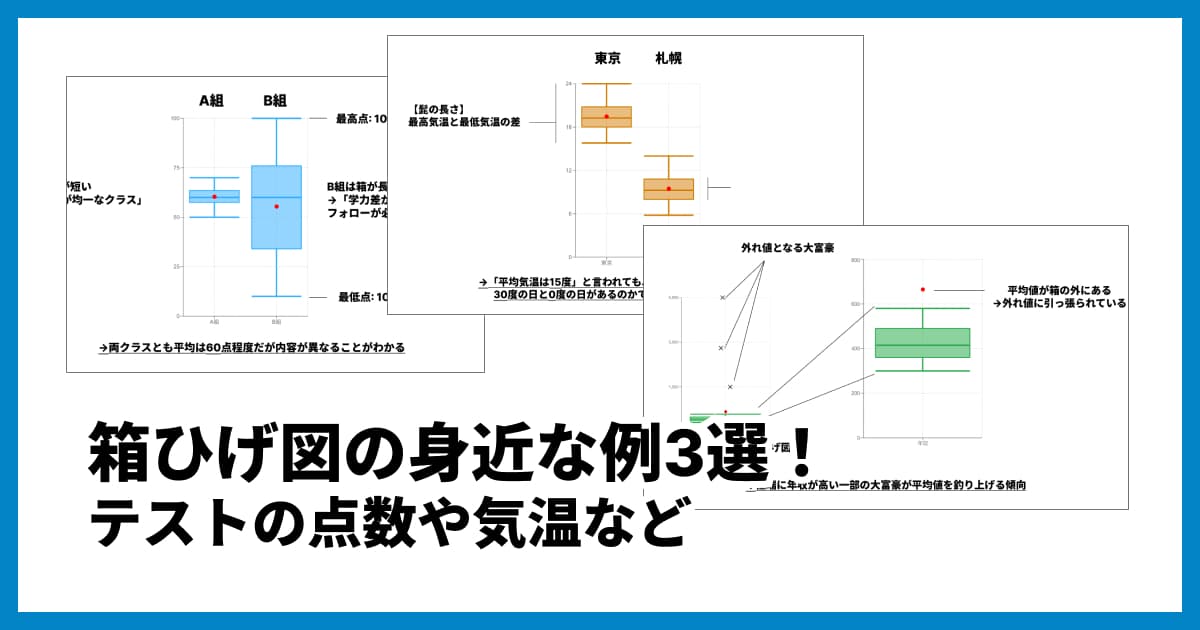
参考記事: 箱ひげ図の身近な例3選!テストの点数や気温など
ヒストグラムと箱ひげ図を組み合わせて使うメリット
「ヒストグラムか、箱ひげ図か」の二者択一ではなく、両方を組み合わせて使うことで、データの理解はさらに深まります。
最も効果的な方法の一つが、同じデータセットから作成したヒストグラムと箱ひげ図を、上下(または左右)に並べて表示することです。
.png)
このように並べることで、以下のようなメリットがあります。
分布の形状と要約を同時に確認できる: ヒストグラムで「山の形(例: やや右に歪んでいるな)」を見つつ、箱ひげ図で「中央値はこのあたりで、データの半分はこの箱の範囲に収まっているな」と、マクロとミクロの視点を同時に得られます。
外れ値の特定が容易になる: 箱ひげ図で検出された「外れ値」が、ヒストグラム上ではどの位置にあるのか(分布の裾のどのあたりか)を具体的に確認できます。
箱ひげ図の弱点を補える: 例えば、箱ひげ図だけでは同じように見えても、元のヒストグラムを見ると一方は山が一つ、もう一方は山が二つ(二峰性)だった、という重要な違いを見逃さずに済みます。
xGrapherでヒストグラム・箱ひげ図を簡単に作成しよう
ヒストグラムや箱ひげ図は、データの分布を理解するために非常に強力なツールですが、いざ作成しようとすると「Excelでの作り方がわからない」「設定が面倒」と感じることもあるかもしれません。
オンライングラフ作成ツールの xGrapher なら、専門的な知識や複雑な操作は不要です。
データをコピー&ペーストするだけ: お手持ちのデータをコピーして貼り付けるだけで、すぐにヒストグラムや箱ひげ図を自動で生成します。
直感的な操作: グラフの種類を切り替えたり、見た目を調整したりするのも簡単です。
Web上で完結: ソフトウェアのインストールは不要。ブラウザさえあれば、誰でもすぐにデータ分析を始められます。
ヒストグラムで分布の形を確認したり、箱ひげ図でグループ間の比較をしたり。これまで解説してきたデータ分析を、xGrapherで今すぐ体験してみませんか?
ヒストグラムを今すぐ作成してみる:
https://xgrapher.com/charts/histogram箱ひげ図を今すぐ作成してみる:
https://xgrapher.com/charts/boxplot
まとめ
今回は、データの分布を視覚化する「ヒストグラム」と「箱ひげ図」について、その違いと使い分けを解説しました。
ヒストグラムは、データの「分布の形状(山の形や数)」を詳細に把握するのに適しています。
箱ひげ図は、データの「中心・ばらつき・外れ値」を要約し、特に複数グループの比較に優れています。
どちらか一方だけを使うのではなく、両方の特徴を理解し、目的に応じて使い分けたり、組み合わせて使用したりすることで、データが持つ情報をより深く、正確に読み解くことができます。
データ分析の第一歩として、ぜひヒストグラムと箱ひげ図を活用してみてください。
ヒストグラムと箱ひげ図に関するQ&A
Q1: ヒストグラムと棒グラフの違いは何ですか?
A1: ヒストグラムは、身長や点数といった連続する一つの量的データを区間(ビン)に区切って、その区間内の度数(個数)を示します。そのため、横軸は連続した数値の区間であり、棒同士はくっつきます。
一方、棒グラフは、クラス別、商品別、地域別といったカテゴリ(質的データ)ごとの量(合計値や平均値など)を比較するために使います。横軸は独立した項目であり、棒同士は離れています。
Q2: 箱ひげ図の「箱」が短い(または長い)場合、どう解釈すればよいですか?
A2: 「箱」は、データ全体の中央50%(Q1からQ3まで)が収まる範囲を示しています。
箱が短い場合: データの中央50%が狭い範囲に密集している、つまり「ばらつきが小さい」ことを意味します。
箱が長い場合: データの中央50%が広い範囲に散らばっている、つまり「ばらつきが大きい」ことを意味します。
.png)
Q3: ヒストグラムの「区間(ビン)の幅」はどうやって決めたらいいですか?
A3: ビンの幅には唯一の正解はありませんが、重要なポイントです。
幅が広すぎると、分布の細かい特徴が潰れてしまい、大雑把な形しかわかりません。
幅が狭すぎると、グラフがギザギザになりすぎて、全体の傾向が掴みにくくなります。
xGrapherのようなツールでは、データの個数や範囲に応じて適切なビンの幅を自動で設定する機能(スタージェスの公式などが使われることが多いです)が備わっていますが、目的に応じて調整してみることも大切です。
Q4: 複数のデータを比較したい場合、ヒストグラムと箱ひげ図のどちらが適していますか?
A4: 箱ひげ図が適しています。箱ひげ図は非常にコンパクトなため、複数のグループのグラフを縦や横に並べても場所を取らず、中央値の位置、ばらつき(箱の長さ)、外れ値の有無などを一目で比較できます。ヒストグラムを並べると、分布の形状の違いはわかりますが、場所を取るため比較しにくくなります。
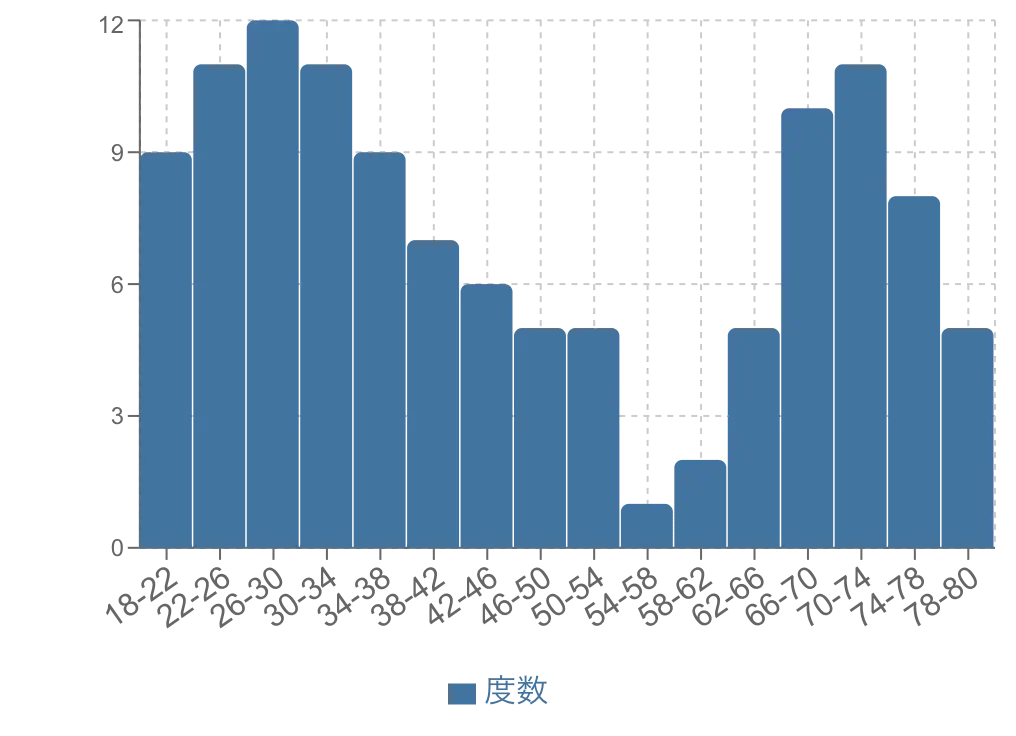
Q5: 箱ひげ図ではわからない「山の数(二峰性など)」は、なぜ重要なのでしょうか?
A5: 例えば、あるクラスのテストの点数で、平均点は50点だったとします。箱ひげ図だけ見ると、中央値が50点付近にある普通の分布に見えるかもしれません。しかし、ヒストグラムで確認したところ、実際には「30点付近の層」と「80点付近の層」の二つの山(二峰性)に分かれていた、という可能性があります。これは「平均点付近の生徒はほとんどいない」という重要な事実を示しており、箱ひげ図だけでは見落としてしまう可能性があります。
)
)
)
)
)
)
)
)
)
)
)