箱ひげ図の外れ値とは？基準（1.5倍）の求め方と見つけた時の対処法を解説

外れ値の基準は？「IQRの1.5倍」ルールを分かりやすく解説

箱ひげ図の外れ値は、感覚で「外れている」と決めているわけではなく、「四分位範囲（IQR: Interquartile Range）」に基づいた明確な計算ルールによって定義されています。

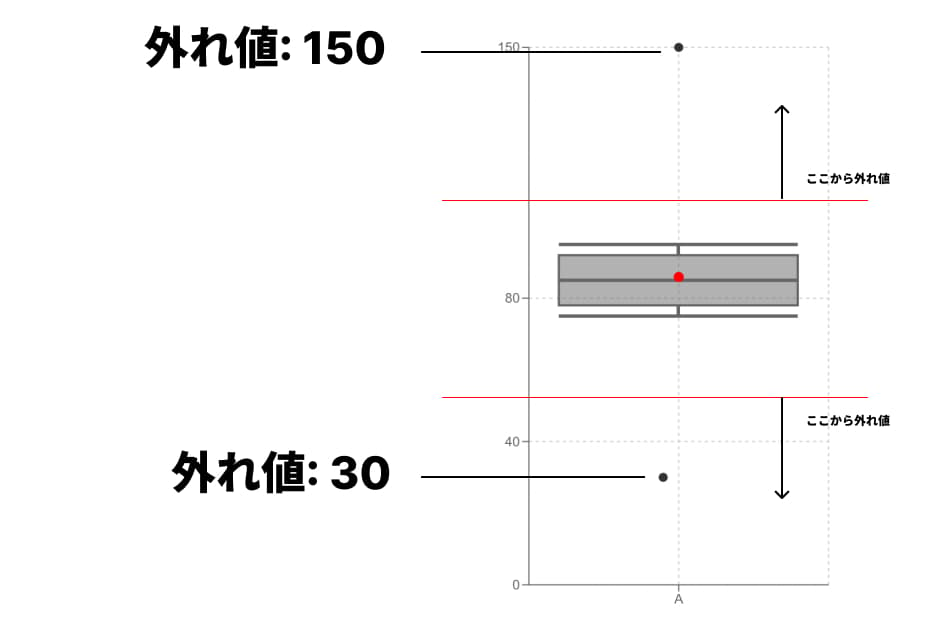
この計算方法を、具体的なデータセット([ 82, 75, 88, 92, 30, 85, 150, 78, 95, 90, 80 ])と共に見ていきましょう。

1. データを並び替える: まず、データを小さい順に並べます。

   1. [ 30, 75, 78, 80, 82, 85, 88, 90, 92, 95, 150 ]

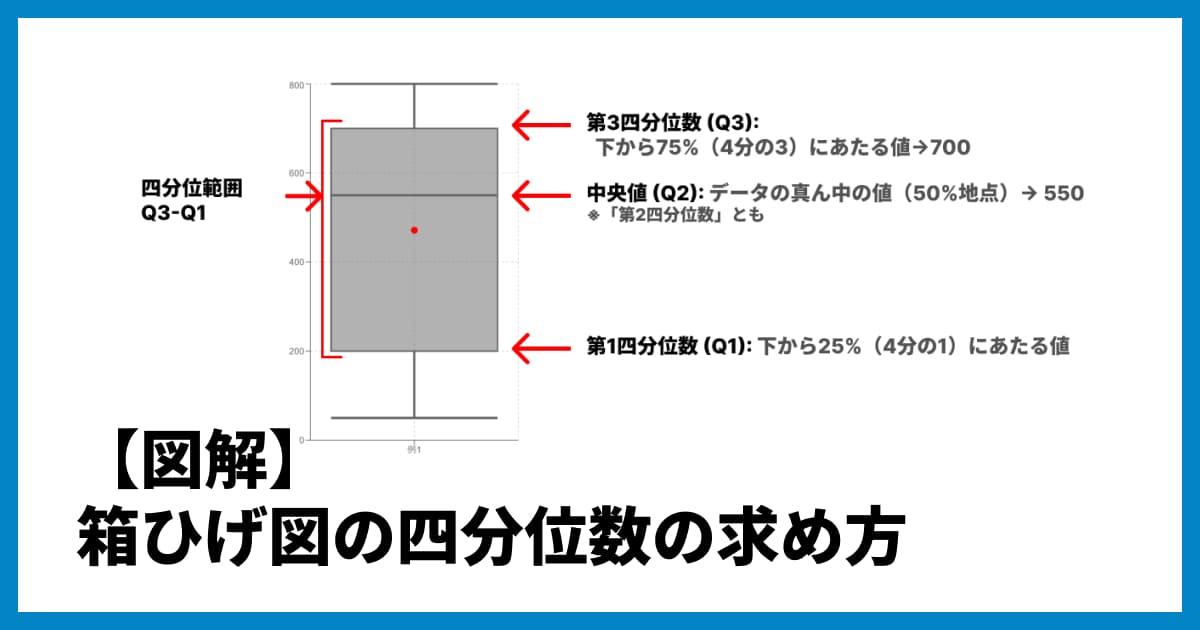
2. 四分位数を探す: データを4等分する位置にある値を探します。

   • 第1四分位数 (Q1): 全体の下から25%の位置にある値。
     →下位半分（1〜5番目）の真ん中（3番目）の値: 78

   • 中央値 (Q2): 全体の50%の位置にある値。
     →11個の真ん中（6番目）の値: 85

   • 第3四分位数 (Q3): 全体の下から75%の位置にある値。（ちなみに中央値は第2四分位数(Q2)です）
     →上位半分（7〜11番目）の真ん中（9番目）の値: 92

3. 四分位範囲 (IQR) を計算する: 第3四分位数から第1四分位数を引きます。これがデータの「真ん中50%」の範囲を示します。

   • $IQR = Q3 - Q1$
     →Q3 - Q1 = 92 - 78 = 14

この IQR を使って、外れ値の境界線（「ひげ」の上限・下限の最大範囲）を計算します。

• 外れ値の上限: $Q3 + (1.5 \times IQR)$
  → 92 + 21 = 113

• 外れ値の下限: $Q1 - (1.5 \times IQR)$
  → 78 - 21 = 57

つまり、この「$Q3 + (1.5 \times IQR)$」の値よりも大きいデータ(150)、または「$Q1 - (1.5 \times IQR)$」の値よりも小さいデータ(30)が、「外れ値」として扱われ、グラフ上では点（プロット）で示されるのです。

この場合、グラフ上の「ひげ」の上端は、境界線(113)の内側にある最も遠いデータ点、つまり「95」まで引かれます。ひげの下端は、境界線(57)の内側にある最も遠いデータ点、つまり「75」まで引かれます。

なぜ「1.5倍」？ 正規分布との関係

この「1.5倍」という係数は、統計学者のジョン・テューキー（John Wilder Tukey）が提唱した経験則です。

データの分布が「正規分布」というきれいな釣鐘型に従う場合、平均値から標準偏差（σ）の $\pm 2\sigma$の範囲に約 95.4% のデータが入ることが知られています。

[正規分布のヒストグラム]

箱ひげ図は平均値や標準偏差ではなく、中央値や四分位点を基準にしていますが、この「$1.5 \times IQR$」ルールは、正規分布における$\pm 2.7\sigma$程度に相当するように設計されています。 これにより、両側のひげを伸ばしても全体の約99.3%前後が範囲内に入るようになります。つまり、外れ値として検出されるのは全体の約0.7%程度となり、「滅多に起こらないが、注目すべき値」を検出するのに実用上ちょうどよい基準とされているのです。

係数が「3倍」の場合も？（極端な外れ値）

一般的に「1.5倍」が広く使われますが、分析の目的やツールによっては、より厳しい基準である「3倍」ルールが使われることもあります。

• 極端な外れ値の上限: $Q3 + (3 \times IQR)$

• 極端な外れ値の下限: $Q1 - (3 \times IQR)$

この「3倍」の境界線（$Q3 + 3 \times IQR$ や$Q1 - 3 \times IQR$）すらも超える値は、特に注目すべき「極端な外れ値 (Extreme Outlier)」と呼ばれます。 （この場合、$1.5 \times IQR$を超え$3 \times IQR$ 以内の値は「外れ値 (Mild Outlier)」として区別されることもあります）

基本的な見方としては、まずは「1.5倍」のルールを覚えておけば十分です。

箱ひげ図の基本的な見方や四分位数については、こちらの記事でも詳しく解説しています。
箱ひげ図（Boxplot）とは？見方やメリット、作成方法を解説

なぜ外れ値が重要なのか？見逃してはいけない理由

外れ値は、グラフを見にくくする「邪魔者」のように思えるかもしれませんが、実はデータに関する重要な情報を私たちに教えてくれるサインです。

外れ値が発生する主な理由は、大きく分けて3つあります。

1. データ入力のミス

最も単純な理由ですが、見落としがちなのが入力ミスです。

• 例: 年齢「25」を「250」と入力した。

• 例: 売上「10,000」を「1,000」と一桁間違えた。
  このようなあり得ない値や、極端な値は外れ値として検出されやすいため、データのクリーニング（修正）に役立ちます。

2. 測定エラーや特殊な事象

データ収集時の何らかのトラブルや、一時的な特殊要因によって発生することもあります。

• 例: センサーの一時的な故障による異常な測定値。

• 例: WebサイトへのDDoS攻撃による一時的なアクセス急増。

• 例: 大規模セールやキャンペーンによる一時的な売上増加。
  これらは「通常の状態」とは異なるため、外れ値として現れます。

3. データに潜む重要な特徴（インサイト）

これが最も重要です。外れ値は、他の大多数のデータとは異なる、特異な性質を持つグループを示している可能性があります。

• 例: 他の顧客より突出して購入額が多い「優良顧客」。

• 例: 他の製品より極端に不良品率が低い「高品質な生産ライン」。

もし外れ値を「ノイズ」として単純に無視してしまうと、こうした重要な発見の機会を逃してしまうことになります。

データの分布全体を把握するヒストグラムと、外れ値を明確に可視化する箱ひげ図を併用することで、データへの理解がより深まります。

ヒストグラムと箱ひげ図の違いは？使い分けとデータ分布の理解

外れ値を見つけたらどうする？削除する前に確認すべきこと

外れ値を発見したとき、最もやってはいけないのが「分析の邪魔だから」という理由だけで安易に削除することです。

外れ値を見つけたら、以下のステップで冷静に対処しましょう。

Step 1: まずは原因を調査する
その外れ値が、前述した「入力ミス」「特殊な事象」「重要な特徴」のどれに該当するのかを調査します。

• そのデータが発生した日時や担当者、状況を確認します。

• 「200歳」や「マイナスの売上」など、明らかにあり得ない値かどうかを確認します。

Step 2: 原因に応じて対処する

• 原因が「入力ミス」の場合:

  • 可能であれば、正しい値に修正します。

  • 正しい値が不明で、分析に大きな影響を与えると判断される場合は、削除を検討します。ただし、削除した旨を記録しておくことが重要です。

• 原因が「測定エラー」や「特殊な事象」の場合:

  • これは分析の目的によります。

  • 「平常時の傾向」を知りたいのであれば、そのデータを除外して分析することが妥当かもしれません。

  • 一方で、「異常検知」や「セールス効果の測定」が目的ならば、その外れ値こそが最も重要な分析対象となります。

• 原因が「重要な特徴」の場合:

  • 絶対に削除してはいけません。

  • なぜそのデータだけが他と異なるのか（例: なぜその顧客だけが突出しているのか）を深掘りすることで、ビジネス上の重要なヒントが得られる可能性があります。

迷った場合は、「外れ値を含めた分析」と「外れ値を除外した分析」の両方を行い、結果がどのように変わるかを比較するのも有効な手段です。

※ただし後述するようにExcelで箱ひげ図を作成する場合は、「外れ値を含めた分析」には対応していません

オンラインで簡単！箱ひげ図と外れ値を確認する方法

ここまで解説したように、外れ値の計算（四分位数やIQR）は、手作業で行うのはなかなか大変です。

Excel（エクセル）でも箱ひげ図を作成することはできますが、バージョンによっては操作が少し複雑な場合もあります。

>> Excel（エクセル）で箱ひげ図を作成する方法

またExcel（エクセル）では外れ値の判定は必ず入るため、外れ値を含める含めないなどのオプションがありません。

そんな時おすすめなのが「xGrapher」です。インストール不要、無料で使えるオンラインのグラフ作成ツールです。

お手元のデータをコピー＆ペースト（またはCSVファイルをドラッグ＆ドロップ）するだけで、自動で外れ値が計算され、誰でも簡単に美しい箱ひげ図を作成できます。

[外れ値のオプション選択画面]

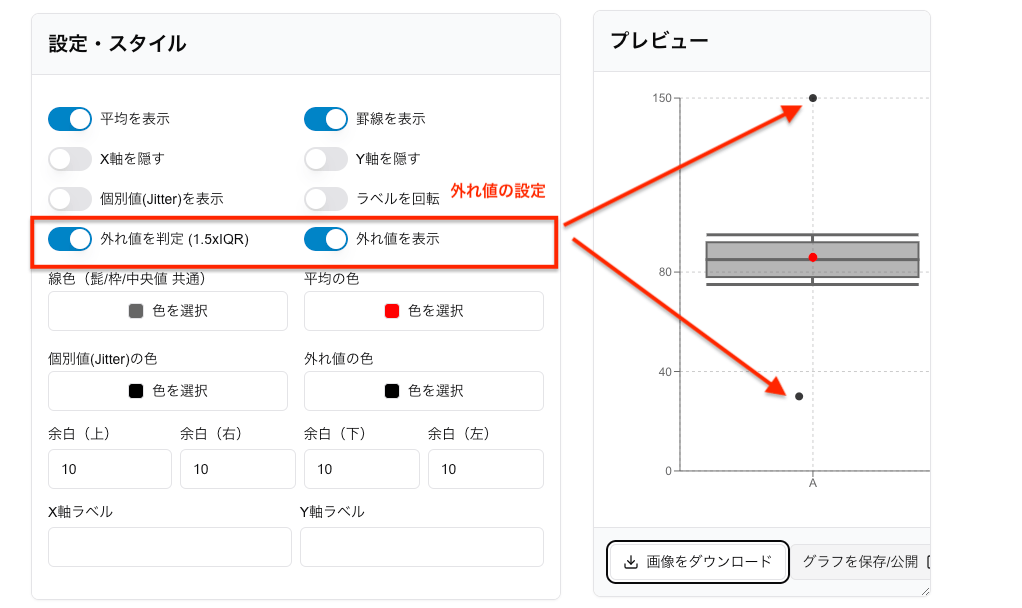
データの分布を確認したり、グループ間の比較をしたりする際に、外れ値がどこにあるかを一目で把握できるので、データ分析の第一歩として非常に便利です。

ぜひ、以下のリンクからxGrapherの箱ひげ図作成機能をお試しください。

無料でオンライン箱ひげ図を作成 - xGrapher

まとめ

箱ひげ図における「外れ値」は、データ分析において非常に重要な情報源です。

• 外れ値は、一般的に「$Q3 + 1.5 \times IQR$」より上、または「$Q1 - 1.5 \times IQR$」より下の値として定義されます。

• 外れ値は、単なるミスである場合もあれば、分析すべき重要な事象や特異なデータを示している場合もあります。

• 外れ値を見つけたら、安易に削除せず、まずその原因を調査することが鉄則です。

• xGrapherのようなオンラインツールを使えば、誰でも簡単に箱ひげ図を作成し、外れ値の有無を視覚的に確認できます。

外れ値を正しく理解し、適切に対処することで、データ分析の質を大きく向上させることができます。

箱ひげ図と外れ値に関するQ&A

Q1: 外れ値は必ず「悪い」データですか？

A1: いいえ、そうとは限りません。入力ミスや測定エラーなど「修正・削除すべきデータ」である場合もありますが、一方で「非常に優秀な成績」や「特異な優良顧客」など、分析上最も重要な「宝物」である可能性もあります。

Q2: 外れ値の基準である「1.5倍」を変更することはできますか？

A2: はい、分析ツールやプログラムによっては変更可能です。例えば、より厳しい基準で外れ値を見たい場合、この倍率を「3倍」に設定することもあります（3倍を超えるものは「極端な外れ値」と呼ばれることがあります）。ただし、一般的には「1.5倍」が広く使われています。

Q3: 外れ値がたくさんある場合、どうすればよいですか？

A3: 外れ値が多数発生する場合、そのデータは正規分布のような左右対称の分布ではなく、特定の方向に裾が長い「歪んだ分布」をしている可能性があります。この場合、対数変換などのデータ変換を行うことで、分布の形を整えて分析しやすくする方法もあります。

Q4: 「ひげ」の長さはどこまでですか？

A4: ひげの端は、Q1やQ3から「$1.5 \times IQR$」の範囲内にある、最も外側のデータ点まで引かれます。外れ値の境界線（$Q1 - 1.5 \times IQR$）そのものではない点に注意が必要です。

Q5: 外れ値と異常値はどう違いますか？

A5: 「外れ値」は、本記事で解説したように統計的な基準（$1.5 \times IQR$ルールなど）に基づいて「分布から外れている」と判断された値です。一方、「異常値」は、そのデータが「あり得ない値（例: 年齢が300歳）」や「測定エラー」など、データの発生経緯として異常であると判断された値というニュアンスで使われることが多いです。外れ値であっても、異常値ではない（例: 突出した売上）こともあります。

Q6: Excelで外れ値の表示・非表示を切り替えるには？

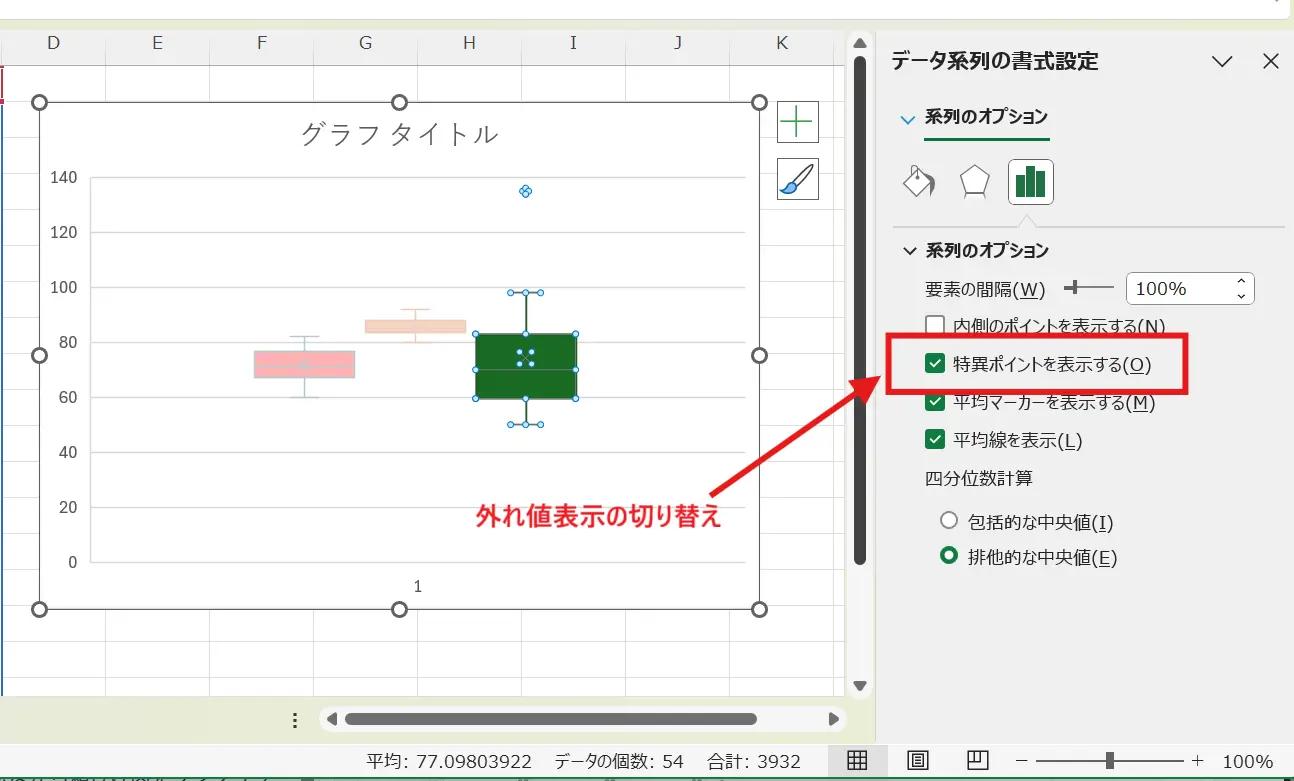
A6: 以下の手順で切り替えが可能です。

1. グラフのいずれかの箱をクリックし、データ系列全体を選択します。

2. 右クリックして「データ系列の書式設定」を選択します。

3. 「系列のオプション」が表示されます

4. 「特異ポイントを表示する」のチェックボックスで、外れ値を点として表示するかどうかを切り替えられます