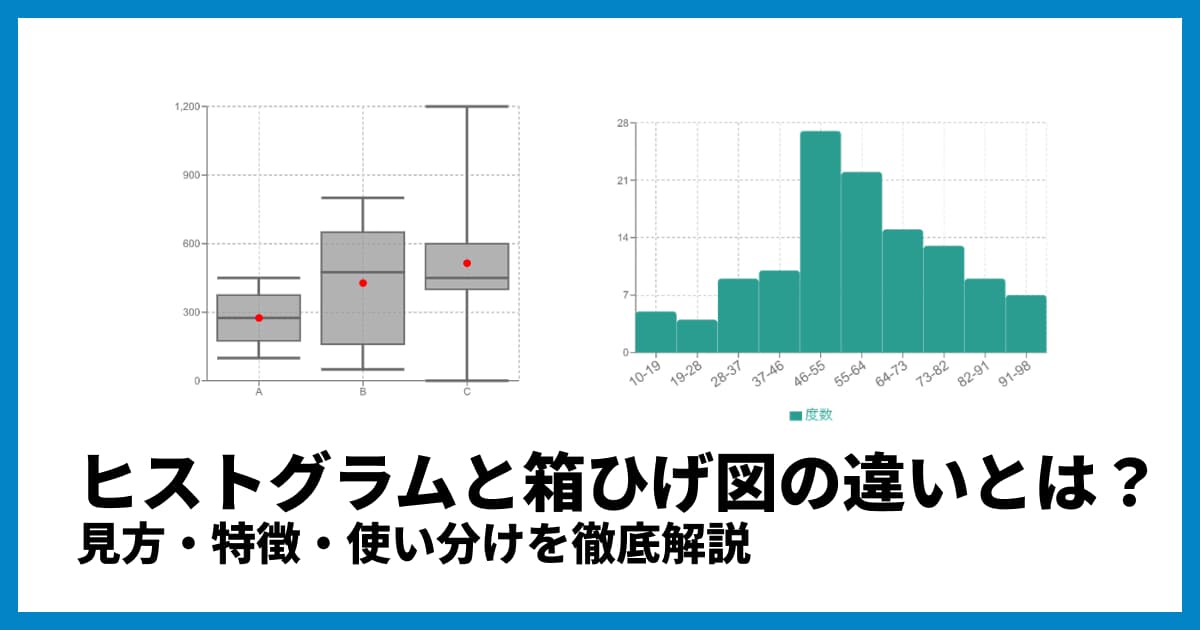
箱ひげ図(ボックスプロット)とは?見方と作り方をわかりやすく解説!
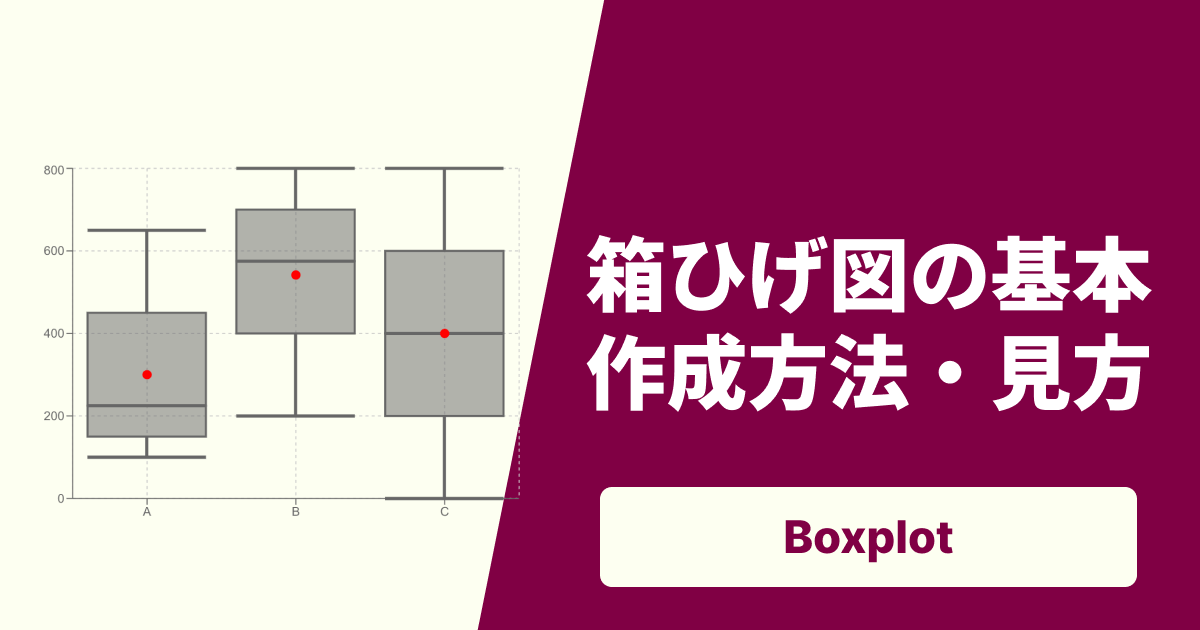
「箱ひげ図(はこひげず)」、または「ボックスプロット(Box Plot)」というグラフを知っていますか? 名前は少し変わっていますが、これは「データのばらつき具合」をひと目で把握するのに非常に便利なグラフです。
例えば、クラスAとクラスBのテストの点数を比較したいとき、平均点だけを比べても「全体がどのくらい散らばっているか」はわかりません。クラスAは全員が70点前後に固まっているかもしれませんが、クラスBは50点の人から100点の人まで幅広く分布しているかもしれません。
箱ひげ図は、そうしたデータの分布の様子を、「箱」と「ひげ」を使ってシンプルに表現してくれます。この記事では、箱ひげ図の基本的な見方から、そのメリット、簡単な作り方まで、わかりやすく解説していきます。
この記事の内容(目次)
箱ひげ図の見方:5つの「線」の意味を理解しよう
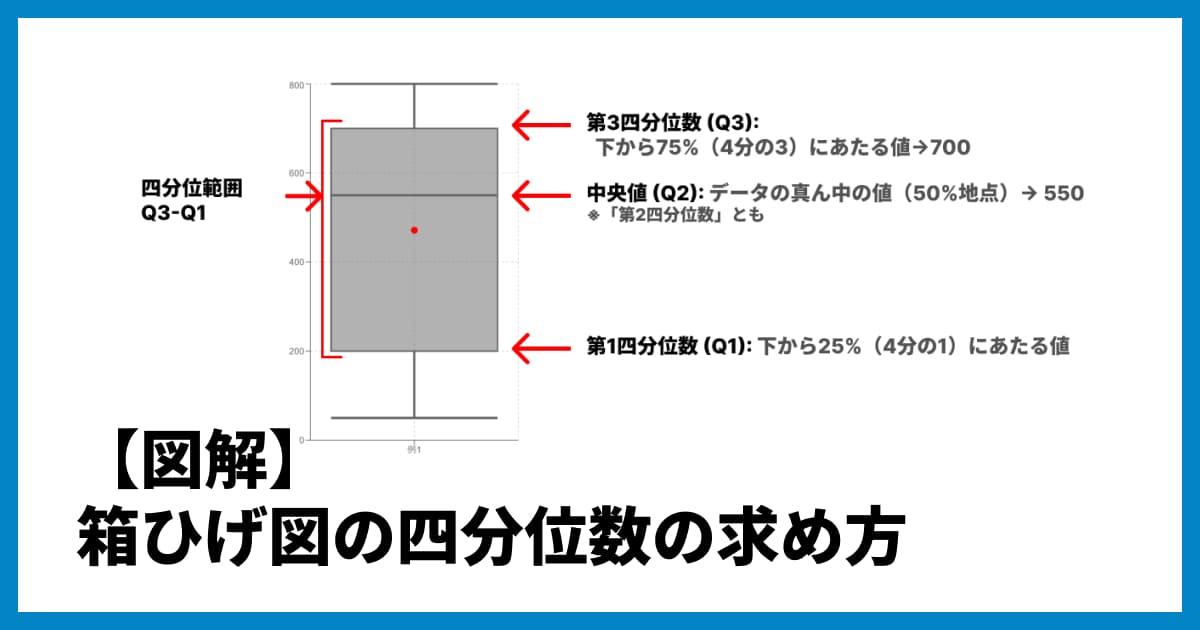
箱ひげ図は、一見すると複雑に見えるかもしれませんが、構成要素はとてもシンプルです。基本的には、データの「最小値」「最大値」、そしてデータを4分割したときの区切りの値である「四分位数(しぶんいすう)」という5つの数値(5数要約とも呼ばれます)で構成されています。
.png)
① 最小値(Minimum): データの最も小さい値。(ただし、後述する「外れ値」を除く場合があります)
② 第1四分位数 (Q1): データを小さい順に並べたとき、下から25%(4分の1)にあたる値。
③ 中央値 (Q2): データの真ん中の値(50%地点)。「第2四分位数」とも呼ばれます。
④ 第3四分位数 (Q3): データを小さい順に並べたとき、下から75%(4分の3)にあたる値。
⑤ 最大値(Maximum): データの最も大きい値。(ただし、「外れ値」を除く場合があります)
そして、グラフの各部分は以下のように呼ばれます。
.png)
箱 (Box): 第1四分位数(Q1)から第3四分位数(Q3)までの範囲。この箱の中に、データ全体の真ん中50%が含まれます。
箱の中の線: 中央値(Q2)を示します。
ひげ (Whisker): 箱の両端から最小値と最大値まで伸びる線。
箱の長さとひげの長さが「ばらつき」を示す
箱ひげ図を見るときに重要なのは、各部分の「長さ」です。
.png)
箱の長さが短い:データの中央50%が狭い範囲に集中している(ばらつきが小さい)。
箱の長さが長い:データの中央50%が広い範囲に散らばっている(ばらつきが大きい)。
ひげが短い/長い:箱の外側(上位25%や下位25%)のデータの散らばり具合を示します。
また、箱の中の「中央値」の線が箱の真ん中からズレている場合、データの分布に偏りがあることがわかります。
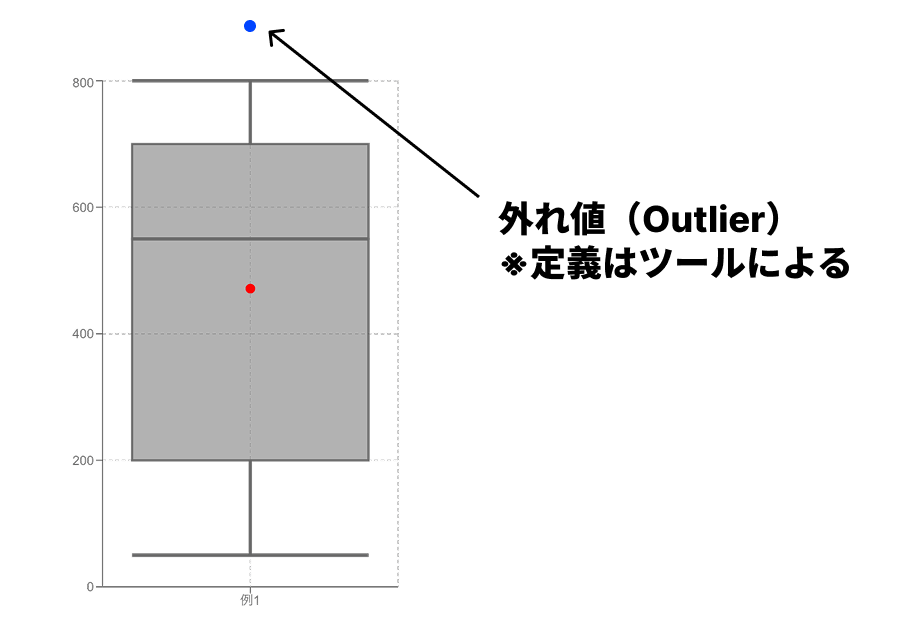
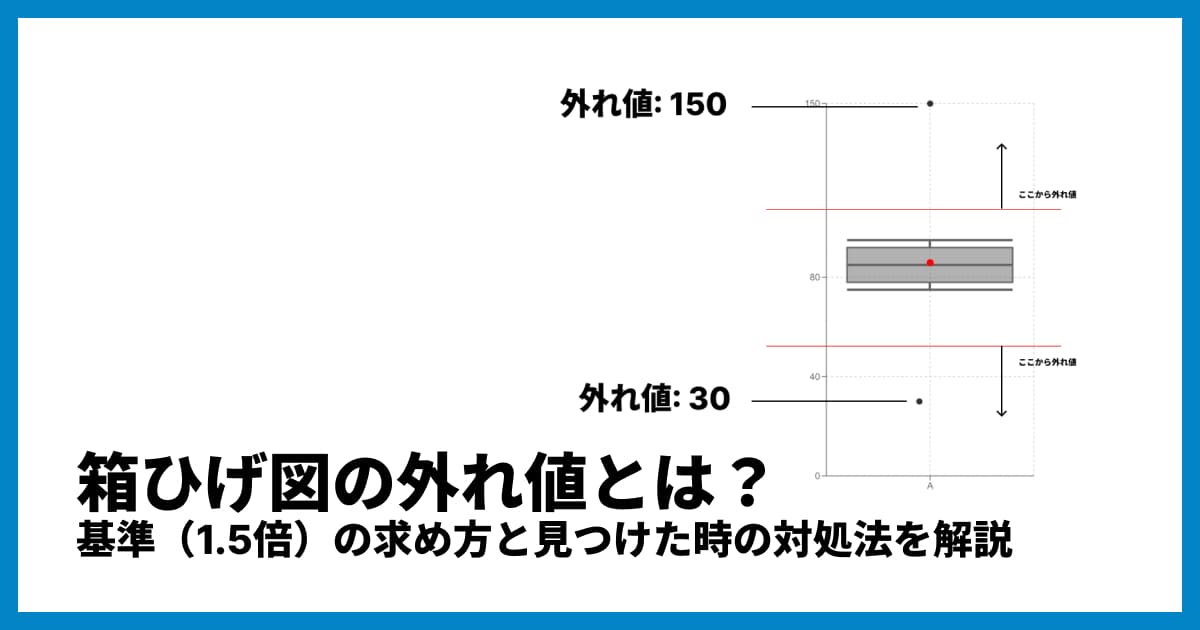
「外れ値」の表示
グラフによっては、ひげのさらに外側に「・」や「×」などの点でデータが表示されることがあります。これは「外れ値(はずれち)」と呼ばれ、他のデータ群から極端に離れた値を示します。
一般的に、箱の長さ(Q3 - Q1、これを四分位範囲(IQR)と呼びます)の1.5倍を超えて離れているデータが外れ値として扱われることが多いです。(※この定義はツールによって異なる場合があります)
参考記事:
箱ひげ図の見方「読み取れること・読み取れないこと」を解説!
【図解】箱ひげ図の四分位数の求め方を徹底解説!データの偶数・奇数やエクセルとの違いとは?
箱ひげ図から何がわかる?メリットと活用シーン
箱ひげ図の基本的な見方がわかったところで、次にこのグラフを使うメリットと、どのような場面で役立つのかを見ていきましょう。
メリット1:データの分布とばらつきが一目瞭然
最大のメリットは、データの散らばり具合(分布)を視覚的に素早く把握できることです。平均値や中央値といった「代表値」だけでは見えてこない、データの全体像を掴むのに役立ちます。
データがどの範囲に広がっているか(最大値と最小値)
データがどこに集中しているか(箱の長さ)
データの中心はどこか(中央値)
データは偏っているか(中央値の位置)
メリット2:複数のグループの比較が簡単
箱ひげ図は、複数のデータグループを並べて比較する際に真価を発揮します。
例えば、複数の店舗の売上データ、異なる製造ラインの製品重量、地域ごとの気温変化などを箱ひげ図で並べると、以下のような点を瞬時に比較できます。
「どのグループが最もばらつきが大きいか?(箱やひげが長いか)」
「どのグループの中央値が最も高いか?」
「Aグループの上位25%は、Bグループの中央値よりも高いか?」
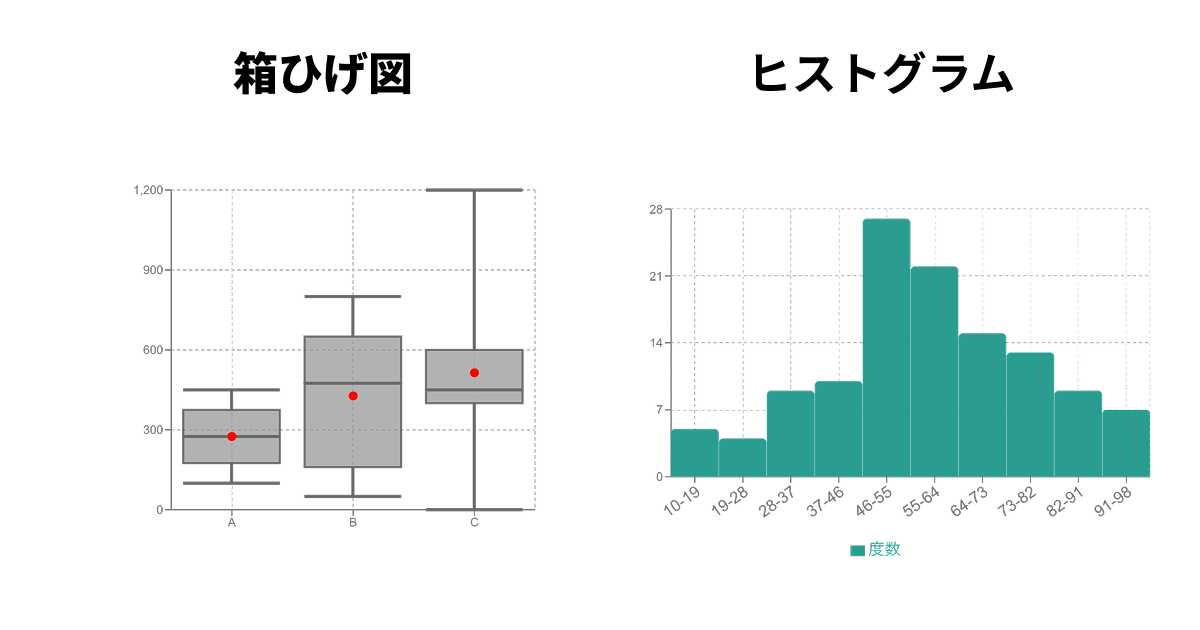
ヒストグラムでも分布は確認できますが、複数のグループを重ねると見づらくなるため、比較には箱ひげ図が適しています。
メリット3:外れ値(異常値)の発見
前述の通り、箱ひげ図は外れ値を視覚的に示してくれます。データ入力のミスや、特異な事象(例:サーバーの異常なアクセス数)を発見する手がかりになります。
箱ひげ図の作り方【簡単ステップ】
箱ひげ図は、統計ソフトやExcel、そして後述するオンラインツールで簡単に作成できます。ここでは、基本的な考え方とツールを使った作成方法を紹介します。
>> Excelでの箱ひげ図の作り方はこちらで解説しています
ステップ1:データを準備する
まずは、グラフにしたいデータを用意します。例えば、あるクラスの数学のテスト結果(30人分)などです。
ステップ2:5数要約(と外れ値)を計算する
次に、データから「最小値」「第1四分位数」「中央値」「第3四分位数」「最大値」を計算します。
(※厳密には、まず四分位数を計算し、外れ値を特定してから最小値・最大値(ひげの端)を決定する手順が一般的です。)
ステップ3:グラフに描画する
計算した数値をもとに、箱とひげを描画します。
ツールを利用する
手計算やExcelでも作成できますが、より手軽に、見た目も美しいグラフを作成したい場合は、専門のオンラインツールが便利です。
「xGrapher(エックスグラファー)」も、Webブラウザ上で簡単に箱ひげ図を作成できるツールです。
xGrapherでは、データをコピー&ペースト(またはCSVファイルをアップロード)するだけで、自動的に箱ひげ図が生成されます。グループごとの比較や、色のカスタマイズも直感的に行えます。
データ分析の第一歩として、ぜひご活用ください。
箱ひげ図の具体的な計算例
実際のデータセットを使用して2つのパターンで計算してみましょう。
例1:データが奇数個 (n=9) の場合
データ: [10, 50, 20, 40, 30, 70, 60, 80, 5]
1. 並べ替え
[5, 10, 20, 30, 40, 50, 60, 70, 80]
2. 中央値 (Q2)
データは9個(奇数)。真ん中の (9+1)/2 = 5番目。
→Q2 = 40
3. Q1, Q3
Q2の「40」を除き、下位・上位に分けます。
下位グループ:
[5, 10, 20, 30](4個)上位グループ:
[50, 60, 70, 80](4個)
下位グループの中央値 (10と20の平均) : Q1 = (10 + 20) / 2 = 15
上位グループの中央値 (60と70の平均) : Q3 = (60 + 70) / 2 = 65
4. 外れ値とひげ
IQR = Q3 - Q1 = 65 - 15 = 50
上限 = 65 + (50 * 1.5) = 140
下限 = 15 - (50 * 1.5) = -60
データは全て-60~140の範囲内なので、外れ値はありません。
最小値 = 5
最大値 = 80
【例1の結果】
最小値(5), Q1(15), Q2(40), Q3(65), 最大値(80)
.png)
例2:データが偶数個 (n=10) の場合(外れ値あり)
データ: [10, 80, 30, 25, 50, 40, 35, 60, 55, 150]
1. 並べ替え
[10, 25, 30, 35, 40, 50, 55, 60, 80, 150]
2. 中央値 (Q2)
データは10個(偶数)。真ん中の5番目(40)と6番目(50)の平均。
→ Q2 = (40 + 50) / 2 = 45
3. Q1, Q3
中央値は計算に使った2つの値の間にあると考え、データを半分に分けます。
下位グループ:
[10, 25, 30, 35, 40](5個)上位グループ:
[50, 55, 60, 80, 150](5個)
→下位グループの中央値 (3番目) : Q1 = 30
→上位グループの中央値 (3番目) : Q3 = 60
4. 外れ値とひげ
IQR = Q3 - Q1 = 60 - 30 = 30
上限 = 60 + (30 * 1.5) = 105
下限 = 30 - (30 * 1.5) = -15
150は上限(105)を超えているため、外れ値です。外れ値 = 150
最小値(ひげの下端): 外れ値を除いた中で最小の
10最大値(ひげの上端): 外れ
150を除いた中で最大の80
【例2の結果】
最小値(10), Q1(30), Q2(45), Q3(60), 最大値(80), 外れ値(150)
.png)
箱ひげ図を使うときの注意点
箱ひげ図は万能ではありません。使う上で知っておきたい注意点が2つあります。
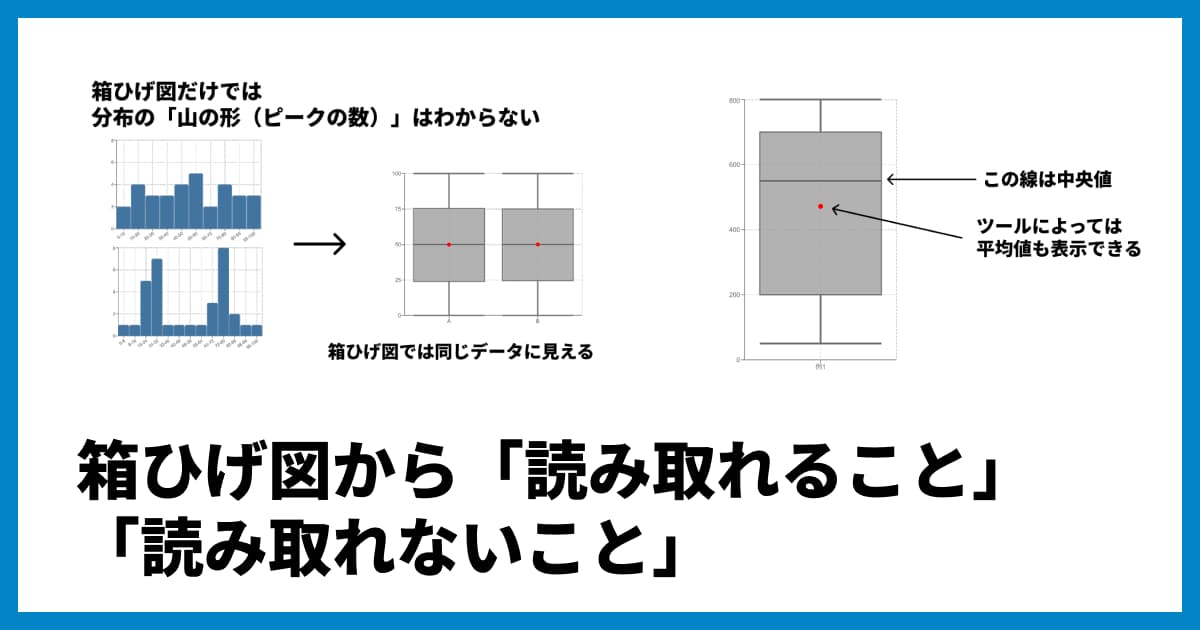
データの「山」がいくつあるかわからない
箱ひげ図はデータを要約して表示するため、分布の「詳細な形状」は失われます。例えば、データが2つのグループ(山が2つある状態、二峰性と言います)に分かれている場合でも、箱ひげ図ではそれが1つの箱として表現されてしまい、特徴を見逃す可能性があります。このような場合は、ヒストグラムを併用するのがおすすめです。
[二峰性が見られるヒストグラムの例]
「ひげ」や「外れ値」の定義が異なる場合がある
この記事では一般的な定義(外れ値を除いた最大・最小までを「ひげ」とする)を紹介しましたが、ツールや分野によっては、「ひげの長さを四分位範囲(IQR)の1.5倍まで」と固定したり、「データの上下10%点まで」をひげとしたり、外れ値の定義が異なる場合があります。グラフを見る際は、そのグラフがどのようなルールで描かれているかを確認することが大切です。
まとめ:箱ひげ図でデータ分析の第一歩を
箱ひげ図(ボックスプロット)は、データのばらつきや分布の特徴を、シンプルかつ視覚的に捉えるための強力なグラフです。
「箱」と「ひげ」で構成される。
5数要約(最小値, Q1, 中央値, Q3, 最大値)が基本。
データのばらつき、偏り、外れ値がわかる。
特に複数グループの比較に強い。
平均点だけを見るのではなく、箱ひげ図を使ってデータの「散らばり具合」にも目を向けることで、データからより多くの情報を読み取ることができます。オンライングラフ作成ツールxGrapherなどを活用して、ぜひ一度、ご自身のデータで箱ひげ図を作成してみてください。
箱ひげ図に関するQ&A
Q1: 箱ひげ図とヒストグラムはどう使い分ければよいですか?
A1: どちらもデータの分布を視覚化するグラフですが、得意なことが異なります。
箱ひげ図: 複数のグループの分布(ばらつき、中央値、外れ値)を比較するのに適しています。
>> 箱ひげ図作成ツールヒストグラム: 1つのデータグループの詳細な分布の形状(山がいくつあるか、どこが一番多いかなど)を見るのに適しています。
両方を併用することで、データをより深く理解できます。
>> ヒストグラム作成ツール
詳細は箱ひげ図とヒストグラムの違いの解説記事をご参照ください。
Q2: 「四分位数」とは何ですか?
A2: データを小さい順に並べたとき、そのデータを4等分する位置にある値のことです。下から25%の位置を「第1四分位数(Q1)」、50%の位置(中央)を「第2四分位数(Q2)=中央値」、75%の位置を「第3四分位数(Q3)」と呼びます。
Q3: 箱が短い(または長い)と、どういう意味ですか?
A3: 箱の長さ(Q1からQ3までの距離)は、データ全体の真ん中50%がどの範囲に収まっているかを示します。
箱が短い: データがその範囲に密集している(ばらつきが小さい)ことを意味します。
箱が長い: データがその範囲で広く散らばっている(ばらつきが大きい)ことを意味します。
Q4: 平均値は箱ひげ図でわかりますか?
A4: 基本的な箱ひげ図には「平均値」は含まれません。箱の中の線は「中央値」です。平均値は外れ値の影響を受けやすいですが、中央値は受けにくいため、データの中心を見る指標として使われます。ただし、ツールによってはオプションで平均値を「×」印などで同時に表示できるものもあります。
Q5: 箱ひげ図はどんなデータに使えますか?
A5: テストの点数、身長、体重、気温、売上、製品の重さ、サイトの滞在時間など、数値で表されるデータ(量的データ)の分析に使われます。特に、複数のグループ(例:クラス別、地域別、男女別など)に分けて、それらの分布を比較したい場合に非常に有効です。
参考記事: 箱ひげ図の身近な例3選!テストの点数や気温など
Q6: 箱ひげ図とバイオリンプロットはどう使い分ければよいですか?
A6: シンプルに中央値やデータの広がり(四分位範囲)を要約・比較したい場合は「箱ひげ図」が適しています。一方、データが二極化していないか(山の数)や、分布の詳しい「形」そのものを詳細に比較したい場合は「バイオリンプロット」を使うと、より多くの情報を得られます。
>> バイオリンプロットに関する解説記事
>> バイオリンプロット作成無料ツール
)
)
)
)
)
)
)
)
)
)
)