【図解】箱ひげ図の四分位数の求め方を徹底解説！データの偶数・奇数やエクセルとの違いとは？

四分位数（しぶんいすう）とは？基本のおさらい

具体的な計算に入る前に、まずは四分位数が何を表しているのかを整理しておきましょう。

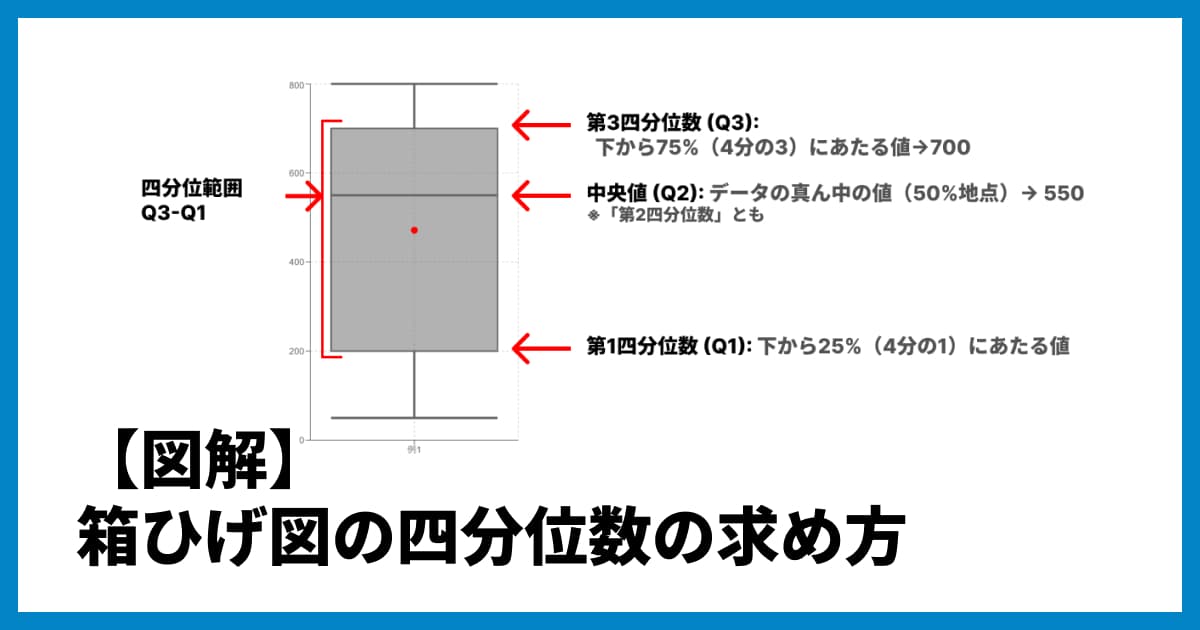
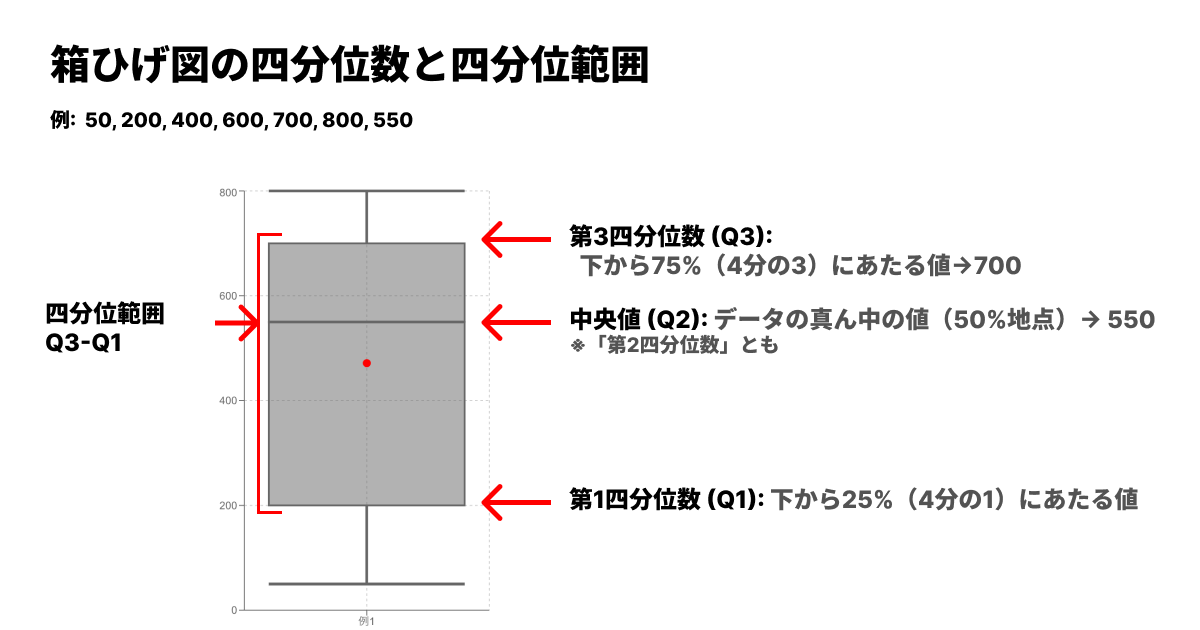
四分位数とは、データを小さい順（昇順）に並べたとき、データの個数で等しく4分割する位置にある値のことです。箱ひげ図においては、「箱」の部分と「中央の線」を形成する重要な要素です。

• 第一四分位数 ($Q1$): データの下位25%の地点にある値（箱の下底）

• 第二四分位数 ($Q2$): データの中央値（箱の中にある線）

• 第三四分位数 ($Q3$): データの上位25%（下から75%）の地点にある値（箱の上底）

これらを求めることで、データがどのあたりに集中しているのかが一目でわかるようになります。

箱ひげ図自体の基本的な見方や用語については、以下の記事で詳しく解説していますので、あわせてご覧ください。

参考記事: 箱ひげ図の基本や作り方

【実践】具体例を用いた四分位数の求め方（手計算の基本）

ここでは、日本の学校教育（数学Iなど）で一般的に扱われる求め方（ヒンジとも呼ばれます）を解説します。ポイントは「データの個数が奇数か偶数か」で手順が少し変わる点です。

1. データの個数が「奇数」の場合

データが奇数個の場合、真ん中の数字が一つに決まるためシンプルです。

手順:

1. データを小さい順に並べる。

2. 真ん中の値を第二四分位数 ($Q2$ / 中央値) とする。

3. 中央値を除いた、下位グループ（前半）の中央値を第一四分位数 ($Q1$) とする。

4. 中央値を除いた、上位グループ（後半）の中央値を第三四分位数 ($Q3$) とする。

具体例：データが7個の場合 {1, 3, 5, 7, 9, 11, 13}

• 中央値 ($Q2$) は 7

• 下位グループ {1, 3, 5} の中央値 ($Q1$) は 3

• 上位グループ {9, 11, 13} の中央値 ($Q3$) は 11

2. データの個数が「偶数」の場合

データが偶数個の場合、真ん中に数字が存在しないため、平均をとって計算します。

手順:

1. データを小さい順に並べる。

2. 中央にある2つの値の平均を第二四分位数 ($Q2$ / 中央値) とする。

3. データを中央で前半と後半に分ける（中央値の計算に使った値も含めて分ける）。

4. 前半グループの中央値を第一四分位数 ($Q1$) とする。

5. 後半グループの中央値を第三四分位数 ($Q3$) とする。

例：データが8個の場合 {2, 4, 6, 8, 10, 12, 14, 16}

• 中央の2つは8と10。よって $Q2 = (8+10) \div 2 =$ 9

• 前半グループ {2, 4, 6, 8} の中央値は (4+6) ÷ 2 なので $Q1 =$ 5

• 後半グループ {10, 12, 14, 16} の中央値は (12+14) ÷ 2 なので $Q3 =$ 13

このように、手計算で行う場合は「中央値を見つけて、データを半分に割り、さらにその中央値を見つける」というステップを繰り返します。

注意！Excelと手計算で結果がズレる理由

「学校で習った通りに計算したのに、Excelで計算したら値が違う…」
このような経験はありませんか？

実は、四分位数の定義には世界的に統一されたものがなく、「データをどう分割するか」という考え方が異なるため、計算結果にズレが生じます。

具体的に、シンプルなデータ {1, 2, 3, 4, 5} （5つの数字）で比較してみましょう。

1. 学校数学（ヒンジ）の考え方

学校で習う方法は、物理的にデータを半分に分けるイメージです。

1. 中央値は 3 です。

2. 3を除いた前半グループは {1, 2} です。

3. この前半グループの真ん中（平均）を $Q1$ とします。

   • $(1 + 2) \div 2 = \mathbf{1.5}$

つまり、手計算（ヒンジ）での $Q1$ は 1.5 になります。

2. Excel（QUARTILE.INC関数）の考え方

Excel（特にINC関数）は、「順位（パーセンテージ）」で位置を特定するイメージです。

Excelは「5個あるデータのうち、0%地点が先頭(1)、100%地点が最後尾(5)」という数直線のような目盛りを作ります。その上で「25%地点にある値」を計算で割り出します。

この計算式（ $(n-1) \times 0.25 + 1$ 番目）に当てはめると、5個のデータの25%地点は、ちょうど 2番目のデータ という結果になります。

• 2番目のデータは 2 なので、Excelでの $Q1$ は 2 になります。

どちらが正解なのか？

結論から言うと、どちらも間違いではありません。

• 学校数学（ヒンジ）: データの分布をざっくりとブロック分けして見るのに適しています。

• Excel（統計学）: データ量が多い場合や、より厳密な統計解析（標準偏差などとの兼ね合い）を行う際に適しています。

このように定義が異なるため、「学校の宿題の検算にExcelを使う」と、答えが合わずに混乱することになります。
学校の課題であれば手計算のルールに従い、ビジネスや研究でのデータ分析ならExcelや統計ソフトの数値を使う、という使い分けが重要です。

Excelでの詳しい作成方法や関数の違いについては、こちらの記事で深掘りしています。

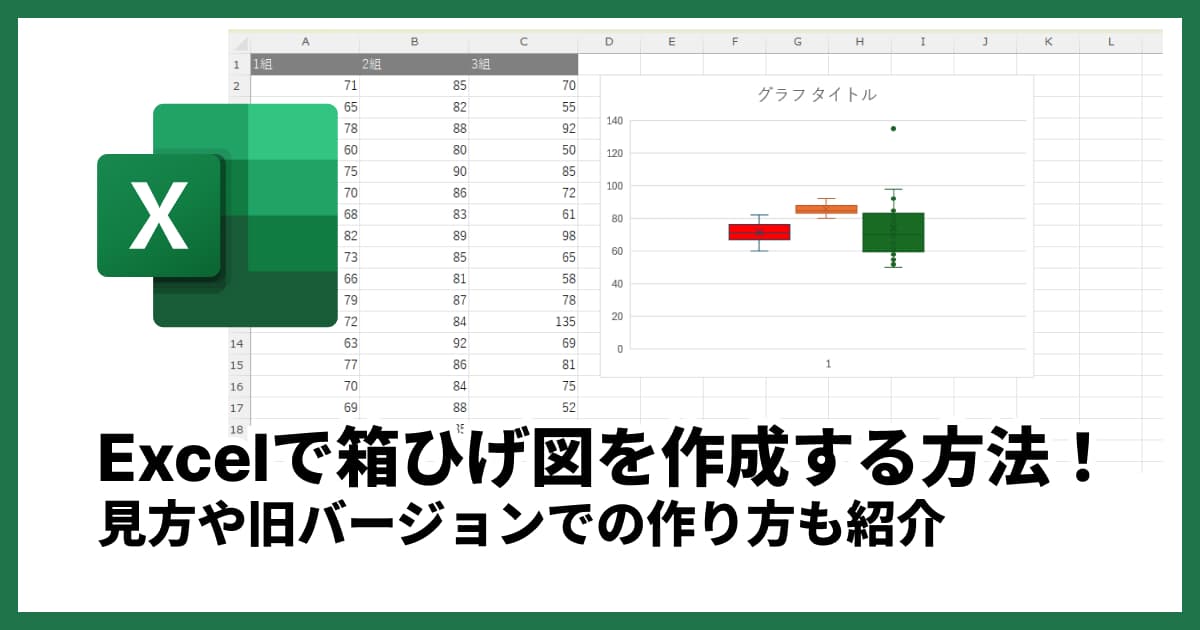
Excelで箱ひげ図を作成する方法を徹底解説！簡単な作り方も紹介

計算不要！正確な箱ひげ図を瞬時に作る方法

四分位数の計算は、データの数が数十、数百となると手作業では限界があります。また、先ほど説明したような定義の違いによるミスも起きがちです。

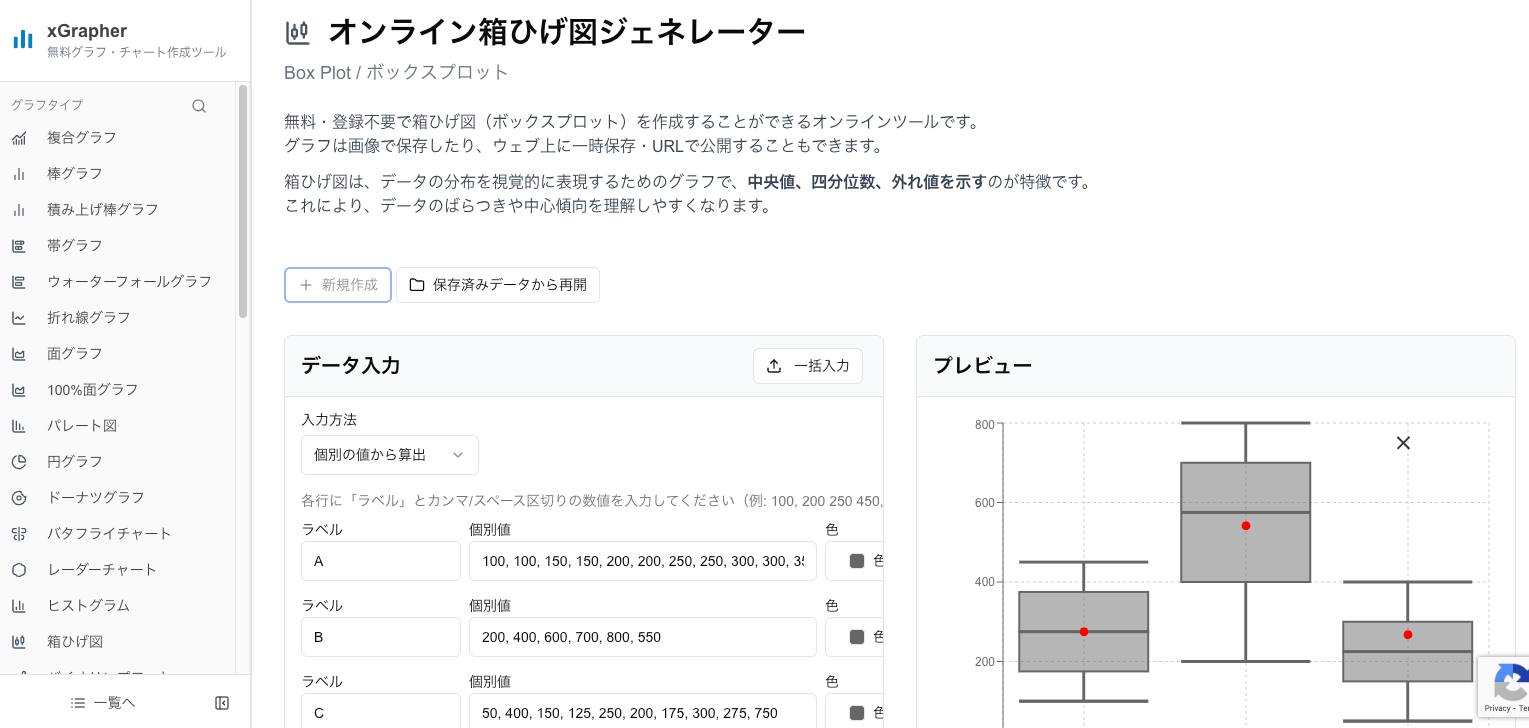
そこでおすすめなのが、Web上で簡単にグラフ作成ができるツール xGrapher です。

xGrapher の箱ひげ図作成ツールを使えば、以下のメリットがあります：

• 計算不要: データを貼り付けるだけで、Q1, Q2, Q3を自動計算します。

• 外れ値の自動判定: 四分位範囲（IQR）に基づいた外れ値の除外・表示も自動で行えます。

• 美しいデザイン: プレゼンやレポートにそのまま使えるデザインのグラフが即座に完成します。

Excel操作に不慣れな方や、計算ミスを防ぎたい方は、ぜひ一度試してみてください。登録なしで無料で使い始めることができます。

👉 xGrapherで箱ひげ図を作ってみる

ちなみに、四分位範囲を使った外れ値の詳しい判定基準については、以下の記事が参考になります。

箱ひげ図の外れ値とは？基準（1.5倍）の求め方と見つけた時の対処法を解説

四分位数から分かること・分からないこと

四分位数を正しく求められれば、データ分布の歪み具合が見えてきます。

• 例A: 中央値 ($Q2$) が箱の中心より下にある: データが小さい値に寄っている、あるいは大きな値の方に裾が長い分布。

• 例B: 箱の長さ ($Q3 - Q1$) が長い: データの中央付近がばらついている。

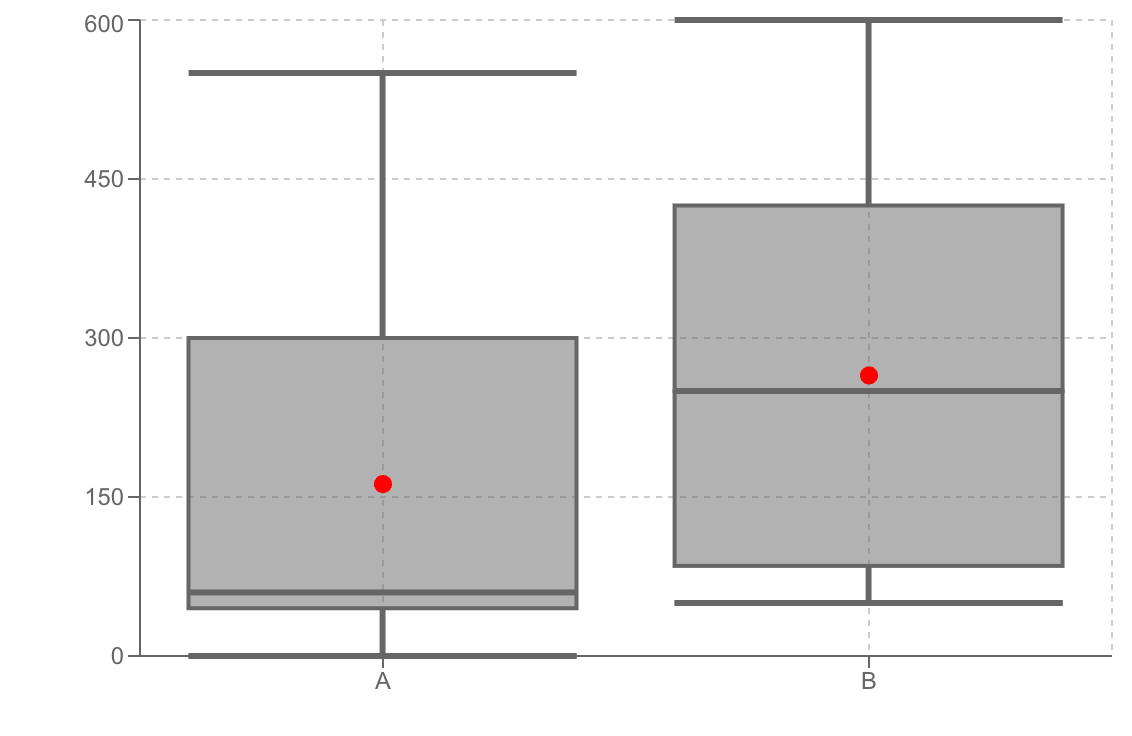
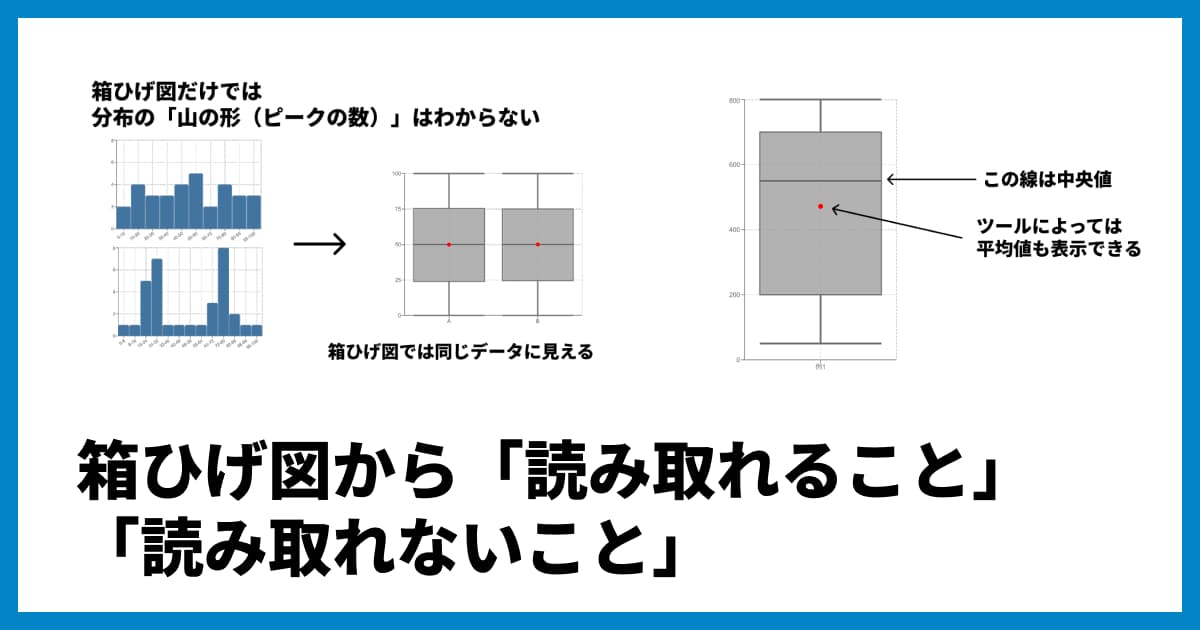
ただし、箱ひげ図だけでは「データの山がいくつあるか（二峰性など）」までは読み取れません。データの詳細な分布形状を知りたい場合は、ヒストグラムやバイオリン図と併用するのがベストです。

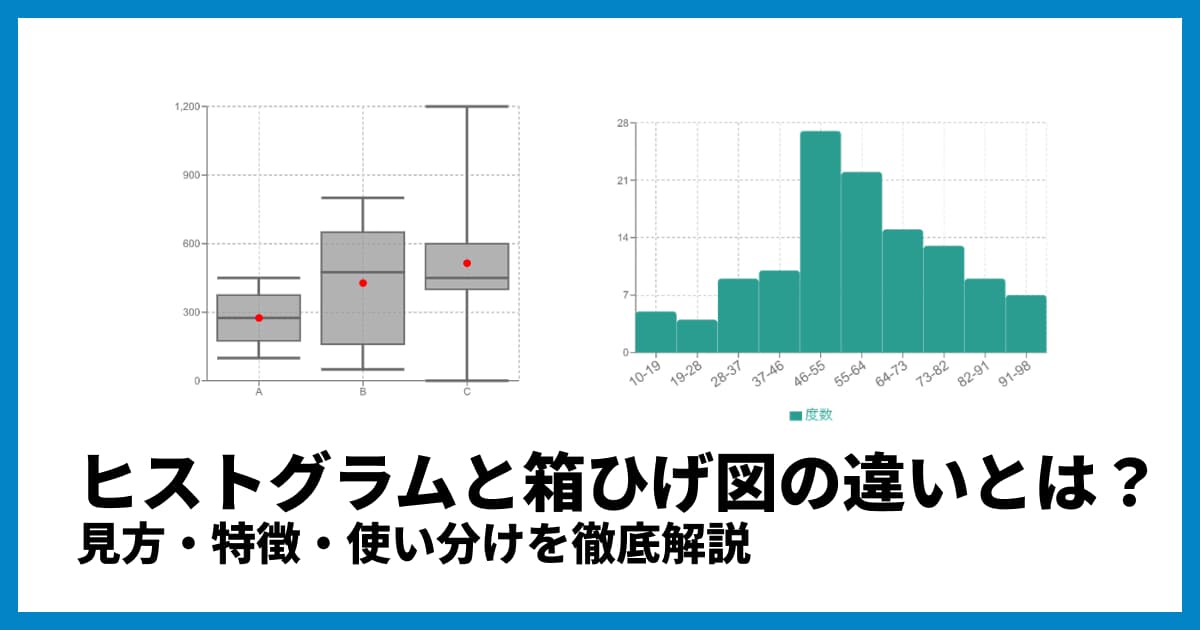
各グラフの使い分けについては、以下の記事も参考にしてください。

• ヒストグラムと箱ひげ図の違いとは？見方・特徴・使い分けを徹底解説

• バイオリンプロットとは？ 見方、ヒストグラムや箱ひげ図との違いを徹底解説！

• 箱ひげ図の見方「読み取れること・読み取れないこと」を完全解説！

まとめ

箱ひげ図を作成するための「四分位数」の求め方について解説しました。

• 基本の手順: データを順に並べ、中央値 ($Q2$) を決めてから、前半・後半それぞれの中央値 ($Q1, Q3$) を求める。

• 偶数と奇数の違い: データの個数によって中央値の取り方が変わるため注意が必要。

• 計算のズレ: 学校で習う方法とExcelなどの統計ソフトでは計算ロジック（定義）が異なる場合がある。

正確なデータ分析を行うためには、手計算のロジックを理解しつつ、実務ではxGrapherのような専用ツールを使って効率化するのが一番の近道です。ぜひ目的に合わせて最適な方法を選んでください。

よくある質問 (Q&A)

Q1. 四分位数と四分位範囲（IQR）の違いは何ですか？

A1. 四分位数は「位置」を表す値（$Q1, Q3$など）です。一方、四分位範囲（IQR: Interquartile Range）は「幅」を表す値で、$Q3 - Q1$ で計算されます。箱ひげ図の「箱の長さ」が四分位範囲に該当し、データの中央50%がどのくらいの範囲に散らばっているかを示します。

Q2. データの個数が4個の場合の四分位数はどうなりますか？

A2. 手計算（ヒンジ）の場合、データ {10, 20, 30, 40} で考えると：
中央値 ($Q2$) は (20+30)÷2 = 25。
前半 {10, 20} の中央値 ($Q1$) は 15。
後半 {30, 40} の中央値 ($Q3$) は 35 となります。
このようにデータ数が少なくても手順は同じです。

Q3. エクセルの QUARTILE.INC と QUARTILE.EXC はどちらを使えばいいですか？

A3. 一般的な統計解析では QUARTILE.INC（0%と100%を含む定義）が使われることが多いですが、データの範囲外への推測を含めたい場合などは QUARTILE.EXC が使われます。日本の学校数学の定義に近いのは、実はExcelの関数には標準搭載されていません。学校数学と同じ値を出したい場合は手計算のロジックに従うか、xGrapherのようなツールの利用をおすすめします。

Q4. 外れ値はどうやって計算するのですか？

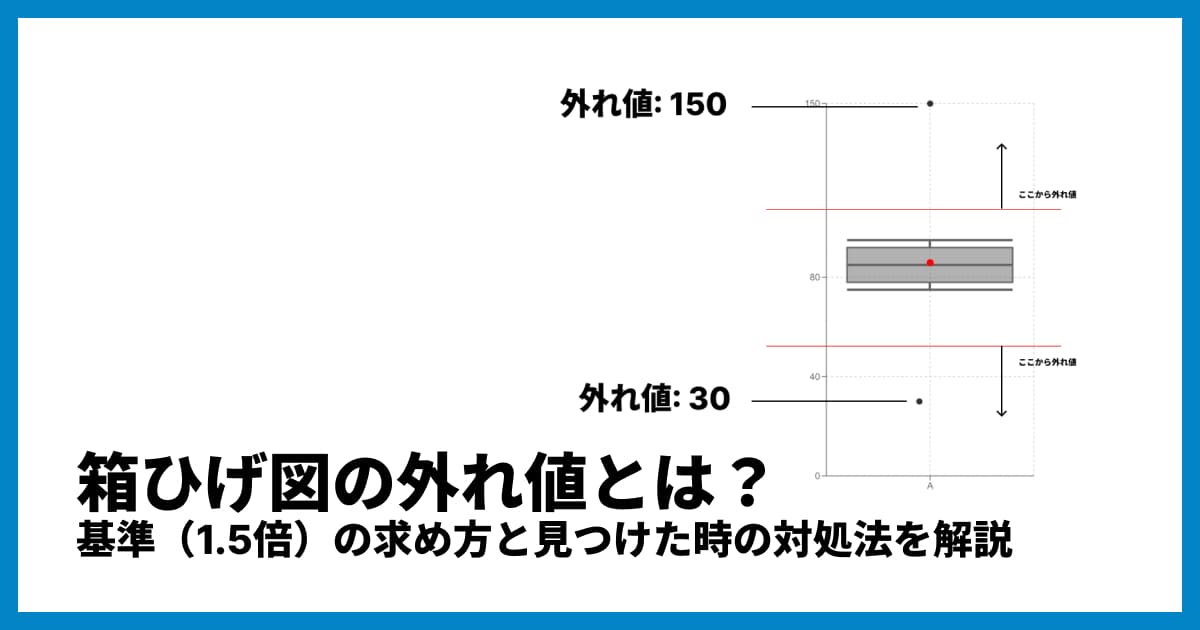
A4. 一般的には、以下の基準を超えた値を外れ値とします。

• 下側の外れ値：$Q1 - 1.5 \times \text{IQR}$ 未満

• 上側の外れ値：$Q3 + 1.5 \times \text{IQR}$ 超
  四分位範囲（IQR）の1.5倍以上離れた値は、異常値として「ひげ」の外に点でプロットされることが一般的です。

Q5. 四分位数はどんな時に役立ちますか？

A5. 平均値だけでは見えない「データの偏り」を知りたい時に役立ちます。例えば「平均年収」だけだと一部の大富豪に数値が引き上げられますが、四分位数や中央値を見れば「一般的な大多数の人がどのくらいの年収か」をより正確に把握できます。
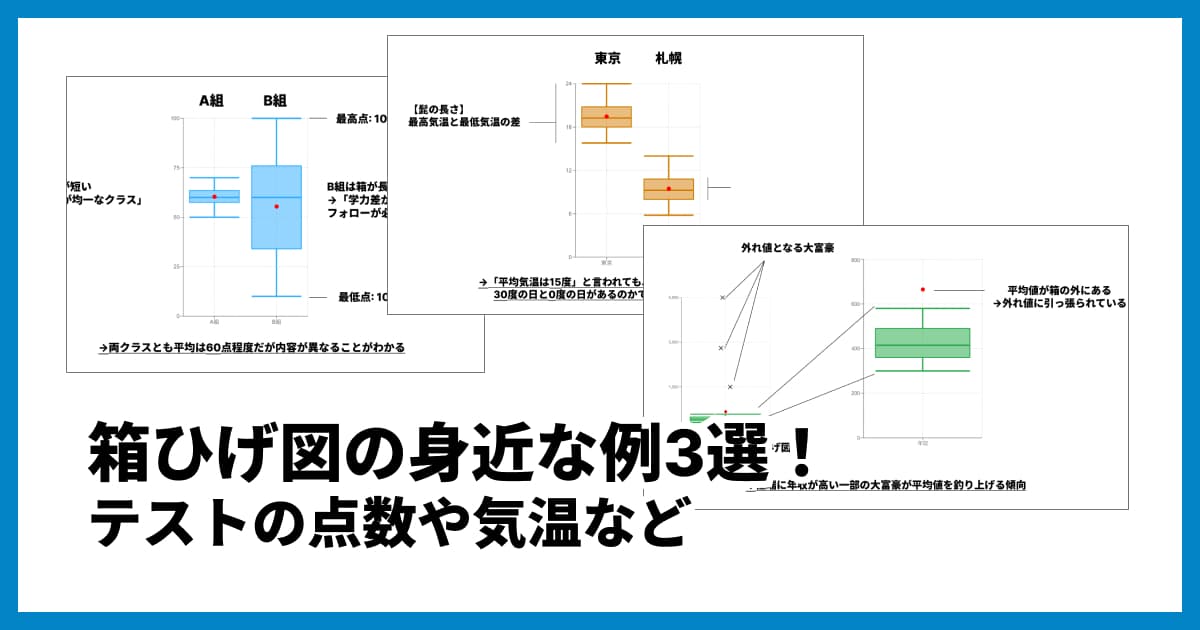
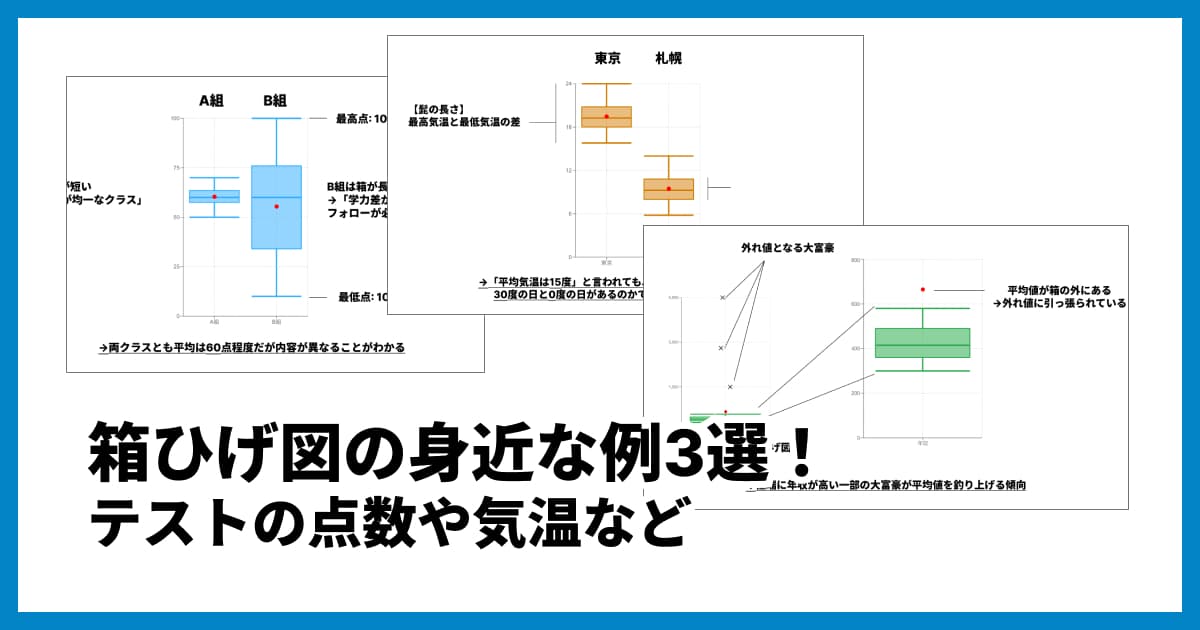
参考記事: 箱ひげ図の身近な例3選！テストの点数や気温など、平均値だけでは見えないデータの真実とは？