【図解】ボロノイ図とは？仕組み、面白い活用事例、簡単な作り方を世界一わかりやすく解説

ボロノイ図とは？～一番近い点で縄張りを作る～

ボロノイ図を一言で説明すると、「平面上に置かれた複数の点に対して、どの点に一番近いかによって領域分けした図」のことです。領域内のどの場所をとっても、他のどの点よりも、その領域の母点と呼ばれる中心点が一番近い、という性質があります。

[ボロノイ図の例]

なんだか少し難しいでしょうか？では、もっと身近な例で考えてみましょう。

身近な例：コンビニの勢力図

例えば、あなたの街の地図に、いくつかのコンビニ（A店、B店、C店…）の場所を点でプロットします。そして、「どのコンビニが一番近いか」で地図を色分けしていくと、自然と各コンビニの「縄張り」のようなものが見えてきます。この縄張りこそが、ボロノイ図です。

A店の領域内であれば、他のどのコンビニよりもA店が一番近く、B店の領域に一歩足を踏み入れると、今度はB店が最寄りになります。この領域の境界線は、ちょうど両方のコンビニから等しい距離になる点の集まりです。

「垂直二等分線」が鍵！仕組みを簡単解説

ボロノイ図の境界線は、どうやって引かれているのでしょうか。その鍵を握るのが、中学校の数学で習った「垂直二等分線」です。

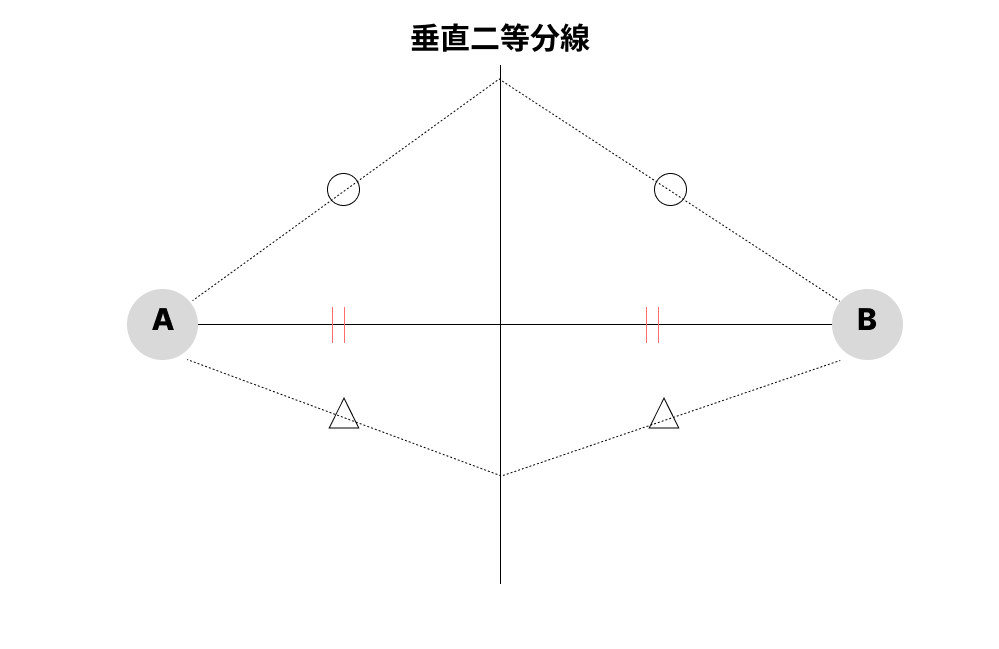
2つの母点（例えばA店とB店）があったとき、この2点を結んだ線分の垂直二等分線を引くと、その線上にある点はA店からもB店からも距離が等しくなります。

ボロノイ図は、隣り合うすべての母点のペアに対してこの垂直二等分線を引いていき、それらを繋ぎ合わせることで作成されているのです。とてもシンプルで合理的な仕組みだということがわかりますね。

ボロノイ図って何の役に立つの？面白い活用事例7選

そのシンプルな成り立ちとは裏腹に、ボロノイ図は非常にパワフルで、様々な分野で活用されています。ここでは、その面白い活用事例を7つご紹介します。

1. 【都市計画】公共施設の最適な配置
   学校や消防署、郵便局などを新しく設置する際に、ボロノイ図を使って住民が最もアクセスしやすい場所を割り出すことができます。住民がいない広いエリアを見つけ、そこをカバーする形で配置計画を立てるのに役立ちます。

2. 【マーケティング】店舗の商圏分析
   先ほどのコンビニの例のように、自社や競合の店舗を地図上にプロットすることで、各店舗が影響を及ぼす範囲（商圏）を可視化できます。まだカバーできていない空白地帯を見つけ出し、新規出店の戦略を立てるのに有効です。

3. 【生態学】動植物の縄張り分析
   動物の巣や、特定の植物が生えている場所を母点としてボロノイ図を作成すると、その生物の縄張りやテリトリーの大きさを推定することができます。

4. 【通信】携帯電話の基地局の電波範囲
   各基地局を母点とすることで、どの基地局の電波を最も強く受信できるエリアなのかをモデル化できます。これにより、電波の届きにくいエリアを特定し、新しい基地局の設置計画に役立てます。

5. 【気象学】降雨量の推定
   観測所が点在している場合、ある地点の降雨量は、最も近い観測所のデータに影響されると考えられます。ボロノイ図で各観測所の担当エリアを決め、エリア全体の降雨量を推定する手法（ティーセン法）があります。

6. 【アート・デザイン】美しいボロノイパターン
   ボロノイ図が作り出す独特の細胞のようなパターンは、デザインの世界でも人気です。キリンの模様やトンボの翅脈（しみゃく）も、自然界が生んだボロノイ図の一種と見ることができ、建築物の壁面デザインやアクセサリー、CGアートなどに応用されています。

7. 【ゲーム開発】マップの自動生成
   ゲームの世界で、自然な地形や国の境界線を自動生成する際にボロノイ図のアルゴリズムが使われることがあります。ランダムな点を配置するだけで、リアルな分割マップを手軽に作成できます。

オンラインツールで簡単作成！xGrapherを使ってみよう

これほどまでに便利なボロノイ図ですが、「作るのが難しそう…」と感じるかもしれません。プログラミングや専門のGISソフトが必要な場合も多いですが、ご安心ください。

当サイトが運営するオンライングラフ作成ツール「xGrapher」なら、Webブラウザ上で、誰でも無料で直感的にボロノイ図を作成できます。

プログラミング不要でボロノイ図を作成

xGrapherの魅力は、その手軽さです。

• インストール不要：Webサイトにアクセスするだけですぐに利用可能。

• 直感的な操作：母点となるデータの数値を入力、またはCSVファイルをアップロードするだけ。

• カスタマイズも自由：色や線の太さなどを自由に調整し、美しいボロノイ図をデザインできます。

作成したボロノイ図は、画像としてダウンロードできるので、レポートやプレゼンテーション資料にもすぐに活用いただけます。

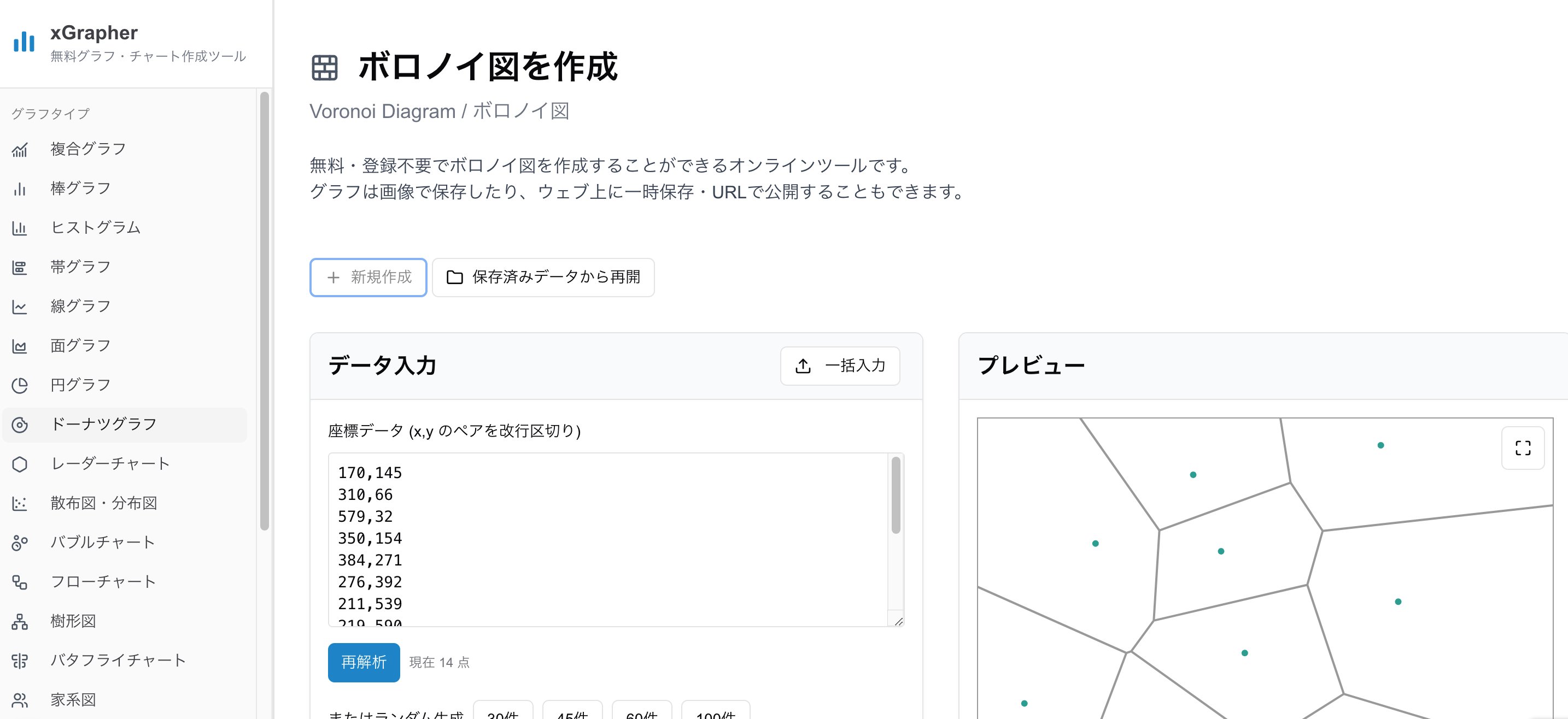
利用手順は以下の通りです。

1. xGrapherのボロノイ図作成ページへアクセス

2. 下地となる地図などの画像がある場合は「下地画像を選択」からファイルを選択

3. 座標データを入力するか、母点となるポイントをマウスでクリックすれば簡単にボロノイ図を作成できます。

4. 完成したボロノイ図は画像としてダウンロード可能です。

他のグラフとの組み合わせでデータ分析を深めよう

xGrapherはボロノイ図専門のツールではありません。散布図やバブルチャートなど、多彩なグラフを作成できる総合的なデータ可視化ツールです。

例えば、まず散布図でデータの分布を確認し、そのデータ点を母点としてボロノイ図を重ねて表示することで、「データの密集度」と「各点がカバーする領域の広さ」を同時に分析できます。これにより、データに隠された新たなインサイトを発見できるかもしれません。

データ分析の第一歩として、まずはxGrapherでデータの可視化を始めてみませんか？

もっと知りたい人へ：ドロネー図との関係

ボロノイ図について調べていると、必ずと言っていいほど「ドロネー図」という言葉が出てきます。この2つは、切っても切れない深い関係にあります。

ドロネー図とは、ボロノイ図で隣り合っている領域の母点同士を線で結んでできる三角形のネットワークのことです。

• ボロノイ図: 点からの「距離」に着目して面を作る。

• ドロネー図: 点同士の「隣接関係」に着目して線を作る。

この2つは、片方がわかればもう片方もわかる「双対（そうつい）グラフ」という関係にあり、データ分析やシミュレーションの世界でセットでよく用いられます。

ドロネー図はただ闇雲に点を繋げるだけではありません。詳しい解説はこちらの記事をご参照ください。

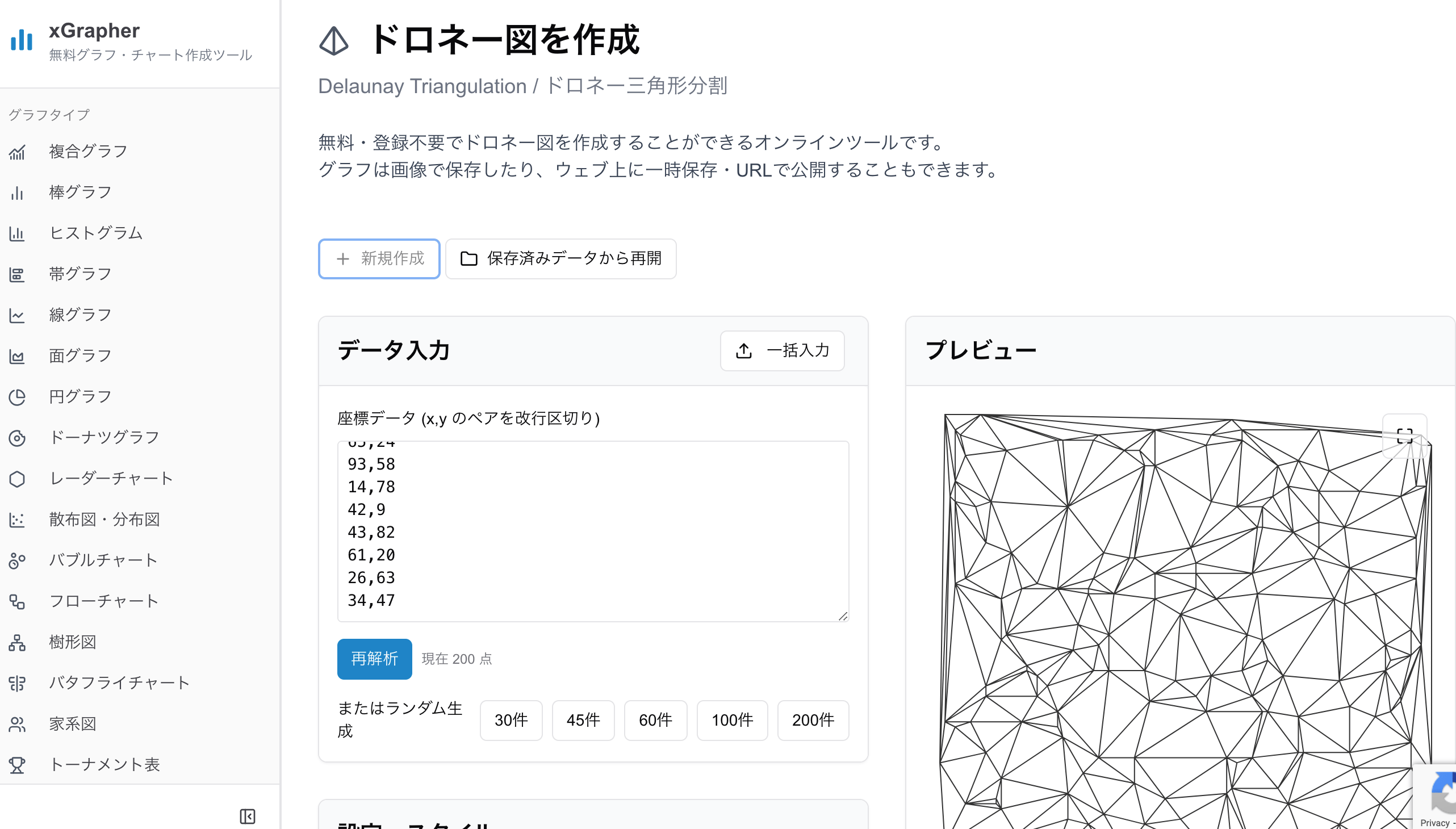
ドロネー図を作成するには？

前述のxGrapherではドロネー図も作成することができます。座標のデータの入力方法はボロネイ図と同じでクリックするか入力することもできます。

> xGrapherのドロネー図作成ページ

ボロノイ図に関するQ&A

Q1. ボロノイ図の名前の由来は？

A1. 20世紀初頭に活躍したウクライナの数学者、ゲオルギ・フェオドシエビッチ・ボロノイ氏の名前に由来します。彼の功績を称えて「ボロノイ図」と呼ばれるようになりました。

Q2. ボロノイ図とドロネー図の簡単な違いは？

A2. 最も簡単な見分け方は、ボロノイ図が「領域（面）」の集まりであるのに対し、ドロネー図は「三角形（線）」の集まりである点です。母点間の縄張り図がボロノイ図、母点間の最短の道筋ネットワークがドロネー図とイメージすると良いでしょう。

Q3. どんなデータがあればボロノイ図を作れますか？

A3. 各母点の位置を示す「座標データ」があれば作成できます。具体的には、X座標とY座標のペアのリスト（例: (x1, y1), (x2, y2), ...）があれば十分です。店舗の緯度経度データや、グラフ上の点の座標などが該当します。

Q4. ボロノイ図の計算は難しいですか？

A4. 手書きで正確に描くのは点の数が増えると大変ですが、コンピュータのアルゴリズムを使えば高速に計算できます。「フォーチュンのアルゴリズム」などが有名です。xGrapherのようなツールを使えば、ユーザーは難しい計算を意識することなく、瞬時に結果を得ることができます。

Q5. スマホでもボロノイ図は作れますか？

A5. はい、作成できます。xGrapherはスマートフォンやタブレットのブラウザにも対応しているため、いつでもどこでも手軽にボロノイ図を作成し、データを可視化することが可能です。

まとめ

この記事では、ボロノイ図の基本的な概念から、その仕組み、驚くほど広い分野での活用事例、そしてオンラインツール「xGrapher」を使った簡単な作成方法までをご紹介しました。

• ボロノイ図は「一番近い点」で縄張りを作る、シンプルで強力な図。

• 都市計画からアートまで、様々な分野で活用されている。

• 鍵となる仕組みは「垂直二等分線」。

• xGrapherを使えば、誰でも無料で、簡単にボロノイ図を作成できる。

一見すると専門的に見えるボロノイ図も、その本質を理解すれば、あなたのデータ分析やアイデアを可視化するための強力な武器になります。

ぜひ、xGrapherを使って、あなた自身のデータでボロノイ図の作成を体験してみてください。きっと新しい発見があるはずです。