ドロネー図とは？ボロノイ図との関係や活用事例を世界一わかりやすく解説

ドロネー図とは？ - 「空の円」が作る最適な三角形分割

ドロネー図をひとことで言うと、「与えられた点の集まりを、できるだけ『ずんぐりむっくり』な三角形で埋め尽くす方法」です。

なぜ、わざわざ「ずんぐりむっくり」（三角形の最小角が大きい）な三角形が良いのでしょうか。それは、細長くて鋭角な三角形をできるだけ避けることで、後述するシミュレーションやCGモデリングで安定した結果を得やすくなるからです。

この「最適な」三角形分割を実現するために、ドロネー図はたった一つの、しかし非常に強力なルールに従います。それが「空の円（からのえん）の性質」です。

空の円の性質とは？

空の円の性質とは作成されたどの三角形の外接円（3つの頂点を通る円）を考えても、その円の内部に他の点は一つも含まれない性質のことです。（ただし境界上に乗る場合は許される）

このルールを守ることで、必然的に細長い三角形が最小化され、全体としてバランスの取れた三角形のネットワークが生まれるのです。この性質が、ドロネー図を単なる三角形分割以上の特別な存在にしています。

ボロノイ図との深い関係 - 双対（そうつい）という裏表の存在

ドロネー図を語る上で絶対に欠かせないのが、ボロノイ図の存在です。実はこの二つ、コインの裏表のような切っても切れない関係にあり、専門的には「双対（そうつい）グラフ」と呼ばれています。

• ボロノイ図: 「各点に一番近い領域」を表す図。各点の「勢力範囲」を示します。

• ドロネー図: 「どの点が隣接しているか」を表す図。点と点の「関係性」を示します。

実は、一方の図からもう一方の図を簡単に作ることができます。

• ボロノイ図の各領域の母点（中心の点）同士を線で結ぶと、ドロネー図が現れます。

• ドロネー図の各三角形の外接円の中心を結ぶと、ボロノイ図の頂点が現れます。

このように、二つは互いを定義し合う関係性を持っているのです。

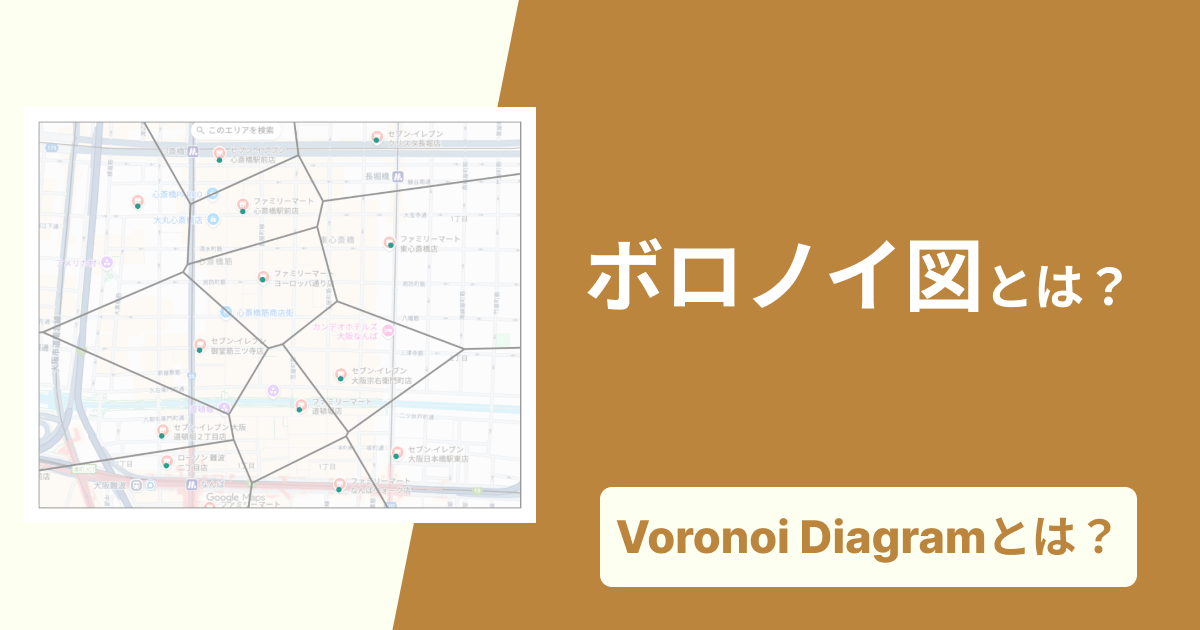
ボロノイ図についてより詳しく知りたい方は、ぜひこちらのボロノイ図に関する記事もご覧ください。二つの図を見比べることで、データが持つ二つの側面（領域と関係性）を深く理解できます。

ドロネー図の身近な活用事例 - CGから地形データまで

ドロネー図の「美しく安定した三角形を作る」性質は、様々な分野で応用されています。

1. コンピュータグラフィックス (CG) と3Dモデリング

3Dモデルの表面は、ポリゴンと呼ばれる小さな多角形（多くは三角形）の集まりでできています。ドロネー図（正確にはドロネー三角形分割）を利用することで、歪みの少ない滑らかな曲面を効率的に表現できます。ゲームのキャラクターや映画のVFXなど、リアルなCG制作の基礎を支える技術です。

2. 地理情報システム (GIS) と地形モデリング

地図データや測量で得られた標高データ（点の集まり）から、滑らかな地形モデル（TIN: 不整三角網）を生成する際にドロネー図が活躍します。これにより、リアルな3Dマップの作成や、洪水シミュレーション、日照計算などが可能になります。

3. 科学技術シミュレーション

物理シミュレーションや構造解析で使われる「有限要素法」では、解析対象を小さな要素（三角形など）に分割して計算します。ドロネー図によって生成された質の良い三角形は、計算の精度と安定性を高めるために不可欠です。

このように、ドロネー図はバラバラの点群データに構造を与え、意味のある情報へと変換するための強力なツールなのです。

xGrapherでデータ可視化を始めよう

ドロネー図のような複雑なグラフを手作業で作成するのは大変です。そこでおすすめなのがオンライングラフ作成ツールxGrapherです。

• 無料・登録不要

• オンラインで利用可能（アプリやシステムのインストール不要）

• データは貼り付けるだけで完成、グラフのダウンロードも可能

お手元のデータをアップロードするだけで、ドロネー図の他、散布図や折れ線グラフなどを誰でも簡単に作成できます。

利用方法:

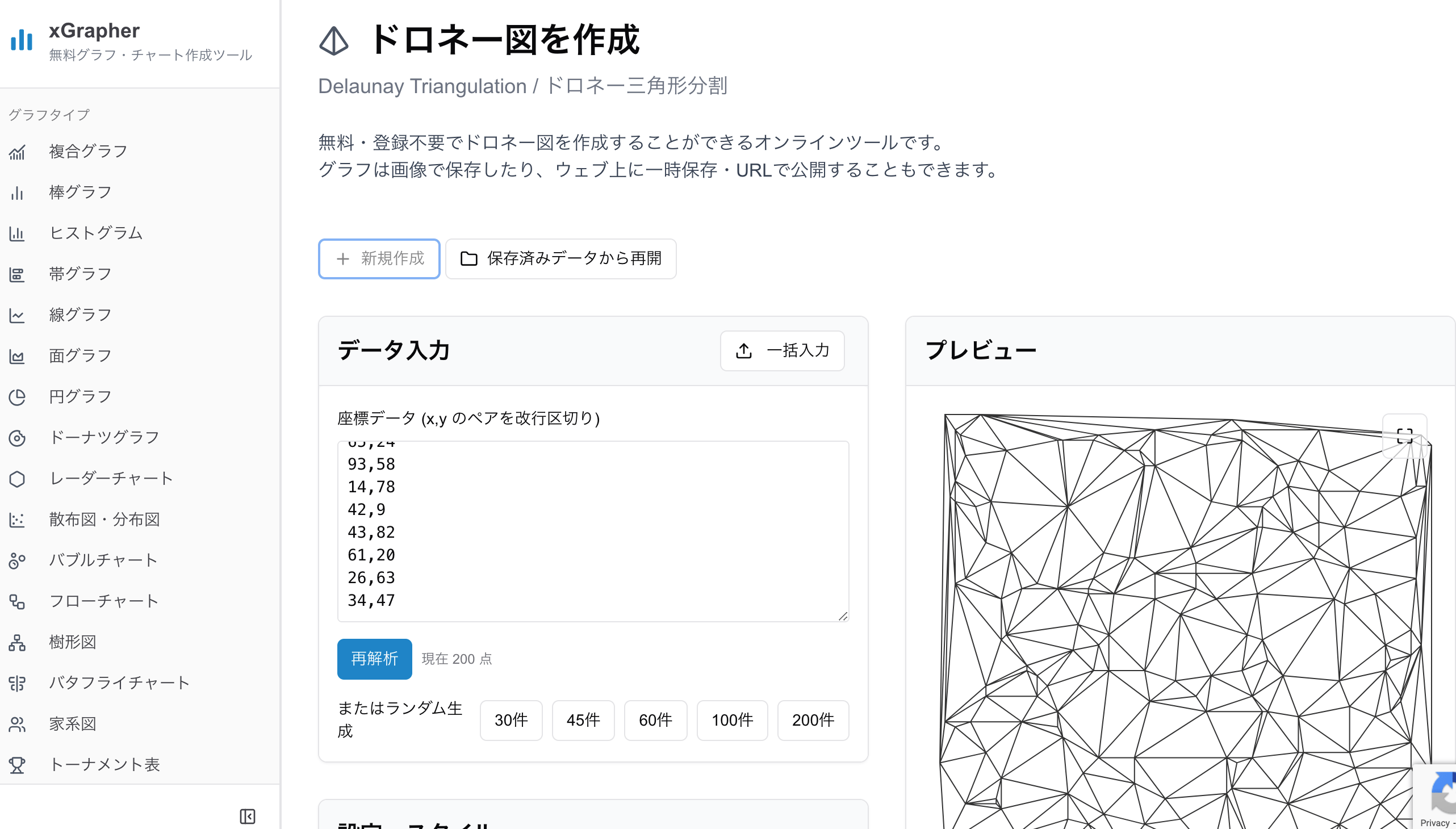
1. xGrapherのドロネー図作成機能へアクセス

2. 下地となる地図などの画像がある場合は「下地画像を選択」からファイルを選択

3. 座標データを入力するか、母点となるポイントをマウスでクリックすれば簡単にドロネー図を作成できます。

4. 完成したドロネー図は画像としてダウンロード可能です。

ぜひ試してみてください。

ドロネー図に関するQ&A

Q1. ドロネー図の最も重要なルールは何ですか？
A1. 「空の円の性質」です。すべての三角形の外接円の内部に、その三角形の頂点以外の点が含まれないというルールが、ドロネー図を特徴づけています。

Q2. ボロノイ図とドロネー図はどう違うのですか？
A2. ボロノイ図が各点の「領域（縄張り）」を示すのに対し、ドロネー図は点同士の「隣接関係」を示します。これらは互いに双対（裏表）の関係にあります。

Q3. なぜ細長い三角形は良くないとされるのですか？
A3. CGのレンダリングや物理シミュレーションにおいて、角度が極端に鋭い三角形は計算誤差が大きくなり、結果が不安定になる原因となるためです。ドロネー図はこれをできるだけ避ける性質があります。

Q4. ドロネー図の名前の由来は何ですか？
A4. 20世紀初頭にこの概念を考案したロシアの数学者、ボリス・ドロネー (Boris Delaunay) の名前に由来しています。

Q5. ドロネー図は自分で手書きできますか？
A5. 点の数が少なければ、外接円を描きながらルールに従って手で描くことも可能です。しかし、点の数が多くなると組み合わせが爆発的に増えるため、通常はコンピュータを用いて計算するのがおすすめです。

まとめ：点の集まりに「意味」を与えるドロネー図

本記事では、点群を最も安定的で美しい三角形で繋ぐ「ドロネー図」について解説しました。

最後に、重要なポイントを振り返りましょう。

• 最適な三角形分割: ドロネー図は「空の円の性質」というルールに基づき、細長い三角形を避けて点を分割する手法です。

• ボロノイ図との双対関係: 「領域」を示すボロノイ図とは裏表の関係にあり、「隣接関係」を可視化します。

• 幅広い分野での応用: CG、地形モデリング、科学シミュレーションなど、様々なハイテク分野で基盤技術として活用されています。

すぐにドロネー図を作成できるxGrapherを試してみてください！