樹形図とは？書き方の基本から応用例までを分かりやすく解説！

「確率の問題で樹形図を書きなさいと言われたけど、書き方がいまいち分からない…」
「場合の数を数え上げるときに、モレやダブリが多くて困っている…」

そんな悩みはありませんか？樹形図（じゅけいず）は、起こりうる全てのパターンを枝分かれさせて書き出すことで、場合の数や確率を正確に、そして視覚的に分かりやすく整理できる非常に便利なツールです。

この記事では、樹形図の基本的な意味から、誰でも簡単に書けるようになるための3つのステップ、具体的な例題、さらにはビジネスシーンでの活用例まで、分かりやすく解説していきます。この記事を読めば、あなたも樹形図をマスターして、複雑な問題もスッキリ解決できるようになるでしょう。

2025年9月12日2025年9月12日

樹形図を書くメリット

樹形図を使うことで、具体的にどのようなメリットがあるのでしょうか。主に以下の3点が挙げられます。

モレやダブリがなくなる: 起こりうる場合を一つずつ枝分かれさせて書き出していくため、「数え忘れていた！」といったモレや、「同じものを2回数えていた！」というダブリを防ぐことができます。これにより、場合の数や確率を正確に求めることができます。
思考が整理される: 問題の構造が木の枝のように視覚化されるため、複雑な条件が絡み合う問題でも、頭の中がスッキリ整理されます。どのようなパターンがあるのかを一目で把握できるのが大きな強みです。
他の人にも説明しやすい: 図として書き出されているため、自分がどのように考えてその結論に至ったのかを、他の人に分かりやすく伝えることができます。議論やプレゼンテーションの場でも役立ちます。

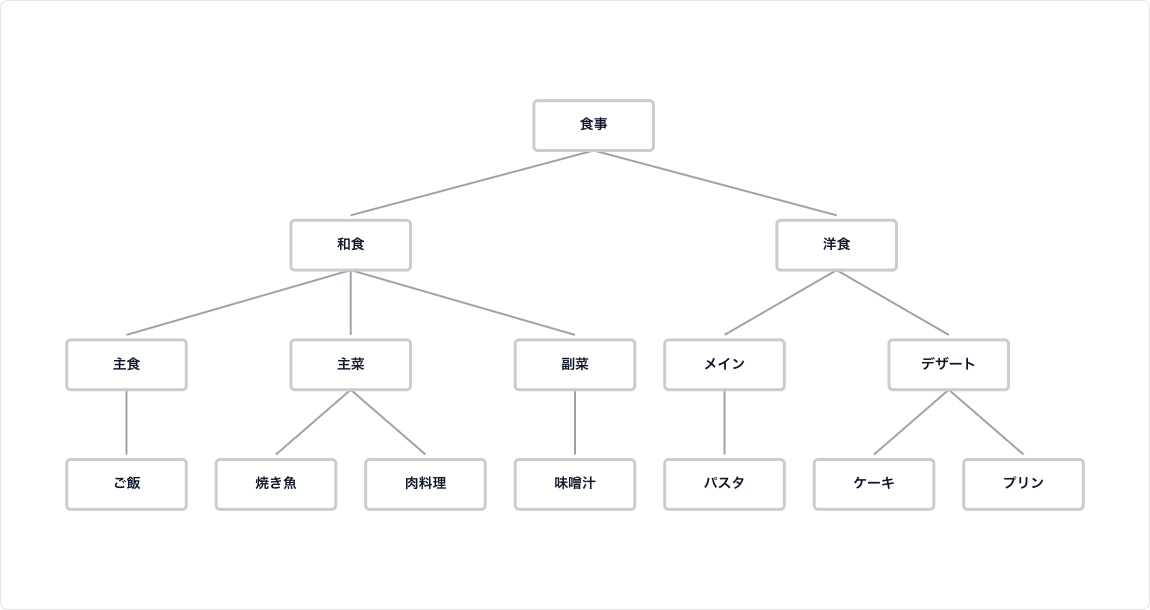
【基本】樹形図の書き方3ステップ

樹形図の書き方はとてもシンプルです。以下の3つのステップを意識すれば、誰でも簡単に書き始めることができます。

ステップ1：最初の状態（起点）を決める
まず、何についてのパターンを数え上げるのかを明確にし、最初の状態（起点）を一番左に書きます。例えば、「コインを3回投げる」という問題であれば、1回目の操作が起点になります。

ステップ2：起こりうる場合を枝分かれさせる
次に、起点から起こりうる全ての選択肢を線で結び、枝分かれさせます。コイン投げであれば、「表」と「裏」の2つの枝ができます。このとき、同じ階層の事象は縦に並べて書くと見やすくなります。

ステップ3：全ての場合が終わるまで繰り返す
2回目の操作、3回目の操作…と、問題の条件が終わるまで枝分かれを繰り返していきます。3回コインを投げるなら、2回目、3回目とそれぞれ「表」と「裏」の枝を伸ばしていきます。全ての枝の先が出揃ったら、樹形図の完成です。

【例題で実践】樹形図の書き方

それでは、具体的な例題を使って樹形図の書き方を練習してみましょう。簡単なものから少しずつレベルアップしていきます。

例題1：コインの表裏

問題： 1枚のコインを3回投げるとき、表と裏の出方は全部で何通りありますか？

考え方：

起点: 1回目の試行を左端に書きます。
枝分かれ: 1回目から「表(H)」と「裏(T)」の枝を伸ばします。
繰り返し: 2回目、3回目も同様に、それぞれの結果から「表(H)」と「裏(T)」の枝を伸ばします。

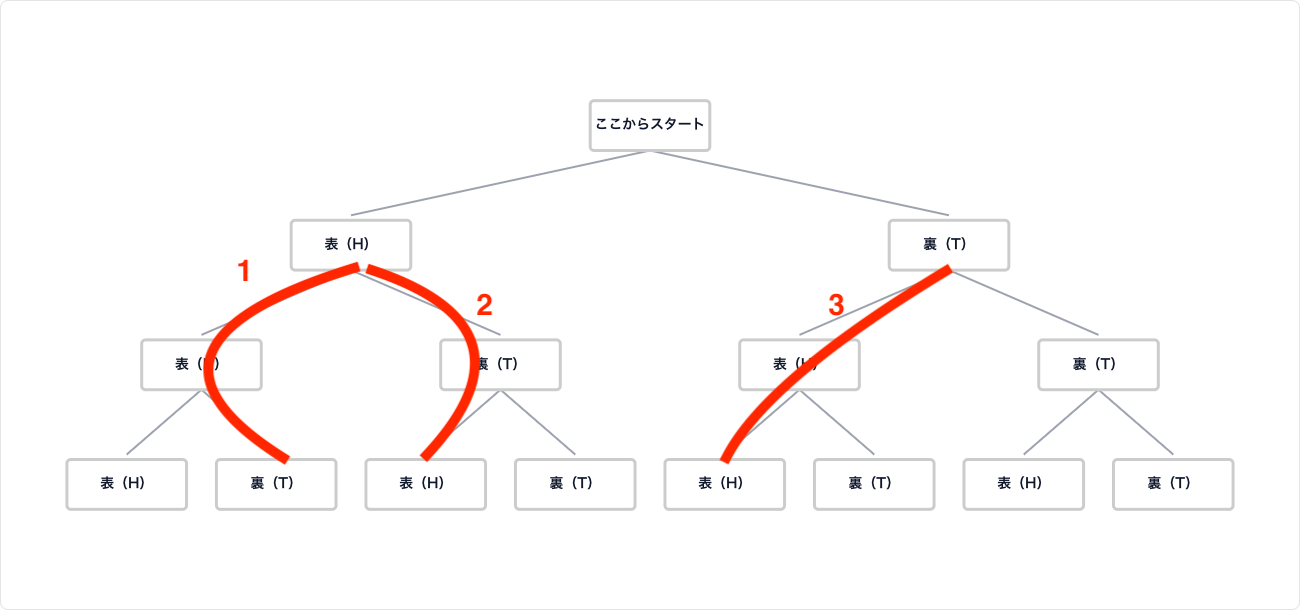
樹形図：

答え：
樹形図の右端の枝の数を数えると、8通りあることが分かります。
このように書き出すことで、「表が2回、裏が1回出るのは何通り？」といった問いにも、「HHT, HTH, THH の3通り」とすぐに答えることができます。

例題2：大小2つのサイコロ

問題： 大小2つのサイコロを同時に投げるとき、目の出方は全部で何通りありますか？

考え方：
大きなサイコロの目を起点（1〜6）とし、それぞれの場合について小さなサイコロの目（1〜6）がどう出るかを枝分かれさせていきます。

樹形図：

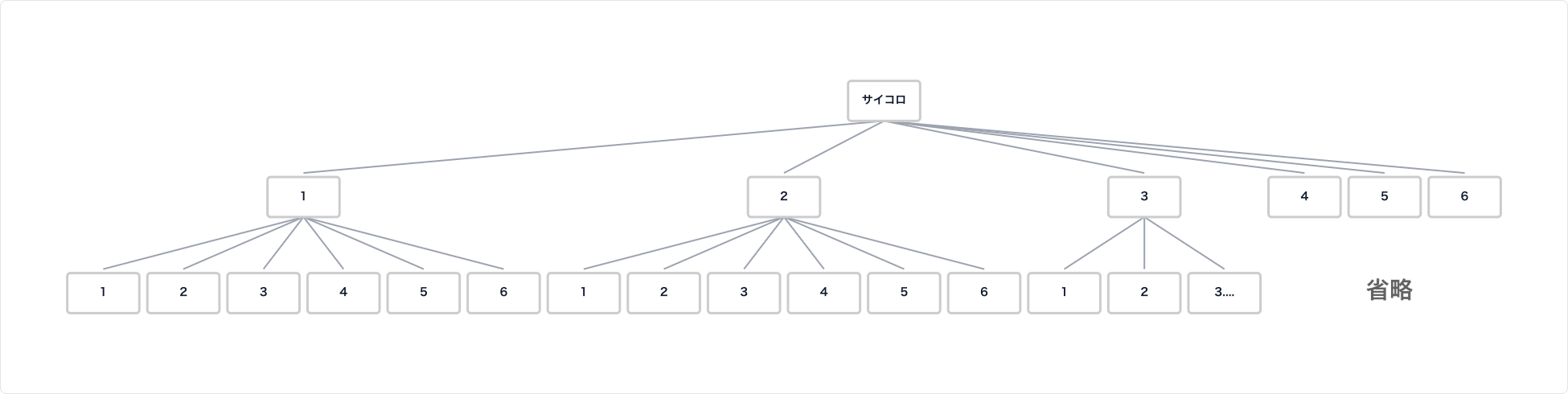
答え：
大きなサイコロの目が1の場合に6通り、2の場合に6通り…と続いていくので、全部で 6 × 6 = 36通り となります。
「目の和が5になるのは？」といった問題も、(1,4), (2,3), (3,2), (4,1) の4通りであると、樹形図から簡単に探し出すことができます。

例題3：カードの並べ方（順列）

問題： 1, 2, 3 の3枚のカードを並べて3桁の整数を作るとき、全部で何通りの整数ができますか？

考え方：
百の位、十の位、一の位を順番に決めていきます。一度使ったカードは使えないのがポイントです。

百の位: 1, 2, 3 のいずれかなので、3つの枝から始まります。
十の位: 百の位で使ったカード以外の2枚のカードが選択肢になります。
一の位: 百の位、十の位で使ったカード以外の最後の1枚が決まります。

樹形図：

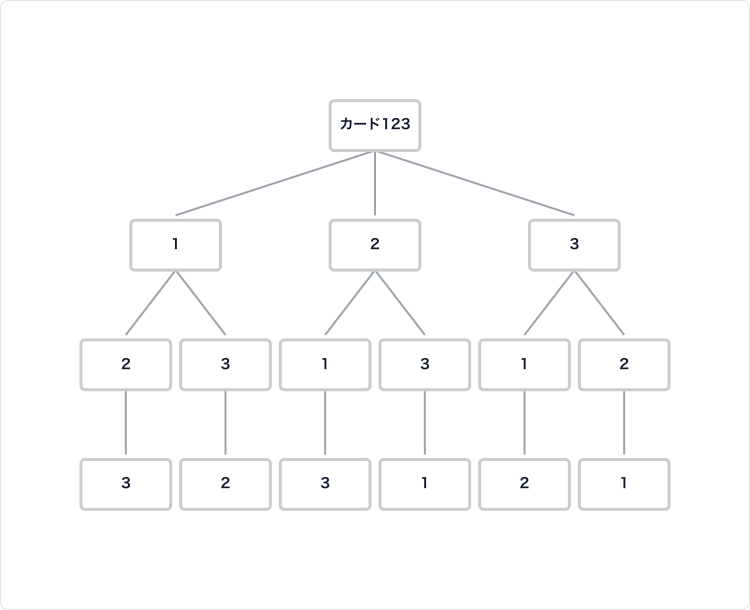
答え：
樹形図から、3 × 2 × 1 = 6通り の整数が作れることが分かります。

樹形図の応用｜ビジネスシーンでの活用例

樹形図の考え方は、確率や場合の数の問題だけでなく、ビジネスの世界でも広く応用されています。代表的なものがロジックツリーや決定木（デシジョンツリー）です。

ロジックツリー:
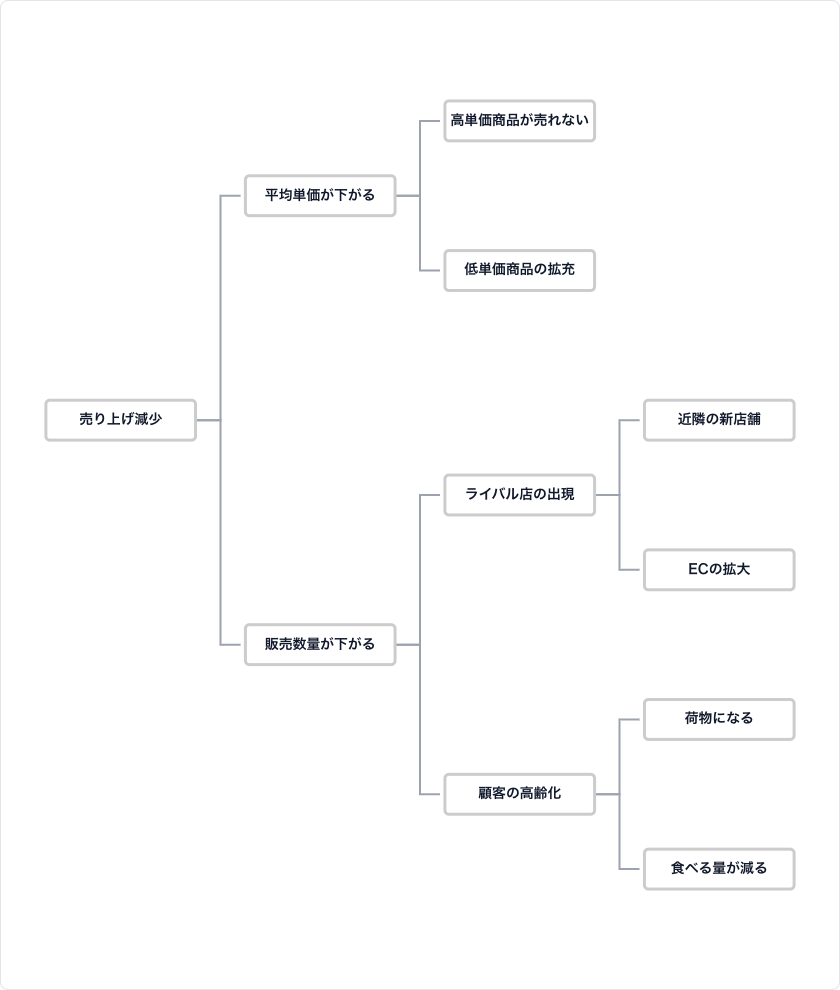
複雑な問題を大きな要素から小さな要素へと分解し、原因や解決策をMECE（ミーシー：モレなく、ダブりなく）に整理する際に使われます。「売上が下がっている」という問題に対して、「顧客数の減少」「客単価の減少」と分解し、さらにその原因を深掘りしていくような使い方をします。
決定木（デシジョンツリー）:
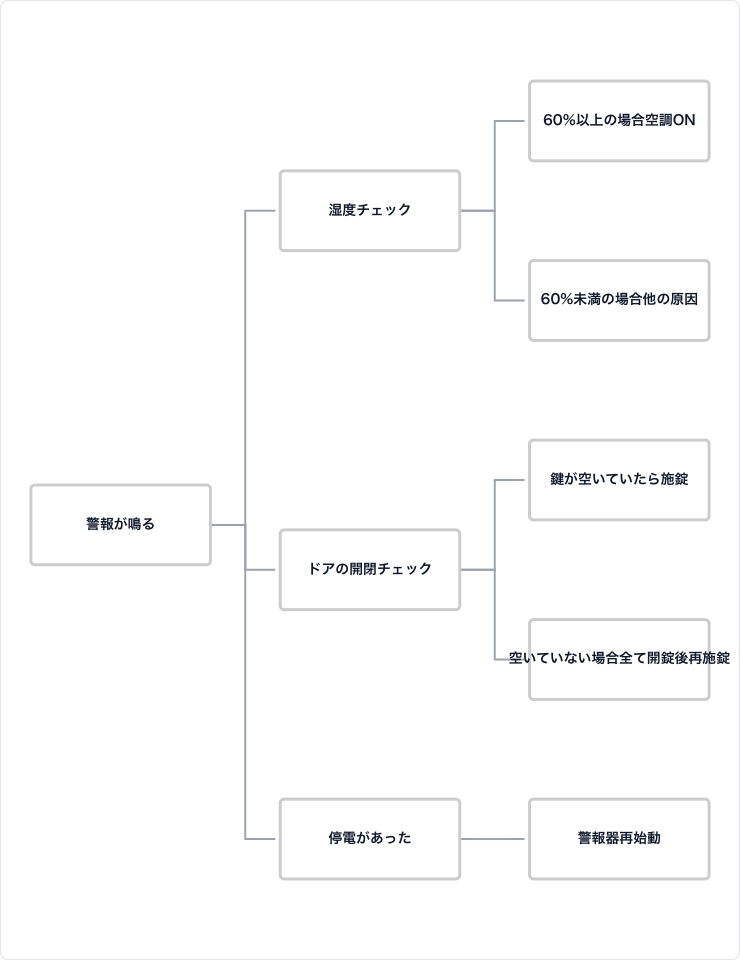
ある意思決定を行う際に、選択肢とその結果、不確実な事象などを樹形図で表し、最適な選択肢を見つけ出すために使われます。例えば、「新商品を発売すべきか？」という問いに対し、「発売する」「発売しない」の選択肢から、それぞれの成功/失敗の確率と利益を考慮して、期待値を計算するのに役立ちます。

[ロジックツリーのイメージ]

[決定木（デシジョンツリー）のイメージ]

手書きはもう古い？オンラインツールで樹形図を簡単作成

これまで見てきたように、樹形図は非常に便利ですが、場合の数が多くなると手書きではスペースが足りなくなったり、線がごちゃごちゃして見づらくなったりすることがあります。また、ビジネスで使うロジックツリーなどは、見た目の綺麗さや共有のしやすさも重要になります。

そこでおすすめなのが、オンラインのグラフ作成ツールです。
オンラインツールを使えば、以下のようなメリットがあります。

簡単操作: ドラッグ＆ドロップで直感的に枝を追加・編集できる。
自動でレイアウト調整: 要素を増やしても自動で綺麗に配置してくれる。
デザイン性が高い: 色や形を自由に変更でき、見やすい図が作れる。
共有・共同編集が楽: URL一つでチームメンバーと共有したり、一緒に編集したりできる。

私たちが提供する「xGrapher」も、こうした樹形図やロジックツリーをオンラインで手軽に作成できるツールの一つです。豊富なテンプレートを使えば、専門知識がなくてもすぐに美しいチャートを作成し始めることができます。複雑な確率の問題整理から、本格的なビジネス分析まで、幅広いシーンであなたの思考をサポートします。ぜひ一度、その使いやすさを体験してみてください。

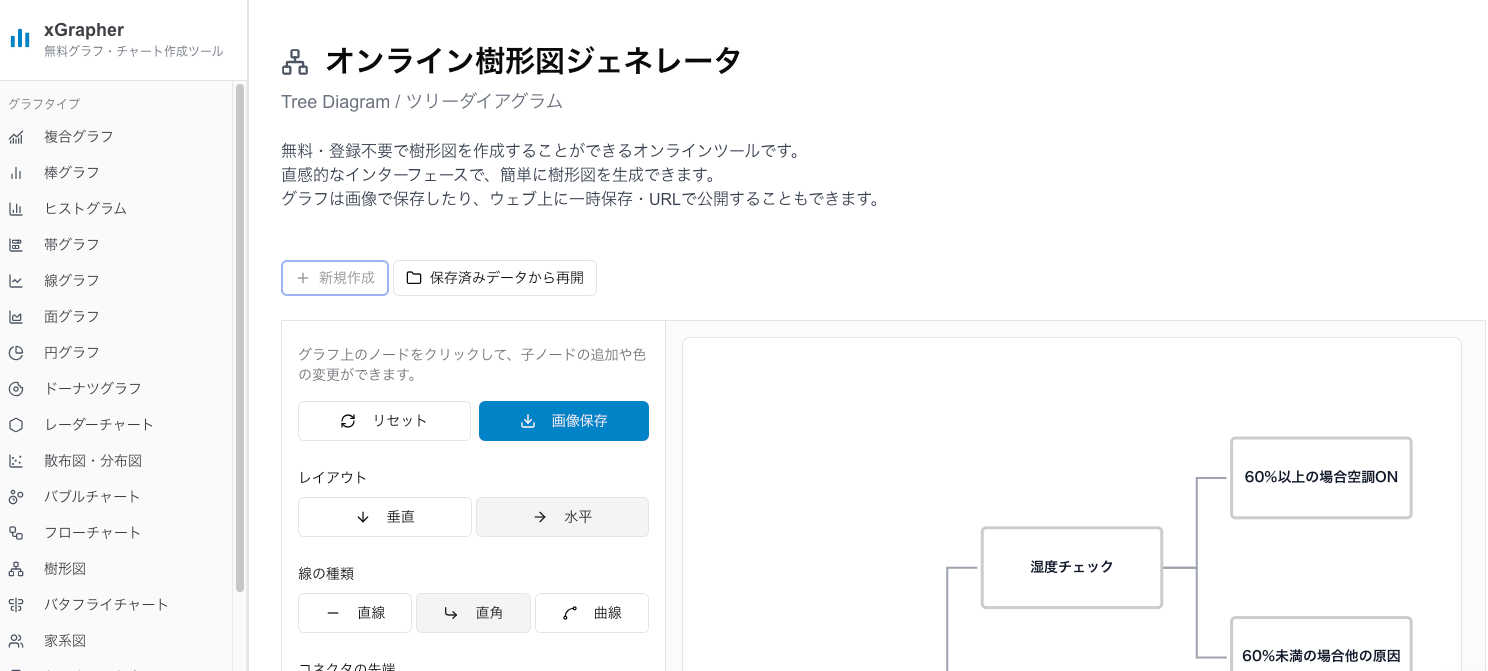
樹形図に関するよくある質問（Q&A）

Q1. 樹形図と順列・組み合わせの違いは何ですか？

A: これらは似ているようで役割が異なります。

樹形図: 起こりうる全てのパターンを「書き出すための図」です。思考を整理し、モレやダブリを防ぐためのツールと言えます。
順列: 「異なるものを順番に並べた」ときに何通りあるかを計算する方法です（例：ABC, ACB）。樹形図で書き出した結果のうち、順番が関係するものの総数を指します。
組み合わせ: 「異なるものからいくつか選んだ」ときに何通りあるかを計算する方法です（例：{A, B, C}から2つ選ぶ）。順番は問いません。

樹形図は、順列や組み合わせの考え方を視覚的に理解するのに役立ちます。

Q2. 樹形図を書くときに気をつけることはありますか？

A: はい、いくつかコツがあります。

階層を揃える: 1回目の操作、2回目の操作…と、同じ段階の事象は縦のラインが揃うように書くと、構造が分かりやすくなります。
十分なスペースを取る: 枝分かれしていくと横に広がっていくため、あらかじめ右側に十分なスペースを確保してから書き始めましょう。
同じ記号を使う: 例えばコインなら「表/裏」や「H/T」など、使う記号を統一すると見やすさが向上します。

これらの点を意識するだけで、格段に見やすい樹形図が書けるようになります。

Q3. 確率の問題は、すべて樹形図で解けますか？

A: いいえ、必ずしもすべての問題に適しているわけではありません。樹形図は、試行回数や選択肢が少ない場合には非常に有効ですが、サイコロを10回振るような、場合の数が膨大になる問題では、書き出すのが現実的ではありません。
そのような場合は、nCrやnPrといった計算式を使って解く方が効率的です。樹形図はあくまで「場合の数が多すぎない問題」を正確に解くための強力なツールと捉えましょう。