ピアソンの積率相関係数とは？公式や目安、データの可視化までわかりやすく解説

2025年11月17日2025年11月17日

「2つのデータの間に関係があるのかを知りたい」と思ったとき、最も一般的に使われる指標がピアソンの積率相関係数（Pearson correlation coefficient）です。単に「相関係数」と言った場合、通常はこのピアソンの積率相関係数を指します。

身長と体重、気温とアイスクリームの売上など、2つの変数が「直線的な関係」にあるかどうかを数値で表したものです。統計学の教科書で見ると難しそうに見えますが、基本を押さえればデータの分析に非常に役立つツールとなります。

この記事では、ピアソンの積率相関係数の意味や計算の仕組み、そしてなぜ計算するだけでなくグラフ（散布図）で見る必要があるのかについて、詳しく解説していきます。

この記事の内容（目次）

ピアソンの積率相関係数は、通常 $r$ という記号で表され、 $-1$ から $+1$ までの値をとります。この数値を見ることで、2つのデータがどのような関係にあるかがわかります。

「 $0.7$ なら強い？」「 $0.4$ だと弱いの？」という疑問を持つ方は多いでしょう。分野によって基準は異なりますが、一般的な目安については以下の記事で詳しく解説しています。自分のデータがどの程度当てはまるか確認してみてください。

少し専門的な話になりますが、ピアソンの積率相関係数 $r$ は以下の数式で求められます。

r = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^{n} (x_i - \bar{x})^2} \sqrt{\sum_{i=1}^{n} (y_i - \bar{y})^2}}

ここで、 $\bar{x}$ と $\bar{y}$ はそれぞれの変数の平均値です。
この式は、「共分散（2つの変数の偏差の積の平均）」を「それぞれの標準偏差の積」で割ったものと言い換えることができます。

なぜこのように複雑な式になるのか、具体的な計算手順はどうなっているのかを知りたい方は、以下の記事でステップごとに解説しています。

あわせて読みたい: 相関係数の計算方法を解説

ピアソンの積率相関係数は万能ではありません。実は、この手法を使うためにはデータがパラメトリック（正規分布に従っている）であり、かつ線形（直線）の関係であることが前提となります。

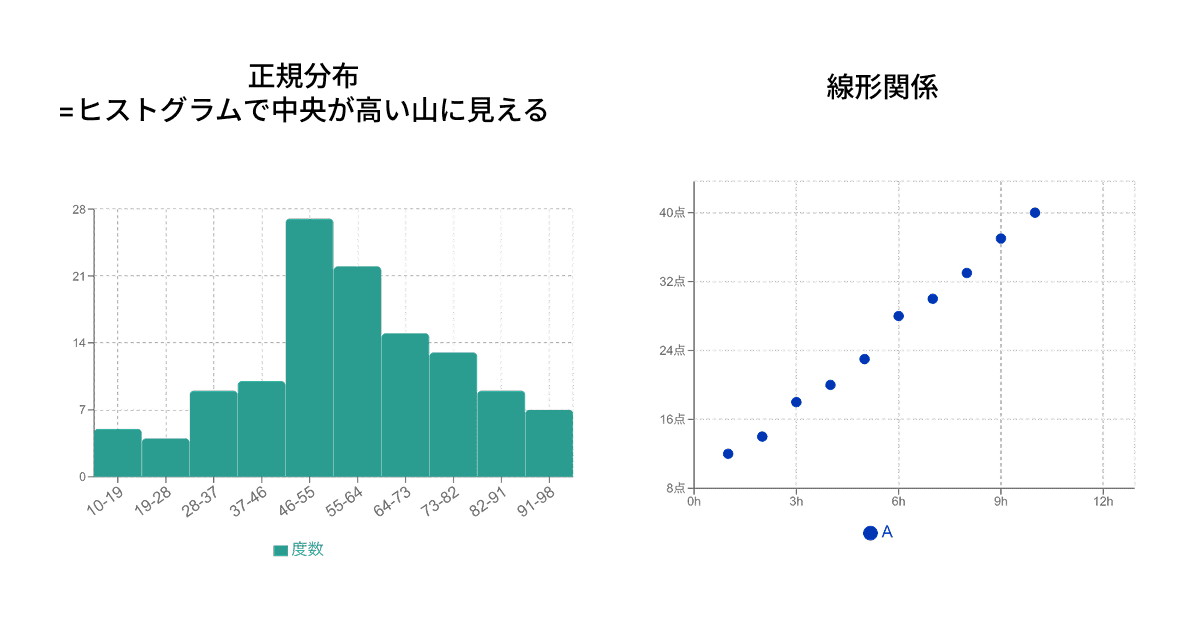
もし、データが正規分布していない場合や、順位データ（ランキングなど）を扱いたい場合は、ピアソンではなく別の相関係数を使う必要があります。

データが正規分布に従わない場合（ノンパラメトリックなデータ）は、順位に基づいた相関係数を使用します。

ここが最も重要なポイントです。相関係数 $r$ の値だけを見て結論を出してはいけません。

例えば、「外れ値（極端な値）」が一つあるだけで、本当は相関がないのに $r$ が高く出たり、逆に相関があるのにrが低くなったりすることがあります。必ず散布図（Scatter Plot）を作成して、目で見てデータの形を確認しましょう。

当サイト xGrapher では、ブラウザ上でデータを入力（またはExcelからコピペ）するだけで、美しいグラフを即座に作成できます。

基本的な相関を確認する:
2変数の関係を見るなら、まずは基本の散布図を作成しましょう。

👉 xGrapherで散布図（Scatter Plot）を作成する
3つの要素が絡む場合:
もし3つ目の変数（要素の大きさや、Z軸）がある場合は、バブルチャートや3D散布図が有効です。

👉 バブルチャート（Bubble Chart）を作成する

👉 3D散布図（XYZ Plot）を作成する